Druckumformen: Freiformen

Die Definition für das Freiformen nach DIN 8583-3 lautet:

Druckumformen mit nicht oder nur teilweise die Form eines Werkstückes enthaltenden, gegeneinander bewegten Werkzeugen. Die Werkstückform entsteht dabei durch freie oder festgelegte Relativbewegung zwischen Werkzeug und Werkstück (kinematische Gestalterzeugung).

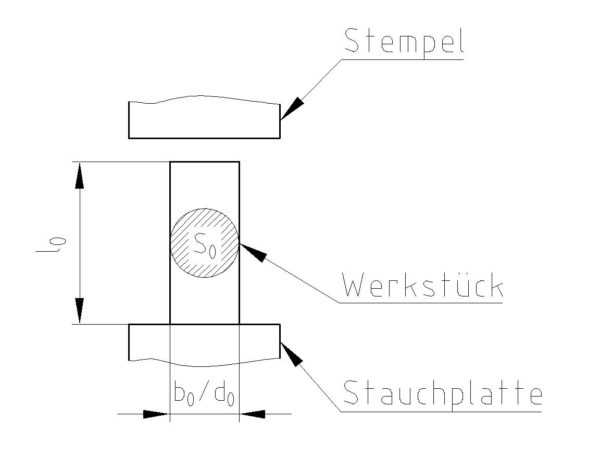
Stauchen

Die Definition für das Stauchen nach DIN 8583-3 lautet:

Freiformen, wobei eine Werkstückabmessung zwischen meist ebenen, parallelen Wirkflächen (Stauchbahnen) vermindert wird. Dabei ist die Stauchbahn stets größer als die gedrückte Werkstückfläche.

Vor dem Stauchen

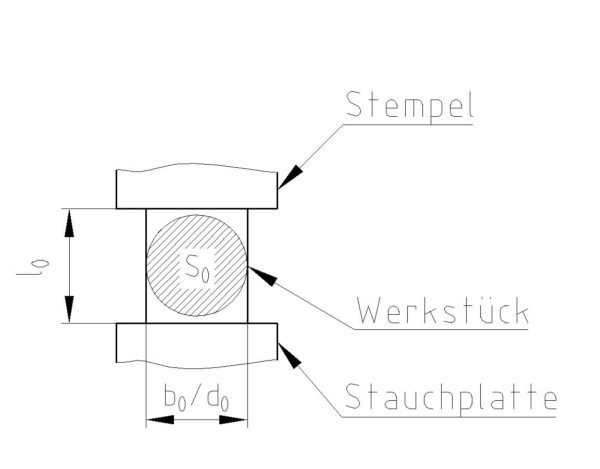
Nach dem Stauchen

Verwendete Formelzeichen

ε	[%]	bezogene Stauchung
η_f	[%]	Formänderungswirkungsgrad
η_M	[%]	Maschinenwirkungsgrad
µ		Reibwert
φ	[%]	Umformgrad
a	[Nmm/mm²]	bezogene spezifische Formänderungsarbeit
A₀	[mm²]	Ausgangsquerschnitt
A₁	[mm²]	umgeformter Querschnitt
b₀	[mm]	Ausgangsbreite
b₁	[mm]	Breite am Ende des Stauchens
d₀	[mm]	Ausgangsdurchmesser
d₁	[mm]	Durchmesser nach dem Umformen
F	[N]	Umformkraft
F_m	[N]	mittlere Stauchkraft
h₀	[mm]	Werkstückdicke vor der Bearbeitung
h₁	[mm]	Werkstückdicke nach der Bearbeitung
k_f0	[N/mm²]	Formänderungsfestigkeit vor der Umformung
k_fE	[N/mm²]	Formänderungsfestigkeit am Ende der Umformung
k_fm	[N/mm²]	mittlere Formänderungsfestigkeit
l	[mm]	Rohlingslänge
l₀	[mm]	Ausgangslänge
l₁	[mm]	Länge am Ende des Stauchens
P_a	[W]	Leistungsbedarf
s	Stauchverhältnis
V	[mm³]	an der Umformung beteiligtes Volumen
V₀	[mm³]	Volumen des Rohlings
V₁	[mm³]	Volumen nach dem Umformen
V_d	[mm³]	Volumen des Drahtabschnittes
V_k	[mm²]	Volumen der Kugel
W	[Nm]	Umformarbeit

Formeln

Rohlänge

$h_{0} = h_{1} \cdot \frac{{d_{1}}^{2}}{{d_{0}}^{2}} B e i r u n d e n W e r k s t ü c k e n h_{0} = \frac{h_{1} \cdot l_{1} \cdot b_{1}}{l_{0} \cdot b_{0}} B e i r e c h t e c k i g e n W e r k s t ü c k e n$

Stauchverhältnis

$s = \frac{h_{0}}{d_{0}} = \frac{h_{0}}{h_{1}} = \frac{l}{d_{0}}$

Stauchungsgrad

$φ = (\ln \frac{h_{0}}{h_{1}}) \cdot 100$

Mittlere Stauchkraft

$F_{m} = A_{1} \cdot k_{f m} \cdot (1 + \frac{1}{3} \cdot μ \cdot \frac{d_{1}}{h_{1}})$

Umformarbeit

$W = \frac{V \cdot k_{f m} \cdot φ}{η_{f}}$

Ausgangsdurchmesser

$d_{0} = \sqrt[3]{\frac{4 \cdot V}{π \cdot s}}$

Leistungsbedarf

$P_{a} = \frac{W \cdot n}{η M \cdot 60}$

Mittlere Formänderungsfestigkeit

$k_{f m} = \frac{k_{f 0} + k_{f E}}{2} k_{f m} = \frac{a}{φ}$

Volumen des Drahtabschnitts

$V_{d} = \frac{d^{2} \cdot π}{4} \cdot l$

Volumen der Kugel

$V_{K} = \frac{D^{3} \cdot π}{6}$ $k_{f e} ≙ k_{f l}$

Ausgangslänge

$l_{0} = \frac{{d_{1}}^{2}}{{d_{0}}^{2}} \cdot h_{1}$

bezogene Stauchung

$ε = \frac{h_{0} - h_{1}}{h_{1}} \cdot 100$

Schreibe einen Kommentar

2 Kommentare

Jan Wagner
31. Dezember 2022 / 17:51 Antworten
Hallo Nils,
Wie komme ich denn auf die Formel für den Ausgangsdurchmesser? Diese taucht in keiner meiner Formelsammlungen auf. Ich habe auch auf verschiedenen Wegen versucht sie selbst abzuleiten, was mir aber leider nicht gelingt. Vielleicht kannst du mir da weiterhelfen.
Gruß
Jan
- Nils
  7. Februar 2023 / 9:00 Antworten
  Hallo Jan,
  entschuldige bitte, dass ich jetzt erst antworte. Die Formel leitet sich aus dem Stauchverhältnis ab. Berücksichtigt man, dass beim Umformen eine Volumenkonstanz herrscht und setzt man z.B. die Dickenveränderung ins Verhältnis so gelangt man zu dieser Formel. Eine genaue Ableitung habe ich jetzt auch nicht parat.