Textliche Gleichungen

Im Alltag und der täglichen Berufspraxis ergeben sich immer wieder Aufgabenstellungen, welche auf „natürlicher“ Sprache formuliert sind. Dennoch erfordern diese oft eine mathematische Lösung.

Eine feste Formel gibt es zur Lösung solcher Problemstellungen leider nicht. Dennoch gibt es einige Hilfen, welche das allgemeine Vorgehen beschreiben.

1. Wonach wird gesucht?
2. Festlegen von Variablen für den gesuchten Wert und die Unbekannten.
3. Aufstellung der Gleichung.

Beispiel 1

Das Vierfache einer Zahl, verringert um 3, ergibt ebenso viel, als wenn das Dreifache der Zahl um 8 erhöht wird. Um welche Zahl geht es?

1. Wonach wird gesucht? Nach einer Zahl
2. Festlegen von Variablen für den gesuchten Wert und die Unbekannten. Wir nennen die gesuchte Zahl x
3. Aufstellung der Gleichung.

Das Vierfache einer Zahl… wir haben die Zahl x genannt. Also das Vierfache von x.

$4·x$

Verringert um 3… Also 3 weniger.

$4·x–3$

Ergibt ebenso viel… Ebenso viel also Gleich

$4·x–3=$

…als wenn das Dreifache der Zahl… (wieder der Bezug auf die unbekannte Zahl – also x)

$4·x–3=3·x$

…um 8 erhöht wird… Dieses mal 8 mehr, also +

$4·x–3=3·x+8$

Fertig ist die Gleichung! Jetzt brauchen wir nur noch lösen.

$$\begin{gathered} 4x–3=3x+8 |–8 \\ 4x–11=3x |–3x \\ x–11=0 |+11 \\ \underline{x=11} \end{gathered}$$

Probe: Das Ergebnis für x setzen wir in die Ursprungsgleichung ein.

$$\begin{gathered} 4·11–3 = 41 \\ 3·11+8 =41 \\ passt! \end{gathered}$$

Beispiel 2

Ein Maschinenbauer baut im zweiten Quartal eines Jahres durchschnittlich 7 Maschinen / Monat mehr, als der Monatsdurchschnitt im ersten Quartal beträgt. Wie viele Maschinen wurden im ersten Quartal pro Monat produziert, wenn im ersten Halbjahr insgesamt 357 Maschinen gebaut wurden?

1. Wonach wird gesucht? Nach der Anzahl von Maschinen / Monat
2. Festlegen von Variablen für den gesuchten Wert und die Unbekannten. x = Maschinen / Monat
3. Aufstellung der Gleichung.

Wir haben x (Maschinen / Monat) im ersten Quartal. Ein Quartal hat 3 Monate. Also 3x

$3x$

Im zweiten Quartal haben wir logischerweise wieder 3 Monate. Doch hier werden 7 Maschinen / Monat mehr gebaut. Wir erinnern uns x = Maschinen / Monat. Also addieren wir die 7 zu x und nehmen das Ganze mal 3, da wir ja 3 Monate in dem Quartal haben.

$3x + 3·(7+x)$

Insgesamt werden 357 Maschinen in dem Halbjahr gebaut. Wir nehmen also das erste Quartel und das zweite Quartal und erhalten das gesamte Halbjahr.

$3x + 3·(7+x)=357$

Fertig ist die Gleichung. Nun noch ausrechnen.

$$\begin{gathered} 3x+3·(7+x)=357 |ausmultiplizieren \\ 3x+3x+21=357 |zusammenfassen \\ 6x+21=357 |–21 \\ 6x=336 |÷6 \\ \underline{x=56} \end{gathered}$$

Beispiel 3

Zwei Brüder sind 21 und 29 Jahre alt. Vor wie vielen Jahren war der ältere Bruder dreimal so alt wie der jüngere?

1. Wonach wird gesucht? Nach der Anzahl der Jahre
2. Festlegen von Variablen für den gesuchten Wert und die Unbekannten. x = Jahre
3. Aufstellung der Gleichung.

Die Ausgangssituation sind die 21 und die 29 Jahre. Die Fragestellung lautet …vor viel Jahren? Das Ereignis liegt also in der Vergangenheit. Was bedeutet wir müssen Jahre abziehen.

$$\begin{gathered} 29–x \\ 23–x \end{gathered}$$

Außerdem wird danach gefragt vor wie viel Jahren der ältere Bruder dreimal so alt war. Also müssen wir das Alter des jüngeren mit 3 Multiplizieren um auf das 3-fache Alter und somit das Alter des Bruders zu dieser Zeit zu erhalten.

$$\begin{gathered} 29–x = 3·(21–x) |ausmultiplizieren \\ 29–x = 63–3x |–63 \\ –34–x =–3x |+3x \\ –34·2x = 0 |+34 \\ 2x =34 |÷2 \\ \underline{x=17} \end{gathered}$$

Beispiel 4

Mit wie viel cm³ 68 %igem Alkohol sind 630 cm³ mit 21%igem Alkoholgehalt zu mischen, damit 40%iger Alkohol entsteht?

1. Wonach wird gesucht? Die Menge Alkohol in cm³
2. Festlegen von Variablen für den gesuchten Wert und die Unbekannten. x = cm³
3. Aufstellung der Gleichung.

Wir haben einen festen Bestandteil in der Gleichung. Wir wissen, dass es 630 cm³ Flüssigkeit mit 21% Alkoholgehalt gibt.

$21·630$

Diesen Anteil mischen wir mit 68%igem Alkohol. Dieses mal kennen wir die Menge in cm³ nicht. Deswegen setzen wir unsere Variable x ein. Es wird danach gefragt wie viel von dem 68%igem und den 21%igem gemischt werden müssen um 40%igen zu erhalten. Darin steckt das der Alkoholgehalt des Ergebnisses 40% beträgt. Ein Ergebnis schreiben wir hinter einem Gleichheitszeichen. Wenn wir zwei Sachen zu einer Summe zusammensetzen müssen wir addieren.

$68 · x + 21· 630 = 40 (x + 630)$

Zu beachten ist, dass auch die 40% durch 100 geteilt werden müssen. Außerdem muss in dem Ergebnis der Gleichung auch die Menge vorkommen, da diese ja sonst unter den Tisch fallen würde und die Gleichung nicht aufgehen kann. In den beiden Summanden steht einmal x und einmal 630. Diese Werte sind die Summer der Mengen.

Jetzt lösen wir die Gleichung:

$$\begin{gathered} 68 · x + 21 · 630 = 40 (x + 630) |kürzen und ausmultiplizieren \\ 68x + 13230 = 40x + 25200 |–13230 \\ 68x = 40x + 11970 |–40x \\ 28x = 11970 |÷28 \\ \underline{x = 427,5} \end{gathered}$$

Bewegungsaufgaben

Bei Aufgaben, die mit Bewegung, Zeit und Geschwindigkeiten zu tun haben spricht man von sogenannten Bewegungsaufgaben. Diesen liegen die Beziehungen zu Grunde, welche durch die Physik definiert werden. Bei geradlinigen Bewegungen gilt die Beziehung:

$$\begin{gathered} Geschwindigkeit=\frac{Weg}{Zeit} \\ v=\frac{s}{t} \\ oder \\ Weg = Geschwindigkeit · Zeit \\ s = v · t \end{gathered}$$

Bei Bewegungsaufgaben muss immer überlegt werden, wo die jeweiligen Startpunkte sind und ab wann gestartet. Ob die die Bewegungen gleichzeitig stattfinden, ob die Geschwindigkeiten gleich sind oder unterschiedlich. Da dies ziemlich schnell sehr komplex werden kann, ist es ratsam bei solchen Aufgaben Bewegungsskizzen anzufertigen.

Grundsätzlich sind drei verschiedene Arten von Bewegungsaufgaben zu unterscheiden.

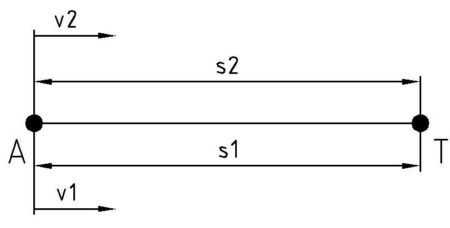
Typ 1

• Unterschiedliche Ausgangspunkte
• Bewegungsrichtung entgegengesetzt
• Startzeit gleichzeitig oder nacheinander
• unterschidliche oder gleiche Geschwindigkeit
• Gesamtweg = Summe der Einzelwege

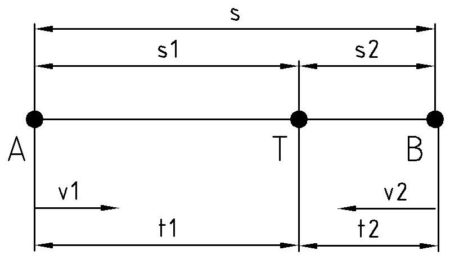
Typ 2

• Unterschiedliche Ausgangspunkte
• Bewegungsrichtung gleichgesinnt
• Geschwindigkeit verschieden
• Startzeit gleichzeitig oder nacheinander

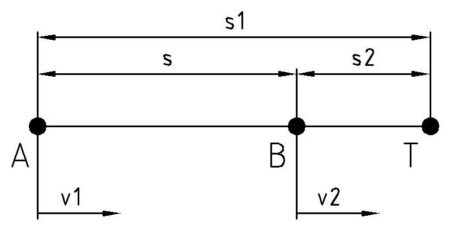
Typ 3

• Gleicher Ausgangspunkt
• Bewegungsrichtung gleichgesinnt
• Geschwindigkeit verschieden
• Startzeit nacheinander