Beanspruchung auf Zug

Wird ein Körper in Wirkrichtung seiner „Stabachse“ von äußeren Kräften gezogen, so spricht man von einer Zugbeanspruchung.

Zugversuch

Werkstoffe mit ausgeprägter Streckgrenze

Bei einem Zugversuch wird ein Stab beidseitig eingespannt und anschließend anschließend mit stetig wachsender Zugkraft auseinander gezogen. Zunächst dehnt sich der Stab nur elastisch (nicht dauerhaft). Dies bedeutet, dass er zur seinem Ursprungszustand zurückkehrt, wenn die Belastung aufgehört hat zu wirken. Wird der Stab über die Streckgrenze R_e hinaus belastet, so spricht man von einer plastischen (dauerhaften) Verformung. Diese findet bis zur Zugfestigkeit R_m ohne nennenswerte Einschnürung (Querschnittsverlust) statt. Wird die Zugfestigkeit überschritten steigt die Einschnürung an, bis der Stab schlussendlich reisst. Während des Versuchs wird stetig die Verlängerung ΔL der Probe gemessen. Aus der Zugkraft F und dem Querschnitt S₀ ergibt sich dann die Zugspannung σ_z.

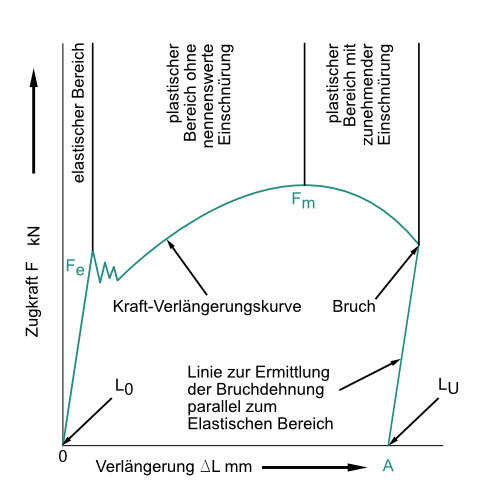
Laut dem Hooke´schen Gesetz steigt die Spannung im elastischen Bereich proportional zur Dehnung, deswegen bildet sich dort im Diagramm auch eine Gerade.

Werkstoffe ohne ausgeprägte Streckgrenze

Bei Werkstoffen ohne ausgeprägter Streckgrenze zeigt die Spannungs-Dehnungskurze keine Streckgrenze. Die Kurve steigt auch hier im elastischen Bereich wieder gerade an und geht dann nahezu übergangslos in den plastischen Bereich über. Um einen Ersatz für die Streckgrenze zu haben wird bei 0,2% Dehnung eine Parallele zur elastischen Linie gesetzt und an der Spannungs-Dehnungskurze die Spannung abgelesen. Diesen Wert nennt man R_p0,2. Dies ist nötig, da die Werte Streckgrenze und R_p0,2 sehr wichtig für die Festigkeitsberechnung sind.

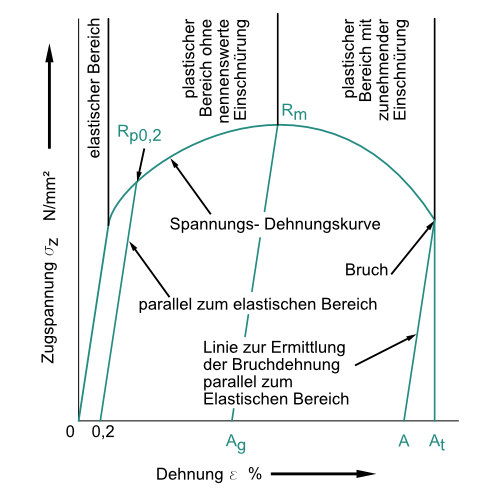
Formeln

Die folgenden Formelzeichen werden für die Formeln verwendet:

Aus dem Versuch lassen sich folgende Formeln ableiten:

Verlängerung

$\Delta L=L–L_0$

Zugspannung

${\sigma }_z=\frac{F}{A} bzw. {\sigma }_z=\frac{F}{S_0} = {\sigma }_z=E·\epsilon$

Druckspannung

${\sigma }_D=\frac{F}{A}$

Zugfestigkeit

$R_m=\frac{F_m}{S_0}$

Streckgrenze

$R_e=\frac{F_e}{S_0}$

Dehnung

$\epsilon =\frac{L–L_0}{L_0}·100\% = \epsilon =\frac{\Delta L}{L_0}·100\%$

Bruchdehnung

$A=\frac{L_U–L_0}{L_0}·100\%$

Brucheinschnürung

$Z=\frac{S_0–S_U}{S_0}·100\%$

Elastizitätsmodul

$E=\frac{{\sigma }_z}{\epsilon }·100\%$