Winkelfunktionen, Winkelarten

Winkelfunktionen

Es gibt drei nennenswerte Winkelfunktionen. Den Cotangens lasse ich bewusst außen vor, da sich auch Tangens umstellen und anwenden lässt.

Sinus

Rechtwinkliges Dreieck

$$\begin{gathered} \sin =\frac{Geg}{Hyp} \\ Hyp=\frac{Geg}{\sin } \\ Geg = \sin · Hyp \end{gathered}$$

Schiefwinkliges Dreieck

$$\begin{gathered} \frac{a}{b}=\frac{\sin {\displaystyle \alpha }}{\sin {\displaystyle \beta }} \\ \frac{b}{c}=\frac{\sin {\displaystyle \beta }}{\sin {\displaystyle \gamma }} \end{gathered}$$ $$\begin{gathered} a=\frac{b·\sin \alpha }{\sin \beta } = \frac{c·\sin \alpha }{\sin \gamma } \\ b=\frac{a·\sin \beta }{\sin \alpha } = \frac{c·\sin \beta }{\sin \gamma } \\ c=\frac{b·\sin \gamma }{\sin \beta } = \frac{a·\sin \gamma }{\sin \alpha } \end{gathered}$$

Cosinus

Rechtwinkliges Dreieck

$$\begin{gathered} \cos =\frac{Ank}{Hyp} \\ Hyp=\frac{Ank}{\cos } \\ Ank=\cos ·Hyp \end{gathered}$$

Schiefwinkliges Dreieck

Die Nutzung des Cosinus im schiefwinkligen Dreieck ist sinnvoll, wenn keine Winkel gegeben sind.

$$\begin{gathered} \cos \left(\alpha \right)=\frac{b^2+c^2–a^2}{2·b·c} \\ \cos \left(\beta \right)=\frac{a^2+c^2–b^2}{2·a·c} \\ \cos \left(\gamma \right)=\frac{a^2+b^2–c^2}{2·a·b} \end{gathered}$$

$$\begin{gathered} a^2=b^2+c^2–2bc \cos \alpha \\ {b}^2=a^2+c^2–2ac \cos \beta \\ {c}^2=a^2+b^2–2ab \cos \gamma \end{gathered}$$

Tangens

$$\begin{gathered} \tan =\frac{Geg}{Ank} \\ Ank=\frac{Geg}{\tan } \\ Geg=\tan ·Ank \end{gathered}$$

Winkelarten

In der Mathematik wird zwischen vier verschiedenen Winkelarten unterschieden.

Scheitelwinkel / Gegenwinkel

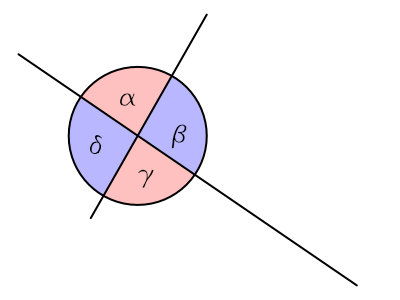
Der Scheitelwinkel ist der Winkel, der einem Winkel gegenüber liegt wenn sich zwei Geraden schneiden. Beide Winkel haben in diesem Fall den selben Wert. Im nachfolgenden Beispiel ist α der Scheitelwinkel von γ und β der Scheitelwinkel von δ. Also α = γ und β = δ

Nebenwinkel

Schneiden sich zwei Geraden wird der unmittelbar benachbarte Winkel als Nebenwinkel bezeichnet. Winkel und dessen Nebenwinkel ergeben in diesem Fall immer 180° Also  α + β = α + δ = γ + δ = γ + β = 180°

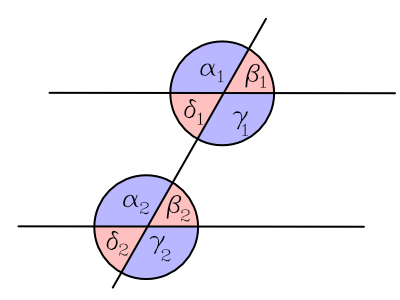
Stufenwinkel

Werden zwei parallele Geraden von einer weiteren Geraden geschnitten so bilden sich Stufenwinkel. also ist α₁ = α₂ usw.

Wechselwinkel

Als Wechselwinkel werden die Scheitelwinkel der zugehörigen Stufenwinkel bezeichnet. z.B. ist γ₁ der Wechselwinkel von α₂ da er der Scheitelwinkel von α₁ ist.