Exponentialfunktionen

Eine Exponentialfunktion ist eine Funktion mit der sich natürliche Wachstumsprozesse beschreiben lassen. Sie haben die Funktionsgleichung:

$y = a^x , a\in {\mathrm{ℝ}}_{+}^{*}$

oder auch

$$\begin{gathered} f\left(x\right) = s · b^x \\ f\left(t\right) = a · q^t \end{gathered}$$

Beispiel 1

Auf welchen Betrag wächst ein Kapital von 1000 € in sechs Jahren bei einer Verzinsung von 7 % an?

Lösung

Zunächst ermitteln wir den Zinsfaktor q Dieser wird auf Basis des Zinssatzes p ermittelt.

$$\begin{gathered} q = 1 + \frac{p}{100\%} \\ q = 1 + \frac{7\cancel{\%}}{100\cancel{\%}} \\ \underline{q = 1,07} \end{gathered}$$

Anschließend ermitteln wir das Endkapital nach einem Jahr.

$$\begin{gathered} K_n = K_0 · q^n \\ {K}_1 = 1000 € · 1,{07}^1 \\ \underline{K_1 = 1070 €} \end{gathered}$$

Für das zweite Jahr sieht es dann wie folgt aus:

$$\begin{gathered} K_2 = 1070€ · 1,{07}^1 \\ \underline{K_2 = 1144,9 €} \end{gathered}$$

Dies ließe sich jetzt bis zum sechsten Jahr so weiter rechnen, oder wir setzen direkt die 6 beim Anfangskapital ein.

$$\begin{gathered} K_6 = 1000 € · 1,{07}^6 \\ \underline{K_6 = 1500,73 €} \end{gathered}$$

Das lässt sich auch grafisch darstellen.

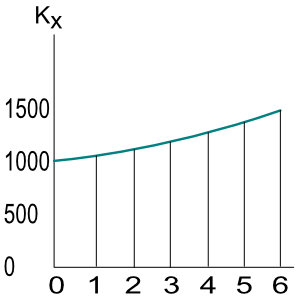
Das Kapital wächst über einen Zeitraum von 6 Jahren von 1000 € auf 1500,73 € an.

Wachstumsformel

$f\left(n\right) = s · {\left(1+\frac{p}{100}\right)}^n$

Zerfallformel / Schwund / Verlust

$f\left(n\right) = s · {\left(1–\frac{p}{100}\right)}^n$

Ist der Prozentsatz negativ so wird der Zinsfaktor < 0. In solchen Fällen spricht man nicht mehr von einem Wachstum sondern von Abschreibung bzw. Schwund / Verlust. Das Anfangskapital sinkt.

e-Funktion

Die e-Funktion ist eine besondere Form der Exponentialfunktionen mit der Basis e = 2,718281…. (Euler-Zahl).

Beispiel 1

Die γ-Strahlung von einem Radiumpräperats soll durch Bleiplatten abgeschirmt werden. Welche Plattendicke ist nötig um die Strahlung um die Hälfte zu reduzieren? Der Absorbtionskoeffizient von Blei beträgt ca. 0,513 cm^–1.

Zunächst stellen wir die Funktion auf.

$$\begin{gathered} f\left(x\right) = {\gamma }_{0 }· e^{p · x} \\ f\left(x\right) = {\gamma }_0 · e^{–0,513 · x} \end{gathered}$$

x ist der gesuchte Wert. γ₀ ist die Anfangsstrahlung. Bei Längen kann hier auch l₀ oder ähnliches stehen. Der Variablenname ist eigentlich frei wählbar. Die Basis bildet die Euler-Zahl  und der Exponent setzt sich aus dem eingesetzten Wert und der Variablen x zusammen. Der Wert ist in diesem Beispiel negativ eingesetzt, weil wir ja etwas reduzieren wollen, nämlich die Strahlung.

Als nächstes stellen wir zu x um. Für f(x) setzen wir nun γ₀/2 ein. Da wir ja die Plattendicke halbieren wollen.

$$\begin{gathered} \frac{{\gamma }_0}{2} = {\gamma }_0 · e^{–0,513 · x} |÷{\gamma }_0 \\ \frac{1}{2} = e^{–0,513 · x} |\ln (\log arithmus naturalis) \\ \ln \left(\frac{1}{2}\right) = –0,513 · x |÷(–0,513) \\ \frac{\ln \left({\displaystyle \frac{1}{2}}\right)}{–0,513}=x \\ \underline{x=1,351 cm} \end{gathered}$$

Bei einer Plattendicke von 1,351 cm beträgt die γ-Strahlung nur noch halb so viel.

Beispiel 3

Ein Wald hat einen Bestand von 50000 Festmetern. Bei einer angenommenen Wachstumsrate von 2,8%.

1. Aufstellen einer Gleichung
2. Wie viel Festmeter gibt es nach 40 Jahren?
3. Nach wie viel Jahren hat sich der Bestand verdoppelt?

a) Wir gehen wie im vorigen Beispiel vor. Nur, dass wir dieses mal den Startwert kennen.

$$\begin{gathered} f\left(x\right) = l_0 · e^{p · x} \\ f\left(x\right) = 50000 · e^{0,028 · x} \end{gathered}$$

b) Zunächst setzen wir die Zeit in die Gleichung ein, da hier alle Parameter bekannt sind, können wir die Gleichung direkt lösen.

$$\begin{gathered} f\left(40\right) = 50000 · e^{0,028 · 40} \\ \underline{f\left(40\right) = 153242,7 fm} \end{gathered}$$

c) Bei diesem Aufgabenteil ist die Anzahl der Jahre wieder unbekannt. Start und Endwert aber bekannt.

$$\begin{gathered} 100000 = 50000 · e^{0,028 · x} |÷50000 \\ 2 = e^{0,028 · x} |\ln \\ \ln \left(2\right) = 0,028 · x |÷0,028 \\ \frac{\ln \left(2\right)}{0,028} = x \\ \underline{x = 24 Jahre} \end{gathered}$$

Beispiel 4

Wasser wird auf Bakterienwachstum untersucht. Die Bakterienvermehrung wird beim Auszählen in bestimmten Zeitintervallen untersucht.

1. Wie viele Bakterien enthielt die Probe zu Beginn, wenn nach 1 Stunde 1800 Bakterien und nach 2 Stunden 2600 Bakterien gezählt wurden?
2. Wann hat sich die Bakterienanzahl verdoppelt?
3. wann beträgt sie 10000?

a) Zunächst stellen wir fest, dass wir zwei Endwerte haben. Wir haben jedoch keine Startwerte und auch die Wachstumsrate ist unbekannt. Deshalb werden zunächst zwei Gleichungen aufgestellt, dessen Werte bekannte sind.

$$\begin{gathered} 1800 = a · e^{1k} \\ 2600 = a · e^{2k} \end{gathered}$$

Doch was steht hier genau? 1800 und 2600 sind jeweils die Endergebnisse, diese stehen also alleine vor oder nach dem Gleich-Zeichen. a ist jeweils unser unbekannter Startwert. e die Euler-Zahl, 1 und 2 jeweils die betrachtete Zeit in Stunden und k die Wachstumsrate. Auch hier gilt wieder, dass die Variablennamen eigentlich frei wählbar sind (e ist in diesem Kontext die Euler-Zahl und keine Variable). Wir orientieren uns aber an der Gleichung des Aufgabenteils b.

Jetzt haben wir hier das Problem, dass sowohl die Wachstumsrate als auch der Startwert unbekannt sind um eine Variable zu eliminieren teilen wir die Gleichungen miteinander.

$$\begin{gathered} \begin{array}{c}1800 = a·e^k\\ 2600 = a·e^{2k}\end{array}\Rightarrow \frac{{\displaystyle \stackrel{9}{\cancel{1800}}}}{{\displaystyle \underset{13}{\cancel{2600}}}}=\frac{\cancel{a}·e^k}{\cancel{a}·e^{2k}} \\ \frac{9}{13}=\frac{e^k}{e^{2k}} \end{gathered}$$

Potenzen mit unterschiedlichen Exponenten und gleicher Basis werden dividiert indem die Exponenten subtrahiert werden!

$$\begin{gathered} \frac{9}{13}=e^{k–2k} \\ \frac{9}{13}=e^{–k} \end{gathered}$$

Um nach k aufzulösen verwenden wir die Umkehrfunktion der Euler-Zahl. Dies ist der logarithmus naturalis

$$\begin{gathered} \frac{9}{13}=e^{–k} |\ln \\ \ln \left(\frac{9}{13}\right)=–k \\ –0,37 =–k |·(–1) \\ 0,37 = k \end{gathered}$$

Jetzt haben wir die Wachstumsrate ermittelt und können diese in eine der Gleichungen einsetzen. Ich entscheide mich für die erste, da diese keinen Faktor für k enthält.

$$\begin{gathered} 1800 = a·e^{0,37} |÷e^{0,37} \\ \frac{1800}{e^{0,37}}=a \\ \underline{a=1243,3} \end{gathered}$$

Die Probe enthielt zu Beginn 1243,3 Bakterien.

b) Zunächst stellen wir wieder die Gleichung auf. Wir kennen den Zielwert 2486,6 was das doppelte des Startwertes 1243,3 beträgt. Wir kennen auch schon die Wachstumsrate k. Nur die Zeit ist unbekannt. Also stellen wir nach t um.

$$\begin{gathered} 2486,6=1243,3·e^{0,37·t} |÷1243,3 \\ 2 = e^{0,37·t} |\ln \\ \ln \left(2\right) = 0,37·t |÷0,37 \\ \frac{\ln \left(2\right)}{0,37}=t \\ \underline{t=1,87} \end{gathered}$$

Die Bakterien haben sich nach 1,87 Stunden verdoppelt.

c) Gleiche Vorgehensweise.

$$\begin{gathered} 10000=1243,3·e^{0,37·t} |÷1243,3 \\ 8,04 = e^{0,37·t} |\ln \\ \ln \left(8,04\right) = 0,37·t |÷0,37 \\ \frac{\ln (8,04)}{0,37}=t \\ \underline{t=5,63} \end{gathered}$$

Der Wert der Bakterien beträgt nach 5,63 Stunden 10000.