Es gibt diverse Welle-Nabe-Verbindungen. Die gebräuchlichsten seien hier aufgelistet:
Welle-Nabe-Verbindungen: Formschluss
Passfedern

Passfeder-Verbindungen sind Welle-Nabe-Verbindungen, die formschlüssig als reine Mitnehmerverbindungen arbeiten. Für stoßartige Belastungen ist diese Verbindung nicht geeignet, da es hier aufgrund der Stöße im schlimmsten Fall zur Abscherung kommen kann.
Passfedern gibt es nach DIN 6885 in verschiedenen Formen, wobei nicht alle davon regelmäßige Anwendung finden:
- A – rundstirnig
- B – geradstirnig
- C – rundstirnig mit 1 Bohrung für Halteschraube
- D – geradstirnig mit 1 Bohrung für Halteschraube
- E – rundstirnig mit 2 Bohrung für Halteschraube
- F – geradstirnig mit 2 Bohrung für Halteschraube
- G – geradstirnig mit 1 Bohrung für Halteschraube und Schrägung
- H – geradstirnig mit 2 Bohrung für Halteschraube und Schrägung
- J – geradstirnig mit 1 Bohrung für Spannhülse und Schrägung
Passfedern werden in Nuten für Passfedern eingesetzt. Diese werden meist für „Gleitsitz“, „Übergangssitz“ oder „festen Sitz“ mit Toleranzen versehen. Für die Oberflächen werden in der DIN keine gezielten Vorgaben gemacht.
| Sitzcharakter | Nutenbreite | Passungscharakter | |
| Welle | Nabe | ||
| beweglich | H9 | D10 | Gleitsitz |
| leicht montierbar | N9 | JS9 | Übergangssitz (auch leichter Sitz) |
| für wechselseitiges Drehmoment | P9 | P9 | Festsitz |
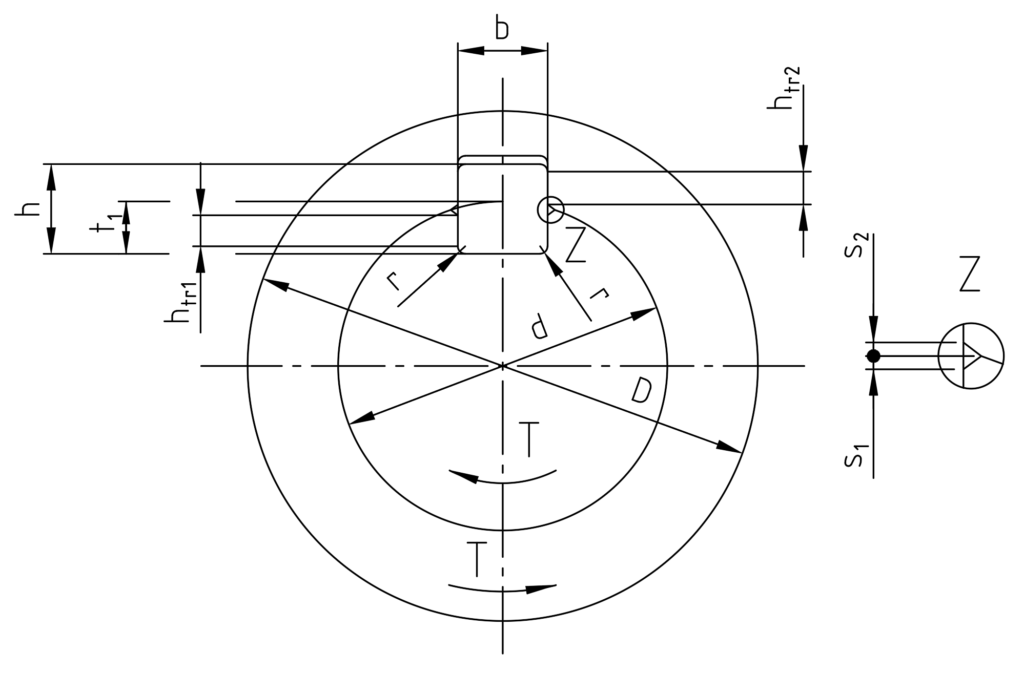
Berechnung von Passfedern
Formelzeichen
| Formelzeichen | Bezeichnung | Einheit |
| pmax | maximale Flächenpressung | N/mm² |
| pzul | zulässige Flächenpressung | N/mm² |
| Tmax | maximales Drehmoment | Nmm / Nm |
| Teq | äquivalentes Nennrehmoment | Nmm / Nm |
| Kλ | Lastverteilungsfaktor (siehe RM TB 12-2C) | oE |
| KR | Reibschlussfaktor (1 bei Spiel und Übergangspassung) | oE |
| Kt | technologischer Größeneinflussfaktor (siehe RM TB 3-11a,b) | oE |
| d | Wellendurchmesser | mm |
| D | Nabendurchmesser | mm |
| htr | tragende Nuttiefe | mm |
| ltr | tragende Passfederlänge | mm |
| l | Passfederlänge (siehe RM TB 12-2) | mm |
| b | Passfederbreite (siehe RM TB 12-2) | mm |
| h | PAssfederhöhe (siehe RM TB 12-2) | mm |
| n | Anzahl der Passfedern | oE |
| φ | Tragfaktor zur Berücksichtigung der Passfederanzahl n = 1 → φ = 1 n = 2 → φ = 0,75 bei peq, φ = 0,9 bei pmax | oE |
| fL | Lastspitzenhäufigkeitsfaktor (siehe RM TB 12-2d | oE |
| fS | Stützfaktor (siehe RM TB 12-2b) | oE |
| fH | Härteeinflussfaktor (siehe RM TB 12-2b) | oE |
| fW | Lastrichtungswechselfaktor (siehe RM TB 12-2e) | oE |
| Q | Durchmesserverhältnis | oE |
| qmax | Korrekturfaktor für Reibschluss | oE |
| Re | Streckgrenze | N/mm² |
Es gibt verschiedene Methoden zur Passfederberechnung. Wir werden hier nur die Methode B betrachten, bei der die Pressung genauer betrachtet wird. Methode A dient nur zum experimentellen Nachweis und Methode C darf nur bei einseitig wirkendem Torsionsmoment verwendet werden. Außerdem betrachten wir hier nur die Spiel, bzw. Übergangspassung, da diese der Regelfall sind.
In der Regel ist ein Nachweis der Passfeder nicht notwendig wenn das Durchmesserverhältnis QA = d / D < 0,6 ist.
Bei Passfedern wird in der Praxis der Nachweis gegen die Flächenpressung geführt. Zwar wird auch die Grundfläche der Passfeder auf Abscherung beansprucht, verwendet man aber Passfedern nach Norm ist die Grundfläche deutlich größer als die zu überprüfende Fläche der Flächenpressung. Deshalb wird darauf verzichtet.
Formeln
maximale Flächenpressung (statisch)
äquivalente Flächenpressung (dynamisch)
zulässige Flächenpressung
tragende Nuttiefe
tragende Passfederlänge (rundstirnig)
tragende Passfederlänge (geradstirnig)
Streckgrenze
Beispiel
Eine Passfeder (Typ A) aus C45E, mit einer Länge von 45 mm, soll ein Drehmoment von 230 Nm übertragen. Die Welle hat einen Durchmesser von 22 mm und wird statisch beansprucht.
Lösung:
1) Das Drehmoment kennen wir bereits. Es beträgt 230000 Nmm.
2) Den Lastverteilungsfaktor Kλ ermitteln wir mit ltr / d und lesen diesen aus dem Graphen ab.
Wert für Kλ
Ablesen aus dem Graph:
3) Als nächstes stellen wir fest, dass KR bei einer Übergangspassung 1 beträgt.
4) Nun ermitteln wir die tragende Nuttiefe htr. Eine Fase ist hier nicht gegeben also lassen wir den Wert auf 0
5) ltr haben wir bereits ermittelt und die Anzahl der Passfedern n ist 1 womit φ ebenfalls 1 ist.
6) Jetzt berechnen wir die zulässige Flächenpressung.
Die zulässige Flächenpressung:
Schauen wir uns den Vergleich an:
7) Wir halten fest pmax ist geringer als pzul somit ist die Passfeder ausreichend dimensioniert.

das ist aber toll
freut mich, dass es dir gefällt. 🙂