Die Berechnung von Kontrollmaßen ist ein typischer Anwendungsfall für Winkelfunktionen, mit der Erschwernis, dass die zu errechnenden Dreiecke nicht immer offensichtlich sind. Um diese Dreiecke leichter zu finden, gibt es jedoch einige Ansatzpunkte und Tipps.
Oft führt der Weg zur Berechnung des Kontrollmaßes über die Messwalzen. Der Durchmesser der Messwalzen sollte eigentlich immer bekannt sein. Somit kennen wir auch den Radius, also auch die Strecke zwischen dem Mittelpunkt der Messwalze zu der anliegenden Fläche.
Beispiel 1
Gegeben sind der Winkel α, der Durchmesser D und das Maß b. Errechnet werden soll K.
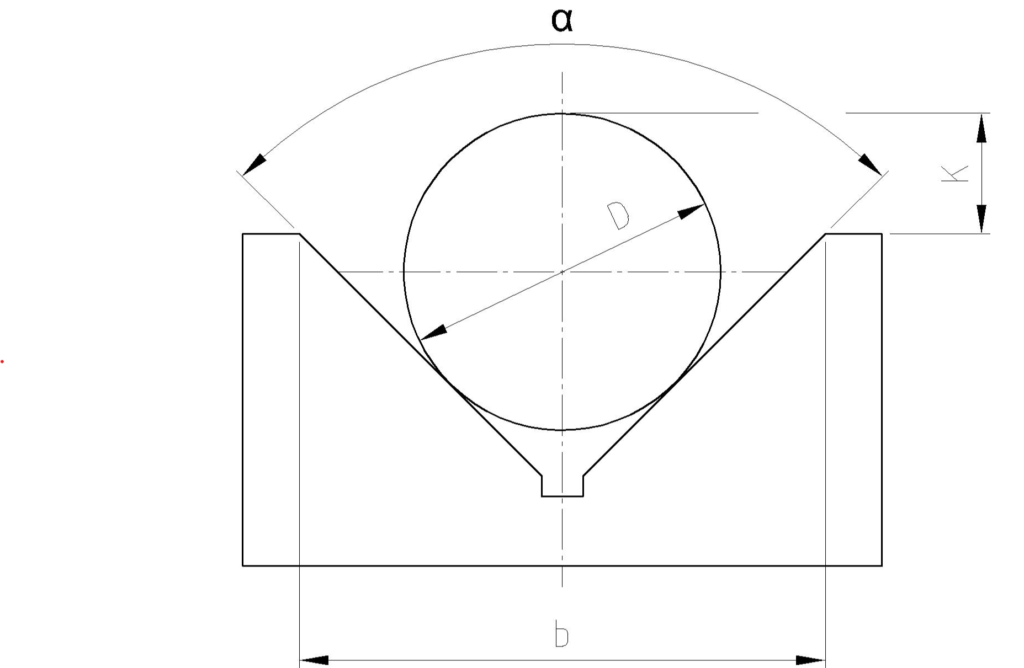
Die Problematik ist nun mit den angegebenen werten auf die horizontale Körperkante des Prismas zu kommen. Die erste wichtige Erkenntnis wurde bereits genannt – Der Radius. Die Hälfte vom Durchmesser D ist der Radius R. trägt man diesen nun lotrecht zum Prisma ab und verlängert die Linie des Prismas erhalten wir ein rechtwinkliges Dreieck. Der Winkel ist α/2 da wir ja genau bis zur Mittelachse der Walze gehen und R dient uns als Gegenkathete.
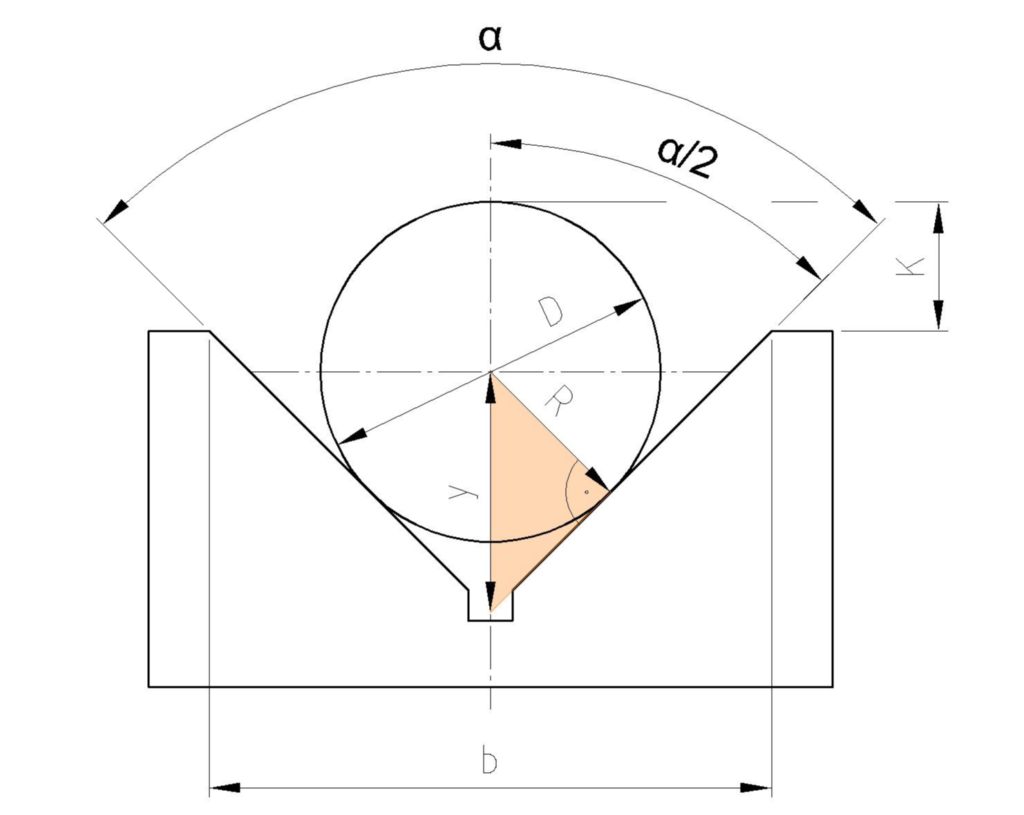
Dadurch erhalten wir das Maß y, welches uns zwar erst einmal nicht viel bringt, aber immerhin haben wir nun ein Höhenmaß mit direktem Bezug zum Prisma, nämlich der gedachten weiterführenden Linie der Schräge. Jetzt brauchen wir nur noch ein Dreieck bis zur Horizontalen.
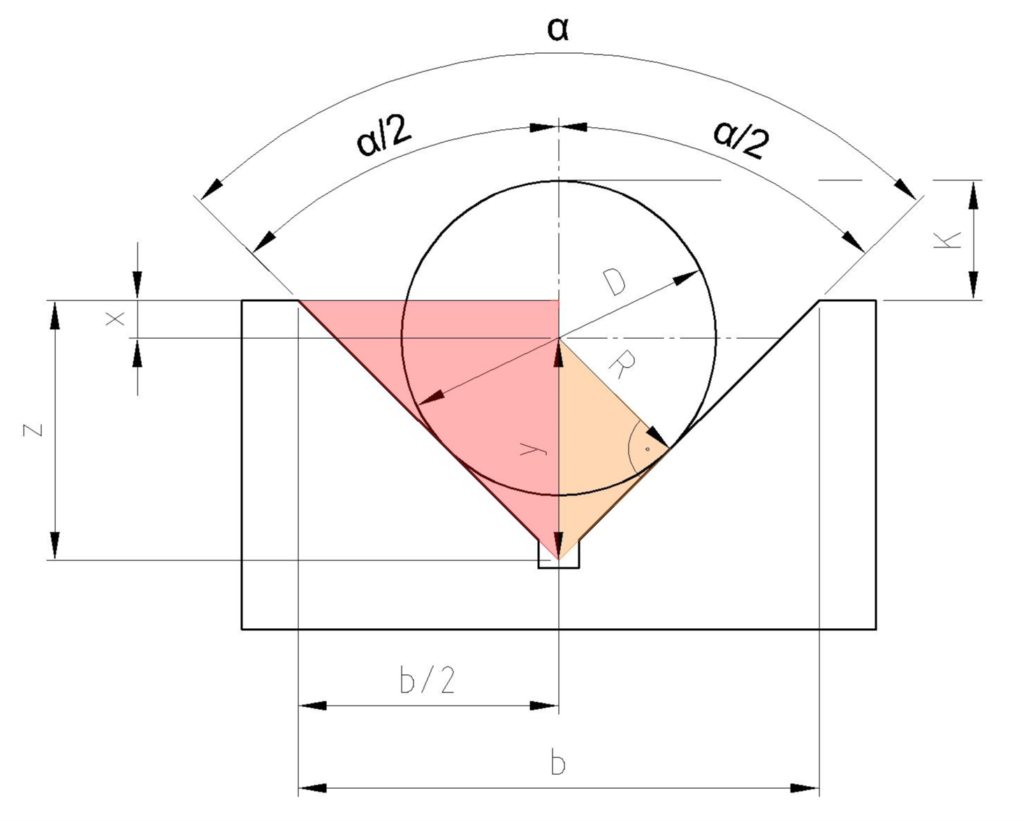
Auch hier ist wieder α/2 gegeben sowie b/2 als Gegenkathete. Jetzt können wir das Maß z errechnen. Davon subtrahieren wir y und bekommen das Maß x. Nun brauchen wir nur noch x vom Radius R abziehen und erhalten K.
Beispiel 2
Gegeben sind die Länge l, der Durchmesser d, der Winkel α und das Höhenmaß h. Errechnet werden soll K
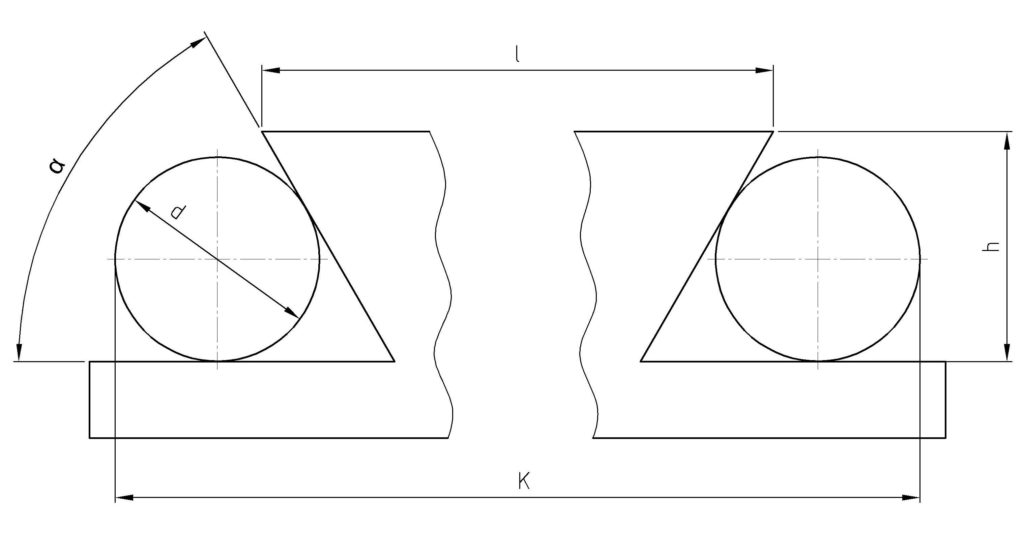
Auch hier finden sich wieder Dreiecke, die auf dem ersten Blick vielleicht nicht offensichtlich sind.
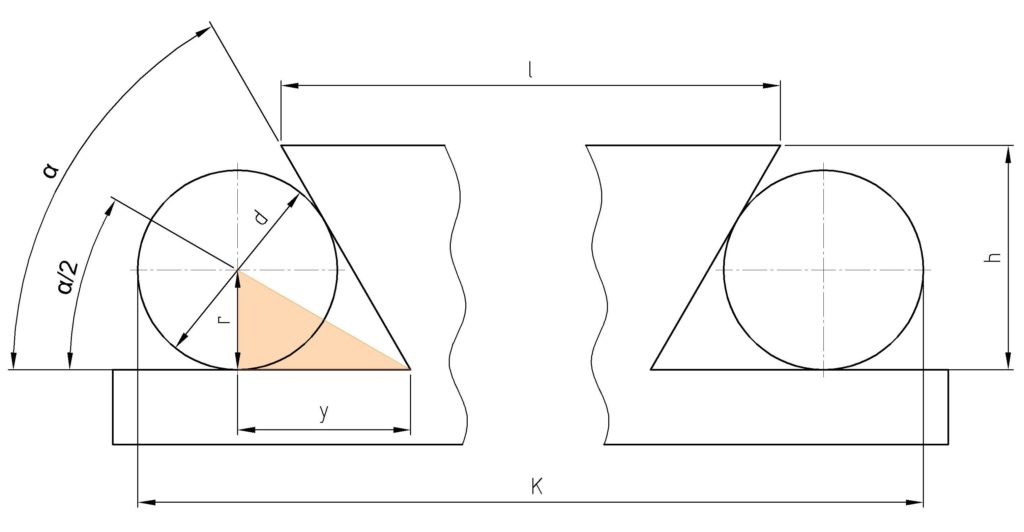
Das erste Dreieck führt uns zur Mittelachse. Wir haben den Winkel. Dieser Beträgt α/2, da die Mittelachse die Winkelhalbierende zum angegebenen Winkel bildet. Außerdem haben wir die Gegenkathete, diese ist der Radius der Messwalze. Aus diesem Dreieck errechnen wir das Maß y.
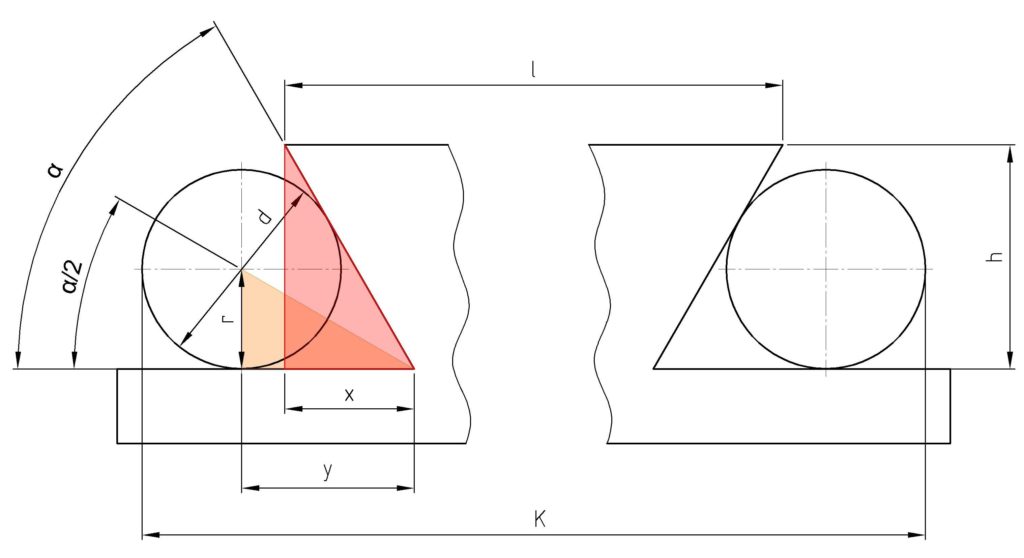
Das zweite Dreieck bildet sich aus der Höhe h der Schräge des Schwalbenschwanzes und dem Winkel α. Hier erhalten wir das Maß x.
Das Kontrollmaß K ergibt sich also wie folgt:
Beispiel 3
Hier wird ein Werkstück mit fest definierten Radien mit einem Winkelmesser geprüft werden. Dazu muss der Flankenwinkel α ermittelt werden.
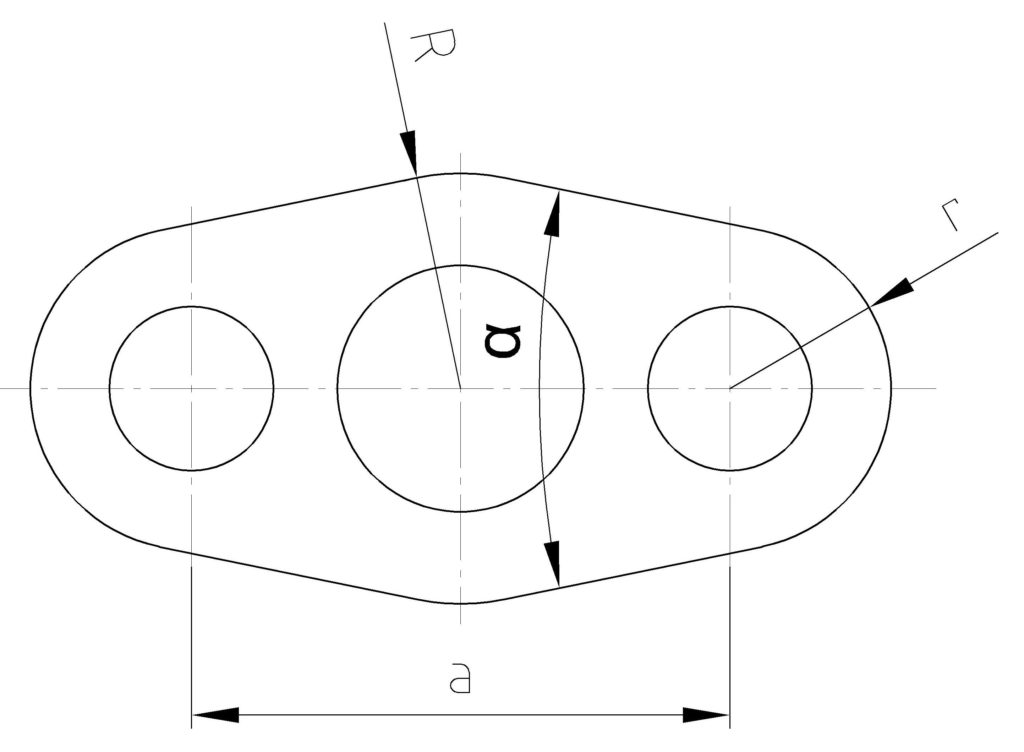
Zunächst einmal müssen wir ein Dreieck finden. Was machen wir im nächsten Schritt? Wir zeichnen Linien vom jeweiligen Kreismittelpunkt rechtwinklig auf die Tangente, welche die beiden Radien verbindet.
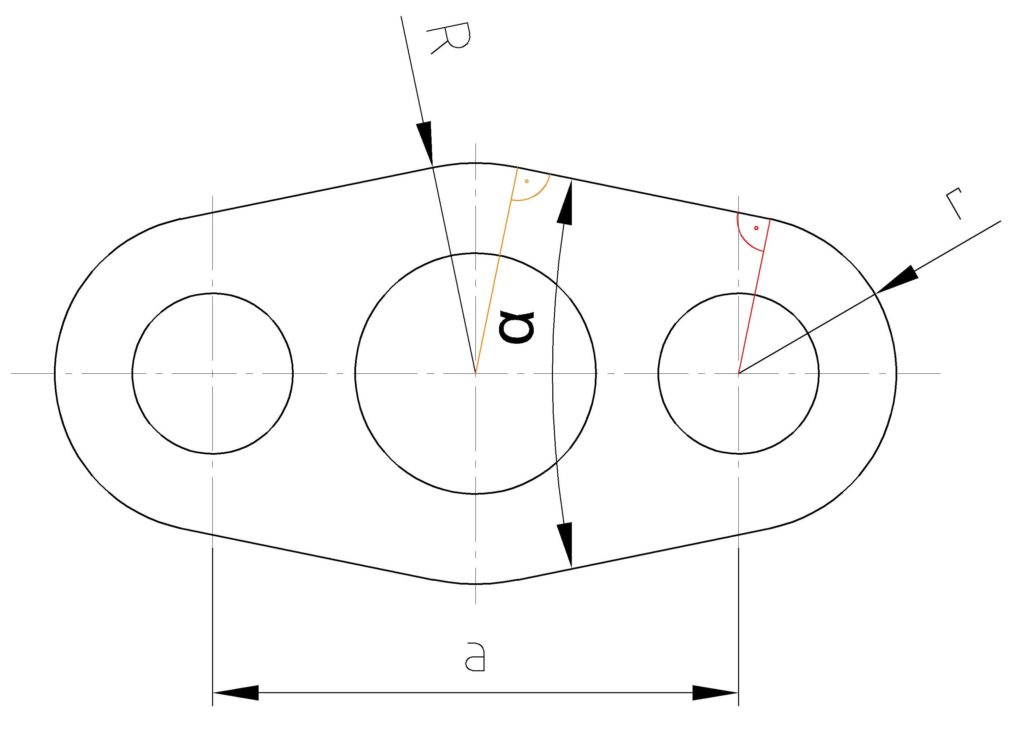
Diese Linien verbinden wir mit einer horizontalen Linie.
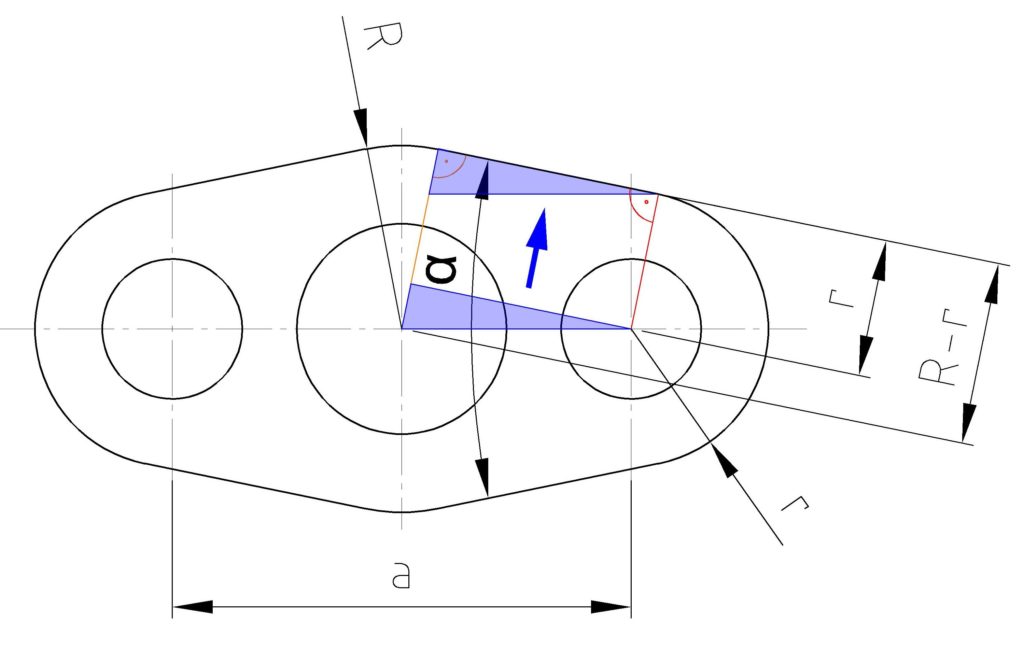
Wie kommen wir nun darauf? Das Maß a ist das einzige welches uns außer der Radien gegeben ist. Wir müssen also Dreiecke finden, wo wir das Maß benutzen können. Nicht immer ist das gleich offensichtlich.
Nun können wir also a/2 für die Ankathete einsetzen und R-r für die Gegenkathete.
