Einheitskreis

Winkelfunktionen im Einheitskreis

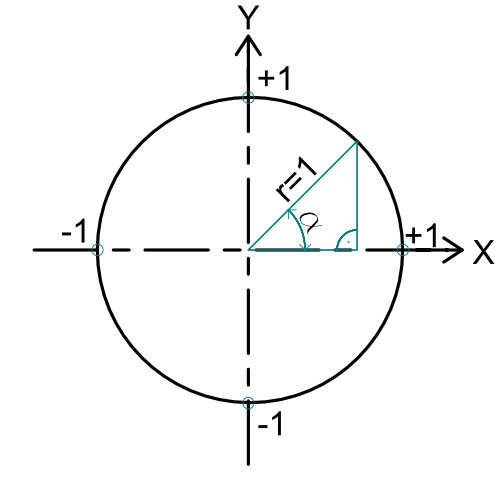
Der Einheitskreis ist ein Kreis, welcher einen Radius von 1 hat. Er dient zur Veranschaulichung der Winkelfunktionen.

Egal wo wir vom Mittelpunkt aus eine Linie auf den Kreis ziehen. Sie wird immer die Länge 1 haben. Das ist der Radius. ziehen wir nun von dem Punkt, wo die Linie auf den Kreis trifft eine lotrechte Linie auf die X-Achse erhalten wir ein rechtwinkliges Dreieck. Genau diesen Umstand können wir uns zu Nutze machen um die Winkelfunktionen daraus abzuleiten.

Bezogen auf den Einheitskreis können wir die Winkelfunktionen also wie folgt beschreiben:

Sinus

Der Wert den y hat, wo die Linie auf den Kreis trifft geteilt durch 1 ist der Wert y.

$\sin \left(\alpha \right)=\frac{GEG}{HYP} = \sin \left(\alpha \right)=\frac{y}{1}=y$

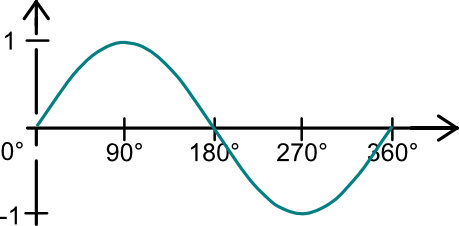
Cosinus

Der Wert den x hat, wo die Linie auf den Kreis trifft geteilt durch 1 ist der Wert x.

$\cos \left(\alpha \right)=\frac{ANK}{HYP} = \cos \left(\alpha \right)=\frac{x}{1}=x$

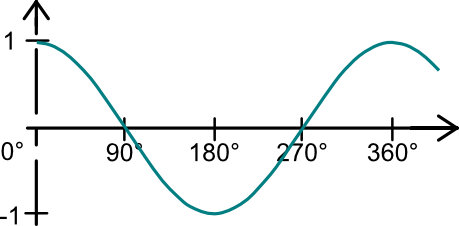
Nehmen wir also nun einen Kreis mit detaillierterer Skala, so könnten wir anhand der Werte in X und Y Richtung die Winkel in ° ablesen oder die Cosinus bzw. Sinus Werte, wenn uns andersherum der Winkel bekannt ist.

Es ergibt sich zwischen Sinus und Cosinus noch eine weitere Beziehung daraus. Nämlich

$1=\sin (\alpha {)}^{2 }+ \cos (\alpha {)}^2$

Egal welchen Winkel wir für α einsetzen. Das Ergebnis wird immer 1 sein.

Beispiel

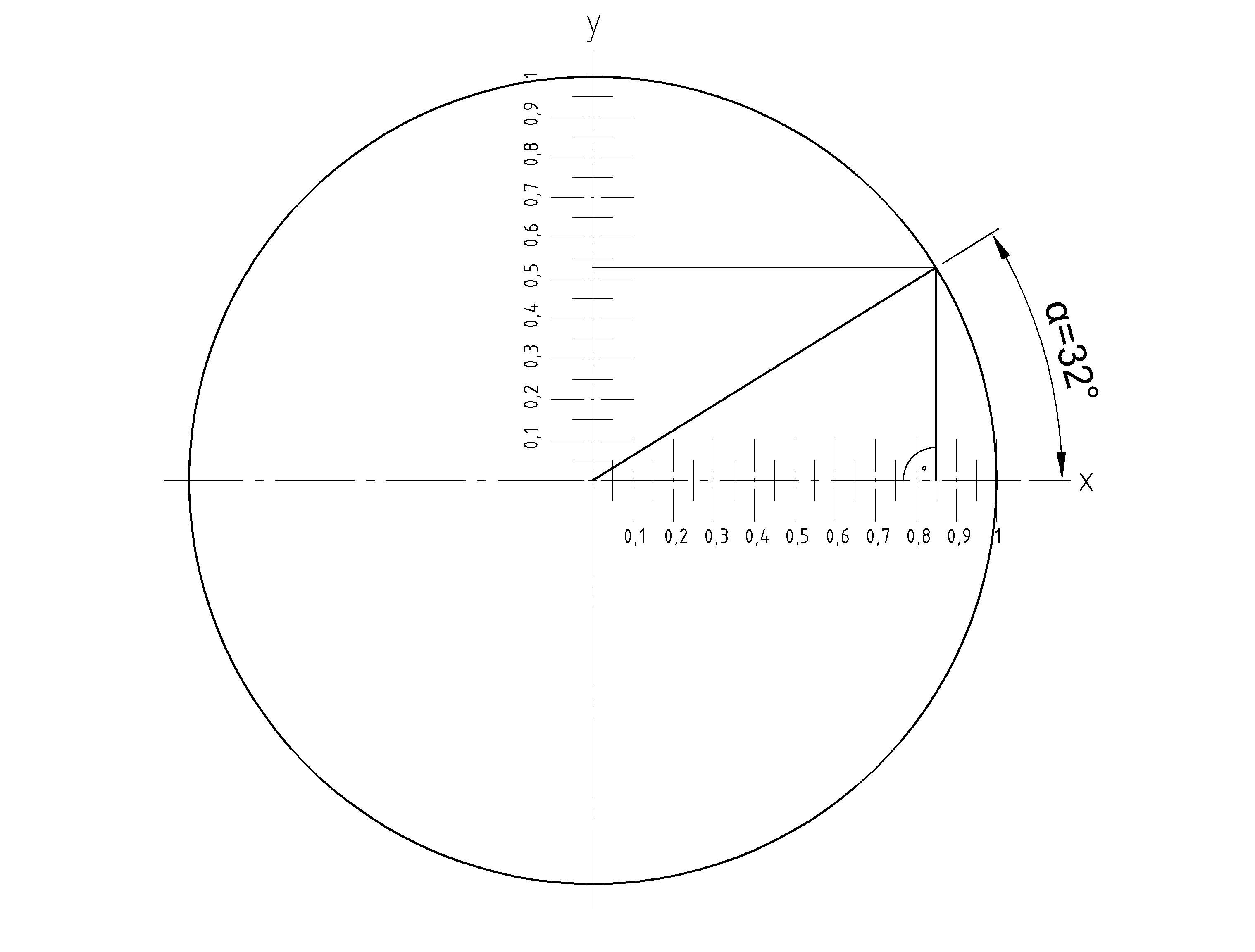
In diesem Kreis haben wir einen Winkel von 32° nun wissen wir das der Cosinus von 32° = 0,85 ist und der Sinus von 32° = 0,53. Wenn anders herum ein Cosinus oder ein Sinus Wert bekannt wären können wir unser Dreieck genauso gut zeichnen und den Winkel messen.

Radiant / Bogenmaß – Grad

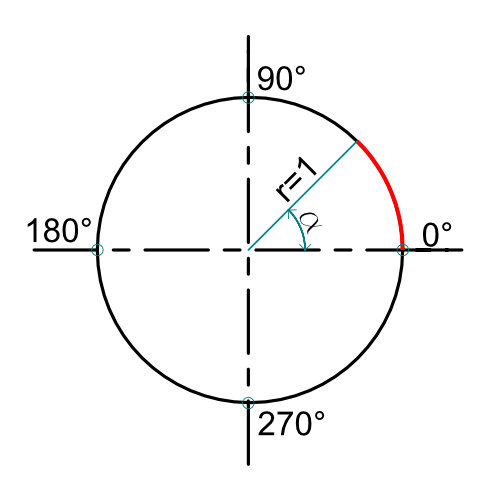
Der Einheitskreis kann auch dazu genutzt werden um das Verhältnis zwischen Radiant (Bogenmaß) und dem Winkel in Grad zu verdeutlichen. Nehmen wir uns also wieder einen Kreis der einen Radius von 1 hat. Dieses mal interessieren uns die X und Y Koordinaten jedoch nicht. Sondern das Bogenmaß also der Bogen, der am Kreisumfang entsteht, wenn wir eine Linie unter einem beliebigen Winkel auf den Kreis treffen lassen.

Die Formel für den Kreisumfang kennen sicher die meisten.

$U=\pi ·d = U=\pi ·r·2$

Benutzen wir jetzt unseren Einheitskreis um zu verdeutlichen wie sich das Verhältnis von Radiant zu Grad verhält setzen wir also den Wert 1 für den Radius ein.

$U=\mathrm{\pi }·1·2$

Da es keinen Unterschied macht ob die 1 in der Formel steht oder nicht (Das Ergebnis ist das selbe), kann man vereinfacht gesagt festhalten: Ein Kreis hat einen Umfang von 2π. Wenn wir unseren Kreis also einmal umrunden, haben wir gedanklich eine Strecke von 2 mal π (0-360°)zurückgelegt. Umrunden wir ihn nur zur Hälfte eine Strecke von 1 mal π (0-180°) usw… Daraus lässt sich folgende Tabelle ableiten:

Bei 180° haben wir nur π stehen. Also eignet sich dieser Wert am besten um daraus Formeln abzuleiten.

Radiant

$b=\alpha ·\frac{\mathrm{\pi }}{180°}$

Winkel

$\alpha =b·\frac{180°}{\mathrm{\pi }}$

Doch wozu das Ganze? Der Radiant ist eine andere Schreibweise bzw. eine andere Einheit einen Winkel anzugeben. In einigen Programmen z.B. Excel wird diese Einheit statt Grad verwendet. Wenn wir mit Winkelfunktionen in Excel rechnen müssen wir die Einheiten vorher umrechnen. Außerdem kann man diese Formeln mit dem Radius erweitern um die Bogenlänge bzw. den Winkel aus einem Bogen zu ermitteln.

Bogenlänge

$l_B=\frac{\mathrm{\pi }·\mathrm{r}·\mathrm{\alpha }}{180}$

Winkel

$\alpha =\frac{l_B·180°}{\mathrm{\pi }·\mathrm{r}}$