Quadratische Gleichungen

Quadratische Gleichungen sind Gleichungen bei denen die Lösungsvariable quadratisch ist. Beziehungsweise in einer Zweierpotenz vorkommt. Mehr dazu im Beitrag Potenzen.

reinquadratische Gleichungen

Die einfachste Form einer quadratischen Gleichung ist die reinquadratische Gleichung. Bei diesen Gleichungen kommt die Variable (meistens x) in quadratischer Form vor. Alles andere sind Zahlen. Bei diesen Gleichungen können wir die Gleichung einfach durch umstellen und radizieren (Wurzel nehmen) lösen.

reinquadratische Gleichungen haben das Muster: x² + q = 0

Beispiel 1

$$\begin{gathered} x^2 – 16 = 0 |+16 \\ {x}^{2 }= 16 |\sqrt{} oder –\sqrt{} \\ \left|x\right| = 4 \\ \mathbb{L}=\{4;–4\} \end{gathered}$$

Bei Quadratischen Gleichungen gibt es meistens 2 Lösungen. Deswegen müssen wir sowohl einmal + √ und einmal – √ nehmen.

Beispiel 2

Ein ähnliches Beispiel. Dieses mal steht die Gleichung jedoch in anderer Form da.

$(13x + 5) (13x – 5) = 119$

Durch multiplizieren erhalten wir eine besser lesbare Gleichung.

$$\begin{gathered} (13x + 5) (13x – 5) = 119 |ausmultiplizieren \\ 169x^2 –25 = 119 |+25 \\ 169x^2 = 144 |÷169 \\ {x}^2 = 0,852 |\sqrt{ } oder –\sqrt{} \\ \left|x\right| = 0,923 \\ \mathbb{L}=\{0,923;–0,923\} \end{gathered}$$

Beispiel 3

Die tragende Fläche einer Passfederverbindung soll wegen der zulässigen Flächenpressung mindestens 225 mm² betragen. Aus konstruktiven Gründen wird für die tragende Länge der Passfeder das 9fache der Wellen-Nuttiefe vorgeschlagen. Welche Wellen-Nuttiefe ist vorzusehen?

Lösung

Die tragende Fläche einer Passfeder ist ein Rechteck. Die angerundeten Bereiche einer Passfeder haben keinen Kontakt zur Mitnahmefläche. Wir erhalten also ein Rechteck mit einer gegebenen Fläche von 225 mm² und wir wissen, dass die Länge 9 mal länger ist als die Höhe. Wir wissen ebenfalls, dass die Formel zur Errechnung einer rechteckigen Fläche Länge · Höhe = Fläche ist.

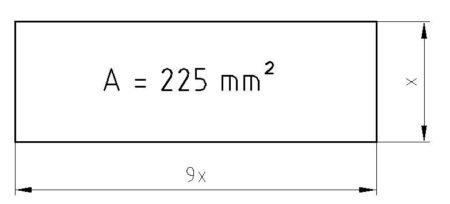
In einer Gleichung ausgedrückt heißt das:

$9x · x = 225$

Wir multiplizieren hier x mit x. Dies ist eine Zweierpotenz. Wir können also zusammenfassen.

$$\begin{gathered} 9x^2 = 225 |÷9 \\ x² = 25 |\sqrt{} \\ \left|x\right|=5 \\ \mathbb{L}=\{5;–5\} \end{gathered}$$

Die Wellennuttiefe x beträgt 5 mm.

Beispiel 4

Sieht auf den ersten Blick wüst aus. Ist aber genauso einfach. Erst einmal die Gleichung in eine besser lesbare Form bringen, indem die Brüche aufgelöst werden.

$$\begin{gathered} \frac{1}{5}{x}^2 – 0,0073 = \frac{\sqrt{3}}{2} |umformen \\ 0,2x^2 – 0,0073 = 0,866 |+0,0073 \\ 0,2x^2 = 0,8733 |÷0,2 \\ {x}^2 = 4,367 \\ \left|x\right| = 2,089 \\ \mathbb{L}=\{2,089;–2,089\} \end{gathered}$$

defektquadratische Gleichungen

defektquadratische Gleichungen sind gemischquadratische Gleichungen ohne Absolutglied. Diese haben das Muster x² + px = 0

Beispiel 5

$x^2 + 3x = 0$

Zunächst müssen wir ausklammern. Ausklammern können wir x da dies der größte gemeinsame Faktor ist. Dieser Vorgang wird auch faktorisieren genannt.

$$\begin{gathered} x^{2 }+ 3x = 0 |ausklammern \\ x (x + 3) = 0 \end{gathered}$$

Nun können wir den Rest mit Hilfe des Nullproduktes lösen. Dieses besagt, dass ein Produkt immer 0 ergibt, wenn einer der Faktoren 0 ist. Wir setzen also sowohl den Wert vor der Klammer 0 als auch das Ergebnis in der Klammer.

$$\begin{gathered} x_1 (x_2 + 3) = 0 \\ 0 (–3 + 3) = 0 \\ \mathbb{L}=\{0;–3\} \end{gathered}$$

gemischtquadratische Gleichungen

pq-Formel

Für das nächste Beispiel brauchen wir die pq-Formel. Die pq-Formel kann benutzt werden um quadratische Formeln zu lösen, die in der „Normalform“ vorliegen. Die pq-Formel sieht wie folgt aus.

$x_{1/2}=–\frac{p}{2}\pm \sqrt{{\left(\frac{p}{2}\right)}^2–q}$

• Das x ist unser gesuchter Wert. Oder besser gesagt ggf. unsere gesuchten Werte. Denn wir können x₁ und x₂ erhalten. Deswegen steht hinter dem x auch _1/2.
• p und q sind sogenannte Koeffizienten. Diese sind sozusagen Platzhalter für das was wir dort einsetzen.
• Das ± vor der Wurzel bedeutet, dass wir die Formel einmal mit + und einmal mit – rechnen müssen.
• Alles was unter der Wurzel steht ist die sogenannte Diskriminante.

Diskriminante

Die Diskriminante gibt an wie viele reelle Lösungen existieren.

• Ist der Wert der Diskriminante Negativ also < 0 so hat die Gleichungen keine Lösungen. Wir können also aufhören zu rechnen. Ggf. Begründungssatz.
• Ist der Wert der Diskriminante Genau 0 so hat die Gleichung eine Lösung nämlich – p/2 Denn eine Zahl mit 0 zu addieren oder zu subtrahieren ändert ihren Wert ja nicht. Deswegen kann die Wurzel ignoriert werden.
• Ist der Wert der Diskriminante Positiv also > 0 so hat die Gleichungen zwei mögliche Lösungen. Denn -p/2 plus das was unter der Wurzel steht oder minus das was unter der Wurzel steht ergeben zwei unterschiedliche Werte.

Normalform

Wie bereits erwähnt können wir die pq-Formel nur anwenden, wenn die Gleichung in Normalform vorliegt. Diese sieht wie folgt aus:

$x^2 + px + q = 0$

p und q sind Platzhalter die für irgendeine Variable stehen können. Vor dem x² darf nichts stehen! Ist dies der Fall müssen wir durch den davor stehenden Wert teilen um x² alleine stehen zu haben.

$$\begin{gathered} a{x}^2 + px + q = 0 |÷a \\ {x}^2 + \left(\frac{p}{a}\right)·x + \left(\frac{q}{a}\right) = 0 \\ \Downarrow \Downarrow \\ {x}^2 + p · x + q = 0 \end{gathered}$$

Der Wert vor dem x² darf auch nicht 0 sein! Denn wir wissen ja. Eine Division durch 0 ist in der Mathematik nicht erlaubt. a ≠ 0. Jetzt wissen wir, wie wir mit der pq Formel umgehen. Sehen wir uns das nächste Beispiel an.

Beispiel 6

Ein rechteckiges Blech mit einer Fläche von 6 cm² soll mit Hilfe eines Schneidwerkzeuges ausgeschnitten werden. Aufgrund einer begrenzten Schittkraft des Werkzeuges soll die Schnittkante rundherum maximal 10 cm betragen. Welche Abmessungen muss das Schneidewerkzeug haben?

Lösung

Wie in Beispiel 1 haben wir eine rechteckige Fläche. Dieses mal beträgt diese 6 cm². Außerdem kennen wir den Umfang, der 10 cm  ist. Die Formel Berechnung einer rechteckigen Fläche lautet Länge · Höhe = Fläche. Der Umfang kommt darin nicht vor. Der Umfang ist aber 2 · Länge + 2 · Höhe Das können wir also stattdessen umsetzen. Nennen wir die Höhe x und die Länge y.

$2·x + 2·y = 10 \left(Umfang\right)$

Was bringt uns das jetzt? Erst einmal nichts. Wir müssen zu einer Variable umstellen.

$$\begin{gathered} 2x + 2y = 10 |–2x \\ 2y = 10 –2x |÷2 \\ \underline{y = 5 – x} \end{gathered}$$

Soweit so gut. Jetzt können wir dies in unsere Flächenformel einsetzen (grün).

$$\begin{gathered} Fläche = Höhe · Länge \\ 6 = x · (5–x) |ausmultiplizieren \\ 6 = 5x – x^2 \end{gathered}$$

Damit wir die Gleich mit der pq-Formel lösen können, müssen wir sie erst einmal in die Normalform bringen. Bei der Normalform steht auf einer Seite 0. Das ist bei unserer Gleichung noch nicht der Fall. Dies müssen wir ändern.

$$\begin{gathered} 6 = 5x – x^2 |–6 \\ 0 = 5x –x^2 – 6 |umformen \\ 0 = –x^2 + 5x – 6 |·(–1) \\ 0 = x^2 – 5x + 6 \end{gathered}$$

Das umformen habe ich gemacht, damit man besser erkennen kann, was noch zu tun ist um die Gleichung in die Normalform zu bekommen. Nun können wir die Terme mit p und q ersetzen.

$$\begin{gathered} 0 = x^2 – 5x + 6 \\ \Downarrow \Downarrow \\ p q \end{gathered}$$

Dies setzen wir nun wiederum in unsere pq-Formel ein.

$$\begin{gathered} x_{1/2} = \frac{p}{2} \pm \sqrt{{\left(\frac{p}{2}\right)}^2 – q} \\ {x}_{1/2} = \frac{5}{2} \pm \sqrt{{\left(\frac{5}{2}\right)}^2 – 6} \\ {x}_{1/2} = 2,5 \pm \sqrt{{\left(2,5\right)}^2 – 6} \\ {x}_{1/2} = 2,5 \pm \sqrt{0,25} \\ {x}_{1/2} = 2,5 \pm 0,5 \\ \underline{x_1 = 3 \vee x_2 = 2} \end{gathered}$$

Beispiel 7

Ein Besipiel mit einem Wert vor dem x²

$$\begin{gathered} 0,8x^2 – 4,5x + 2 = 0 |÷0,8 \\ {x}^2 – \frac{4,5}{0,8}·x + \frac{2}{0,8} = 0 \\ {x}^2 – 5,625 · x + 2,5 = 0 \\ {x}^2 – p · x + q =0 \\ {x}_{1/2} = –\frac{–5,625}{2} \pm \sqrt{{\left(\frac{–5,625}{2}\right)}^2 – 2,5} \\ {x}_{1/2 }= 2,8125 \pm \sqrt{7,91 – 2,5} \\ {x}_{1/2} = 2,8125 \pm 2,326 \\ \mathbb{L}=\{5,1385;0,4865\} \end{gathered}$$

Beispiel 8

Ein Werkstück wird durch eine Kraft F = 4 kN belastet. Durch die Verlagerung und Erhöhung der Kraft um 0,5 kN wird die Kraftkomponente F1 um 0,3 kN kleiner und die Kraftkomponente F2 um 0,8 kN größer. Wie groß waren die Kräfte F1 und F2 vor der Verlagerung und Erhöhung?

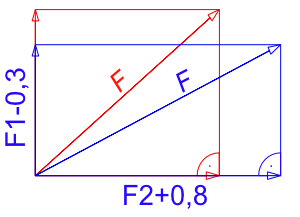
Zunächst haben wir zwei unbekannte und stellen dafür zwei Gleichungen auf. Gegeben sind jeweils ein X-Wert, ein Y-Wert und die Resultierende draus. Gemäß der Skizze erkennen wir, dass es sich dabei um rechtwinklige Dreiecke handelt und können daher den Satz des Pythagoras anwenden.

$$\begin{gathered} \mathrm{I} {{\mathrm{F}}_1}^2 + {{\mathrm{F}}_2}^2 = 4^2 \\ \mathrm{II} (\mathrm{F}1 – 0,3{)}^2 + ({\mathrm{F}}_2 + 0,8{)}^2 = 4,5^2 \end{gathered}$$

Anschließend stellen wir die Gleichung I nach F₂ um. Wir könnten auch nach F₁ umstellen.

$$\begin{gathered} {F_1}^2 + {F_2}^2 = 4^2 |–{F_1}^2 \\ {F_2}^2 = 4^2 – {F_1}^2 |\sqrt{} \\ {F}_2 = \sqrt{4^2 – {F_1}^2} \end{gathered}$$

Dann können wir die Gleichung I in die Gleichung II einsetzen. Wir tauschen also F₂ durch die umgestellte Gleichung aus.

_{$$\begin{gathered} {\left(F_1 – 0,3\right)}^2 + {\left(\sqrt{4^2–F_1} + 0,8\right)}^2 = 4,5^2 |2. bin. F. \& 1. bin. F. \\ {F_1}^2 – 2·F_1·\left(–0,3\right) + {\left(–0,3\right)}^2 + {\left(\sqrt{4^2–{F_1}^2}\right)}^{2*} + 2·\sqrt{4^2 – {F_1}^2}·0,8 + 0,8^2 = 4,5^2 \\ zusammenfassen \\ *Potenz und Wurzel heben sich auf. \\ \cancel{{F_1}^2} – 0,6F_1 + \underline{0,09} + \underline{16} \cancel{– {F_1}^2} + 1,6\sqrt{16–{F_1}^2} + \underline{0,64} = 20,25 \\ weiter zusammenfassen \\ –0,6F_1 + 16,73 + 1,6\sqrt{16 – {F_1}^2} = 20,25 |+0,6F_1 –16,73 \\ 1,6\sqrt{16–{F_1}^2} = 20,25 + 0,6F_1 – 16,73 |zusammenfassen \\ 1,6\sqrt{16–{F_1}^2} = 3,52 + 0,6F_1 |÷1,6 \\ \sqrt{16–{F_1}^2} = 2,2 + 0,375F_1 |quadrieren \\ 16 – {F_1}^2 = {\left(2,2 + 0,375F_1\right)}^2 |1. bin. F. \\ 16 – {F_1}^2 = 2,2^2 + 2 · 2,2 · 0,375F_1 + 0,375{F_1}^2 |zusammenfassen \\ 16 – {F_1}^2 = 4,84 + 1,65F_1 + 0,140625{F_1}^2 |–16 + {F_1}^2 \\ 0 = \underline{4,84} + 1,65F_1 + 0,140625{F_1}^2 \underline{– 16} + *{F_1}^2 |zusammenfassen \\ * wenn nichts vor der Variable steht ist diese 1 \\ 0 = –11,16 + 1,65F_1 + 1,140625{F_1}^2 |÷1,140625 \\ 0 = –9,78 + 1,45F_1 + {F_1}^2 |in Normalform umschreiben \\ 0 = {F_1}^2 + 1,45F_1 – 9,78 |pq–Formel \end{gathered}$$}

Jetzt können wir Die Gleichung anhand der pq-Formel lösen.

$$\begin{gathered} F_{1_{1/2}} =– \frac{1,45}{2} \pm \sqrt{{\left(\frac{1,45}{2}\right)}^2 – \left(–9,78\right)} \\ {F}_{1_1} =– \frac{1,45}{2} + \sqrt{{\left(\frac{1,45}{2}\right)}^2 – \left(–9,78\right)} \\ \underline{F_{1_1} = 2,49 kN} \\ {F}_{1_2} =– \frac{1,45}{2} – \sqrt{{\left(\frac{1,45}{2}\right)}^2 – \left(–9,78\right)} \\ \left[F_{1_2} = –3,94\right] \end{gathered}$$

Eine Minuskraft gibt es nicht, deshalb klammern wir den Wert ein. Nun können wir den gefundenen Wert in die Gleichung I einsetzen.

$$\begin{gathered} F_2 = \sqrt{16–2,{49}^2} \\ \underline{F_2 = 3,13 kN} \end{gathered}$$

Satz von Vieta

Der Satz von Vieta kann genutzt werden wenn eine quadratische Gleichung in Normalform (x² + px + q = 0) vorliegt. Der Satz von Vieta besagt:

$$\begin{gathered} x_1 + x_2 = –p \\ {x}_1 · x_2 = q \end{gathered}$$

Damit können wir z.B. Lösungen von quadratischen Gleichungen überprüfen.

Beispiel:

$$\begin{gathered} \mathbb{L}=\{4;–6\} \\ {x}_1 + x_2 = –p \\ 4 + (–6) = –2 |·(–1) \\ p = 2 \\ {x}_1 · x_2 = q \\ 4 · (–6) = –24 \\ q = –24 \\ {x}^{2 }+ 2x –24 = 0 \end{gathered}$$