Reihen- Parallelschaltung

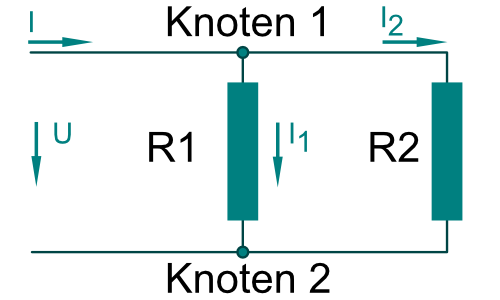
Kirchhoff’sche Gesetz 1 „Knotenregel“

Die Summe der auf einen Knoten zufließenden Ströme ist gleich der Summe der von ihm abfließenden Ströme.

$Σ I_{z u} = Σ I_{a b}$

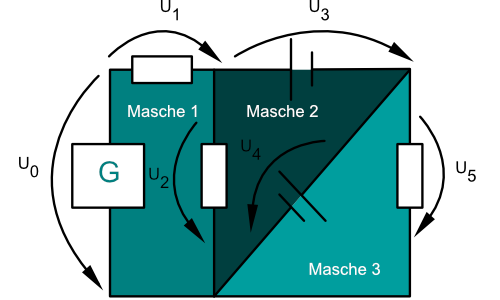
Kirchhoff’sche Gesetz 2 „Maschenregel“

Bei einel elektrischen Netzwerk ist die Summe der Spannungen in einer Masche null, wenn man von einem Knoten aus auf beliebigem Weg die Masche durchläuft.

$Σ U_{i} = 0 i = a l l e E l e m e n t e$

Aus deb Kirchhoff’schen Gesetzen können die Gesetze für Reihen- und Parallelschaltungen abgeleitet werden.

Parallelschaltung

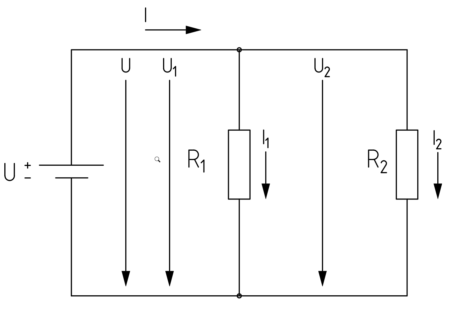
$I = I_{1} + I_{2} (K n o t e n r e g e l) \frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$

$U = U_{1} = U_{2} = U_{3}$

Reihenschaltung

Bei Reihenschaltungen ist die Summe aller Teilspannungen gleich der Gesamtspannung. An jedem Widerstand hat man einen Spannungsabfall.

$U = U_{1} + U_{2} + U_{3} (M a s c h e n r e g e l)$

$I = I_{1} = I_{2} = I_{3}$

$R = R_{1} + R_{2} + R_{3}$

Beispiel

Eine kombinierte Reihen- Parallelschaltung

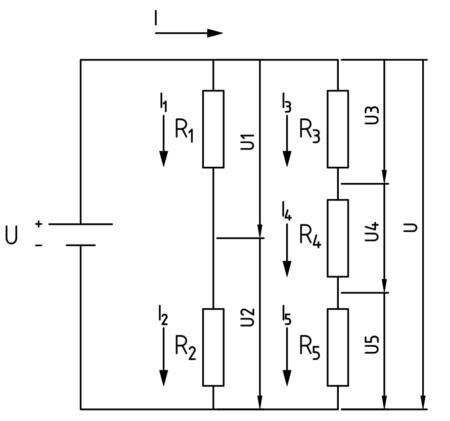
Gegeben:
U = 60 V
I₂ = 0,75 A
R1 = 20 Ω
R3 = 40 Ω
R4 = 80 Ω
R5 = 120 Ω

Wir wissen, dass in einer Reihenschaltung die Teilströme alle gleich sind. Also ist I₁=I₂ damit können wir U₁ ausrechnen.

$U_{1} = R_{1} \cdot I_{1} U_{1} = 20 Ω \cdot 0, 75 A U_{1} = 15 V$

Wir wissen auch, dass die Summe der Teilspannungen in einer Reihenschaltung die Gesamtspannung ergibt. Da wir diese gegeben haben und eine Teilspannung kennen, können wir durch Subtrahieren die Differenz ermitteln.

$U_{2} = U - U_{1} U_{2} = 60 V - 15 V U_{2} = 45 V$

Die Spannung ist in der zweiten Reihe mit drei Widerständen die selbe wie in der ersten Reihe. Das besagt die Regel für Parallelschaltungen.

Der Gesamtwiderstand einer Reihe ist die Summe der Einzelwiderstände.

$I_{3} = \frac{U}{R_{1} + R_{2} + R_{3}} I_{3} = \frac{60 V}{40 Ω + 80 Ω + 120 Ω} I_{3} = I_{4} = I_{5} = 0, 25 A$

Nun haben wir alle Teilströme und alle Widerstände und können die Spannungen berechnen.

$U_{3} = R_{3} \cdot I_{3} U_{3} = 40 Ω \cdot 0, 25 A U_{3} = 10 V U_{4} = R_{4} \cdot I_{4} U_{4} = 80 Ω \cdot 0, 25 A U_{4} = 20 V U_{5} = R_{5} \cdot I_{5} U_{5} = 120 Ω \cdot 0, 25 A U_{5} = 30 V$

$U = U_{3} + U_{4} + U_{5} U = 60 V$

Nun da wir die Teilspannungen und alle Teilströme kennen, können wir auch den Widerstand R₂ berechnen.

$R_{2} = \frac{U_{2}}{I_{2}} R_{2} = \frac{45 V}{0, 75 A} R_{2} = 60 Ω$

Anschließend ermitteln wir den Gesamtstrom I. Dieser ist die Summe aus beiden Reihen.

$I = I_{R 1} + I_{R 2} I = 0, 75 A + 0, 25 A I = 1 A$

Nun können wir den Gesamtwiderstand ermitteln.

$R = \frac{U}{I} R = \frac{60 V}{1 A} R = 60 Ω$

Wie die elektrische Leistung ermittelt wird, habe ich in dem Beitrag Grundlagen der Elektrotechnik erklärt.

$P = U \cdot I P = 60 V \cdot 1 A P = 60 V \cdot A \Rightarrow 60 W$

Schreibe einen Kommentar