Kondensatoren

Kondensatoren sind zwei ungleichartig elektrisch geladene Körper, welche einen bestimmten Abstand zueinander haben. Kondensatoren können elektrische Energie in Form eines elektrischen Feldes für eine gewisse Zeit speichern. Kapazität und die Höhe der Spannung sind entscheidend dafür wie viel Energie gespeichert werden kann.

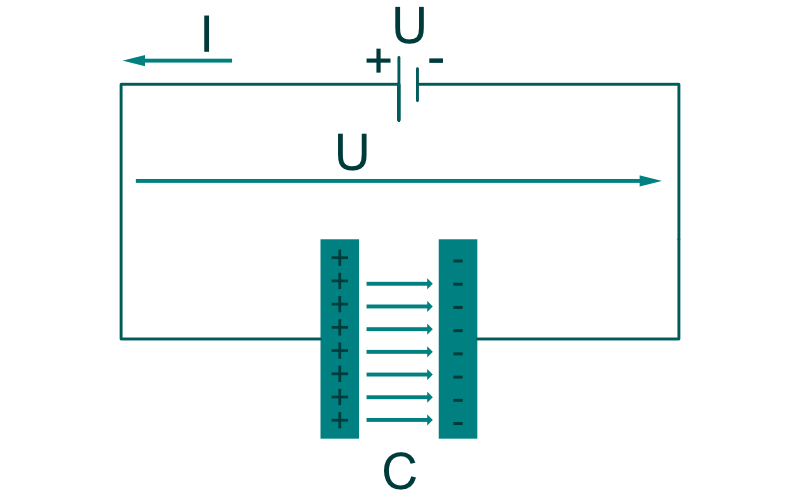
Schauen wir uns das am Schaltplan an. Das mit C gekennzeichnete Bauteil ist der Kondensator. Sobald wir den Schalter schließen kann Strom fließen. Der Pluspol zieht die Elektronen an. Da zwischen den Kondensatorteilen aber ein schlechter Elektrischer Leiter eingesetzt wird, können die Elektronen hier nicht weiter.

Eine Seite des Kondensators ist also positiv, die andere negativ geladen. Zwischen diesen Teilen entsteht ein elektrisches Feld, da die Elektronen die Protonen anziehen. Die Ladungen erfahren dabei eine Kraft. Diese wird elektrische Feldkraft genannt.

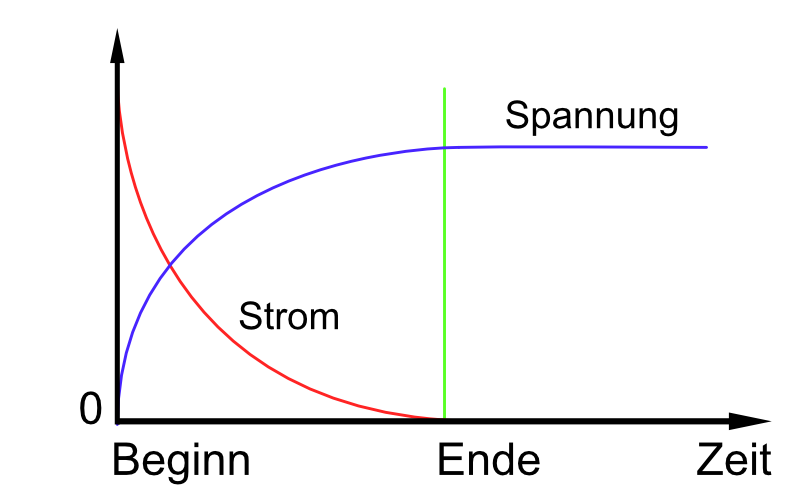
Strom und Spannung verlaufen genau entgegengesetzt zueinander. Das geschieht entgegengesetzt zur Spule. Der Strom eilt vor.

Formelzeichen

Formeln

Kapazität

$C={\epsilon }_0· {\epsilon }_r · \frac{(n–1) · A}{d}$

elektrische Energie

$W_{\mathrm{el}}=\frac{1}{2}·C·U²$

Ladungsmenge

Elektrische Ladung entsteht immer dann wenn ein Überschuss oder ein Mangel, ruhender elektrischer Ladungsträger vorliegt.

$Q=C·U$

Kondensatoren in Reihe geschaltet

$\frac{1}{C_{\mathrm{ges}}}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3} \dots$

Kapazität Kondensatoren parallel geschaltet

$C_{\mathrm{ges}}=C_1+C_2+C_3 \dots$

Dielektrikum / Dielektrizitätszahl ε_r

Die Dielektrizitätszahl ε_r dient als Maß für die Isolierstärke eines Werkstoffes im Bezug auf die Kapazität eines Kondensators. Je höher die Zahl, desto mehr Kapazität kann bei gleicher Bauform erreicht werden.

Beispielwerte

Beispiel 1

Die Platten eines Plattenkondensators haben eine Fläche von 12 cm². Dazwischen liegt eine 0,5 mm dicke Quarzglasplatte.

Kapazität

$$\begin{gathered} C=8,8542 \frac{pF}{\cancel{m}}·4,2 · \frac{0,012 \cancel{m}²}{0,005 \cancel{m}} \\ C=89,25 pF \end{gathered}$$

Wie viel Platten werden benötigt, wenn die Plattenfläche auf 3 cm² verkleinert wird?

Dazu stellen wir die Formel nach n um und tragen dann dort unsere Werte ein.

$$\begin{gathered} C={\epsilon }_0·{\epsilon }_r\frac{(n–1)·A}{d} |·d \\ C·d={\epsilon }_0·{\epsilon }_r·(n–1)·A |÷({\epsilon }_0·{\epsilon }_r·A) \\ \frac{C·d}{{\epsilon }_0·{\epsilon }_r·A}=n–1 |+1 \\ \frac{C·d}{{\epsilon }_0·{\epsilon }_r·A}+1=n \\ n=\frac{C·d}{{\epsilon }_0·{\epsilon }_r·A}+1 \\ n=\frac{89,25 pF ·0,5 · m}{8,8542 pF ·4,2 ·3 m² ·{10}^4}+1 \\ n=5 \end{gathered}$$

Beispiel 2

Es ist die Kapazität eines Kondensators zu ermitteln, der 3,6 sek lang mit einer Stromstärke von 10 mA auf 80 V aufgeladen wurde.

Beispiel 3

In einer Reihe sind zwei Kondensatoren mit Kapazitäten von einmal 3 µF und 6,8 µF geschaltet. Die Gesamtspannung beträgt 48 V.

Zu ermitteln:

1. Gesamtkapazität
2. Gesamtladung
3. Teilspannungen

1.

$$\begin{gathered} \frac{1}{C_{\mathrm{ges}}}=\frac{1}{C_1}=\frac{1}{C_2} \\ \frac{1}{C_{\mathrm{ges}}}=\frac{1}{3 \mu F}=\frac{1}{6,8 \mu F} \\ {C}_{ges}=2,08 \mu F \end{gathered}$$

2.

$$\begin{gathered} Q=C · U \\ Q=\frac{0,00208 As}{\cancel{V}} · 48 \cancel{V} \\ Q = 0,1 As \end{gathered}$$

$$\begin{gathered} Q=I · t \\ Q=0,010 A · 3,6 s \\ Q=0,36 As \end{gathered}$$

$$\begin{gathered} Q=C · U |÷U \\ \frac{Q}{U}=C \\ C=\frac{0,36 As}{80 V} \\ C=0,0045 As/V \Rightarrow 0,00 45 F \end{gathered}$$