Freimachen | Freischneiden

Der Sinn und Zweck des freischneidens/Freimachens ist alle am Bauteil angreifenden Kräfte zu erfassen. Dabei werden alle angrenzenden Bauteile auf ihre Kräfte reduziert, die sie auf das freizumachende Bauteil ausüben.

Beispiel

Unter realistischen Bedingungen sicher selten zu finden, soll uns aber für das Prinzip egal sein. Ein Motor hängt an Seilen in einem Stahlbau.

Beim Freimachen wird das Bauteil nun von allen angrenzenden Bauteilen getrennt. Zunächst wird das Bauteile ohne angrenzende Bauteile in seinen groben Konturen skizziert. Dann werden die Angriffspunkte (Kreise) der angreifenden Kräfte sowie deren Wirklinien festgelegt. Anschließend wird der Richtungssinn (Pfeilrichtung) auf das Freigemachte Bauteil übertragen. Begonnen wird mit den einfachsten Bauteilen. In diesem Beispiel also die Seile, da diese nur Zugkräfte übertragen können.

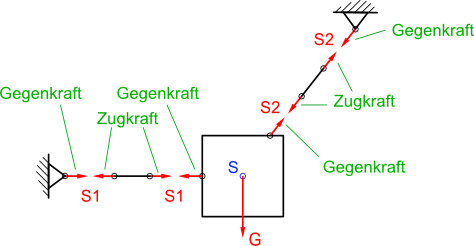
Um ein Kräftegleichgewicht zu schaffen hat jede Kraft eine gleich große Gegenkraft. So haben die Zugkräfte S₁ und S₂ auf ihrer Wirklinie jeweils eine gleich große Gegenkraft. Dieser Umstand wird auch als Aktionskraft und Reaktionskraft bezeichnet.

Weitere Beispiele

Seile, Ketten, Riemen

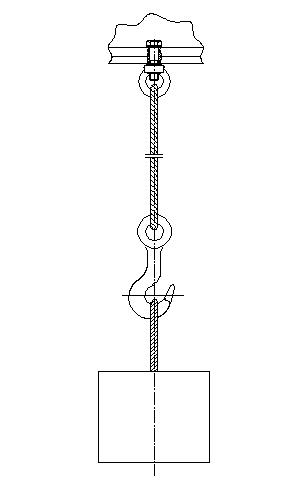
Seile, Ketten, Riemen oder ähnlich flexible Bauteile können nur Zugkräfte übertragen. Dies bedeutet, dass die Pfeilrichtung immer von diesen Bauteilen weg zeigt.

$S_1=F_G$

Zweigelenkstäbe (Pendelstütze)

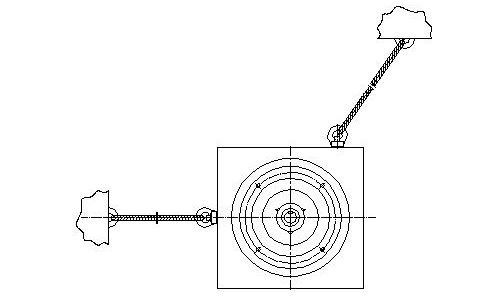
Zweigelenkstäbe oder auch Pendelstützen genannt können nur Zug oder Druckkräfte aufnehmen, deren Wirkrichtung die Verbindungsgerade der Gelenkpunkte ist. Die Gelenke werden als reibungsfrei angesehen.

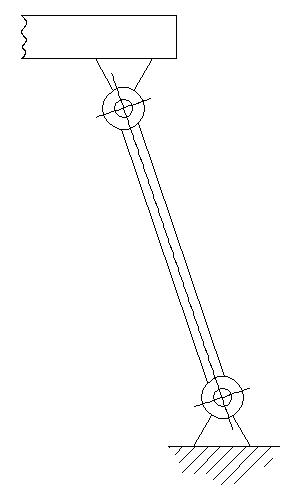
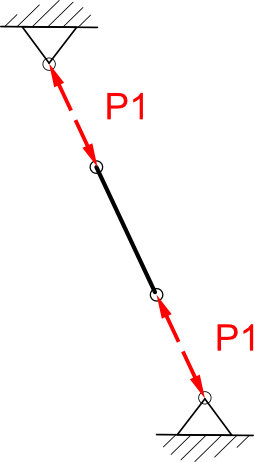
Die Pendelstütze kann Zug oder Druckkräfte aufnehmen um die obere Plattform daran zu hindern zu stark abzusinken oder abzuheben.

Berührungsflächen (ebene Stützflächen)

Berührungsflächen können Normalkräfte und Tangentialkräfte aufnehmen. Normelkräfte wirken immer in Richtung Berührungsfläche am freigemachten Bauteil.

Daraus folgt, dass immer eine Normalkraft N  zwischen zwei Bauteilen wirkt, wenn sie sich berühren. Die Normalkraft steht dabei stets rechtwinklig zur Berührungsfläche.

Die Tangentialkraft T wird durch Reibung oder (Reibungskraft R) oder einen Rollwiderstand hervorgerufen. Die Wirklinie der Tangentialkraft steht dabei rechtwinklig zur Wirklinie der Normalkraft. Der Richtungssinn ergibt sich aus der Bewegung des Bauteils und wirkt dieser entgegen. Liegt z.B. eine Kiste auf einer schiefen Ebene so wirkt die Reibung der Rutschbewegung entgegen.

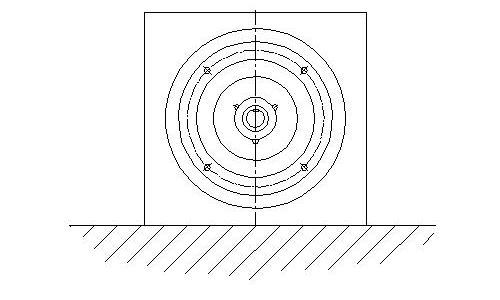
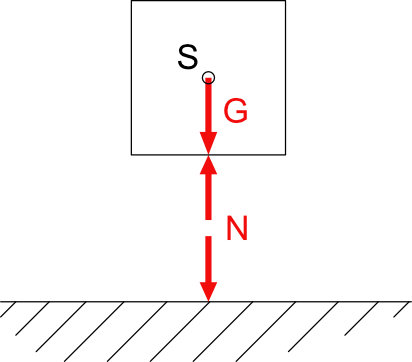
Die Gewichtskraft G und die Normalkraft N haben dieselbe Wirklinie WL und den gleichen Betrag und sind somit im Gleichgewicht.

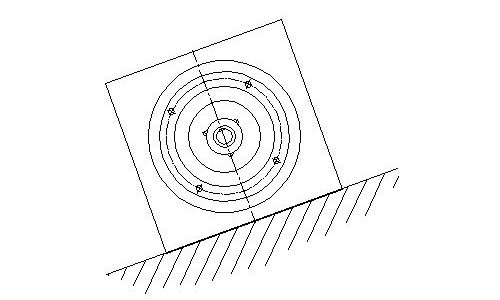
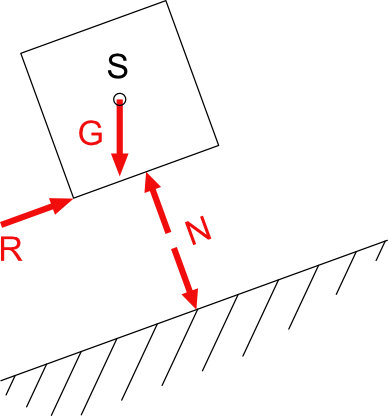
Hier können die Normalkraft N und die Gewichtskraft G nicht im Gleichgewicht sein. Der Körper würde die schiefe Ebene abwärts rutschen. Die Reibungskraft R verhindert dies und sorgt für das Gleichgewicht.

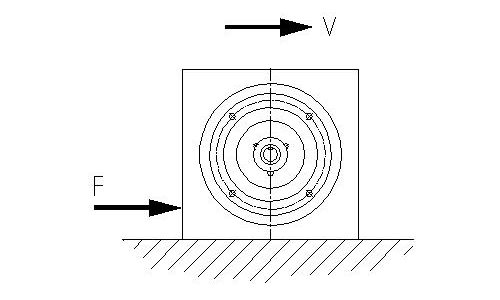
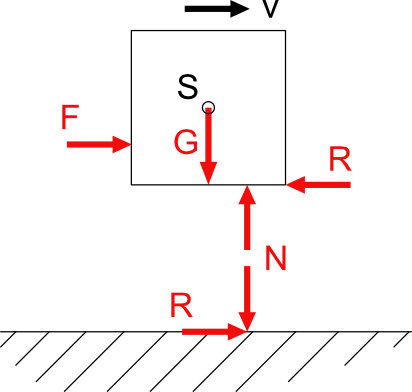
Hier bilden die Kraft F und die Reibungskraft R ein rechtsdrehendes Kräftepaar. Die Wirklinie WL von der Normalkraft N muss sich hier also verschieben um mit der Gewichtskraft G ein linksdrehendes Kräftepaar zu bilden, welches sich dem „entgegenstellt“. Ansonsten wäre hier kein Gleichgewicht gegeben.

Warum ist das so? Die Kraft F und die Reibungskraft R haben nicht die selbe Wirklinie WL, dadurch entsteht ein Wirkabstand l (Hebelarm) dieser erzeugt gemeinsam mit einer Kraft ein Kraftmoment M (Drehmoment). Damit alles wieder ins Gleichgewicht kommt, muss also die Wirklinie der Normalkraft N verschoben werden um ein Kraftmoment mit einem entgegengesetzten Drehsinn zu erzeugen. Daraus resultiert: ΣM=0

Rollkörper (gewölbte Stützflächen)

Rollkörper können Normalkräfte (Radialkräfte) und Tangentialkräfte aufnehmen. Die Normalkräfte wirken dabei immer auf den Berührungspunkt am freigemachten Körper.

Es kann sowohl die Bezeichnung Radialkraft als auch Normalkraft verwendet werden. Beide Wirklinien WL stehen stets rechtwinklig auf dem äußersten Berührungspunkt. Eine Tangentialkraft oder Reibungskraft tritt am ruhenden Rollkörper nur unter den selben Bedingungen auf wie an Berührungsflächen.

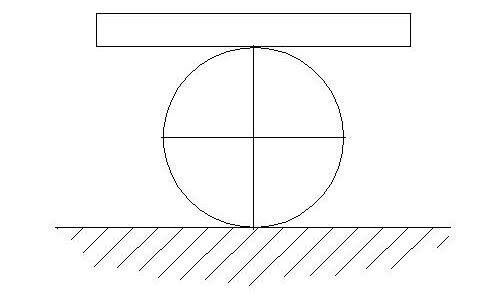
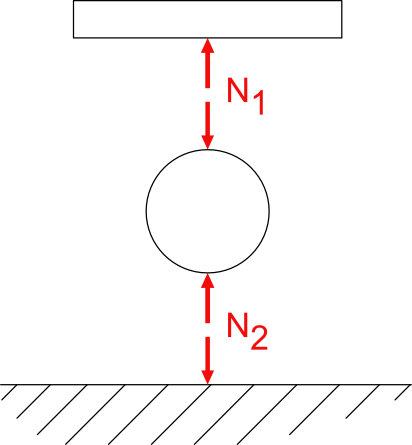
Die beiden Radialkräfte/Normalkräfte haben dieselbe Wirklinie und sind im Gleichgewicht.

Einwertige Lager (Loslager)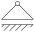  

Wirkweise

Sowohl Drehungen um den Lagerpunkt als auch eine Verschiebung in Richtung der Bewegungsbahn sind bei einwertigen Lagern möglich und werden nicht durch das Lager begrenzt. Einzig Bewegungen rechtwinklig zur Bewegungsbahn werden gesperrt. Loslager können daher nur Kräfte aufnehmen, deren Wirklinie WL rechtwinklig zur Stützfläche stehen, also nur Normalkräfte N.

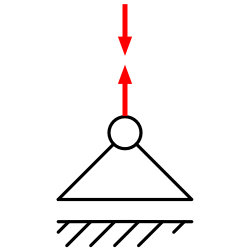
Einwertige Lager (Loslager) werden z.B. verwendet wenn ein Träger auf zwei Stützen aufliegt um Längenausdehnungen etc. zu kompensieren.

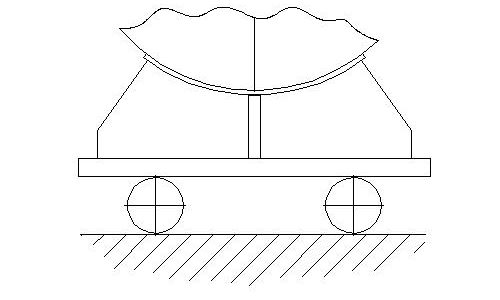
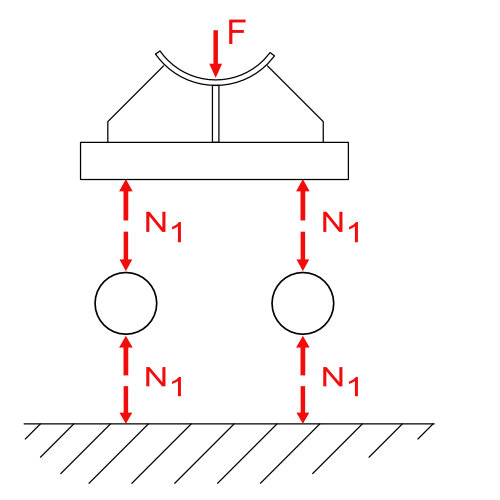
Wird ein einwertiges Lager in Längsrichtung verschoben, so bleibt das gelagerte Lager in Ruhe und verschiebt sich nicht mit. Das gelagerte Bauteil liegt lose auf dem Lager. Deswegen nennt man einwertige Lager auch Loslager.

Zweiwertiges Lager (Festlager)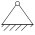 

Wirkweise

Zweiwertige Lager erlauben wie einwertige Lager eine Drehbarkeit am Lagerpunkt. Horizontale oder vertikale Verschiebungen werden blockiert. Ein Zweiwertiges Lager (Festlager) kann daher Kräfte in beliebiger Richtung aufnehmen. Beim Freimachen kennt man den tatsächlichen Richtungssinn oft noch nicht. Deshalb wird die unbekannte Lagerkraft durch zwei rechtwinklig zueinander wirkende Kräfte ersetzt. Diese werden mit dem Index für die jeweilige Achse bezeichnet. Haben wir unser Lager beispielsweise A genannt würden die Kräfte A_x und A_y heißen. Sowohl die tatsächliche Wirklinie WL als auch der Betrag der Kraft sind unbekannt.

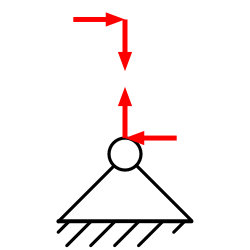
Träger auf zwei Stützen, Wellen und Achsen erhalten ein Zweiwertiges Lager (Festlager) an die Stelle an der eine Längsverschiebung verhindert werden soll. Zweiwertige Lager können anhand der Bewegungsprobe erkannt werden:

Wird das zweiwertige Lager in Längsrichtung verschoben, so wird auch das gelagerte Bauteil mit verschoben. Die beiden Elemente sind miteinander fest verbunden. Deswegen nennt man zweiwertige Lager auch Festlager

Beispiel: Rohrleitung

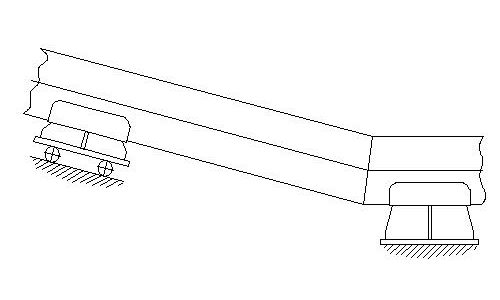
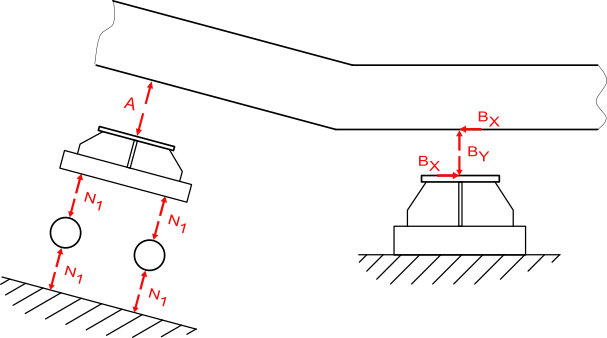
Das Loslager A ist ein einwertiges Lager und kann daher nur Normalkräfte übertragen. Das Festlager B ist zweiwertig. Die Wirklinie ist unbekannt, deshalb werden Kräfte in X und Y Achse angenommen. Auch der Richtungssinn kann nur angenommen werden. Das Ergebnis kann die Annahme entweder bestätigen oder wiederlegen.

Beispiel: Tür

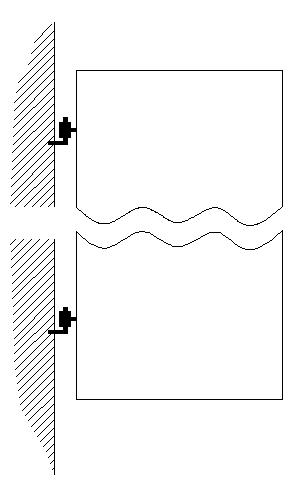
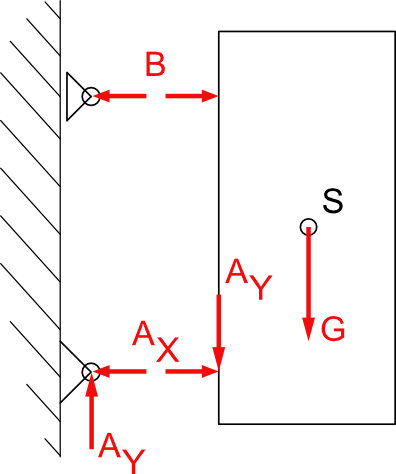
Das Lager B ist ein einwertiges Lager (Loslager). Hier wirkt nur die Normalkraft rechtwinklig auf das Bauteil. Das Lager A ist ein zweiwertiges Lager (Festlager) Auch hier nehmen wir wieder die Wirklinien in X und Y Achse an.

Beispiel: Welle

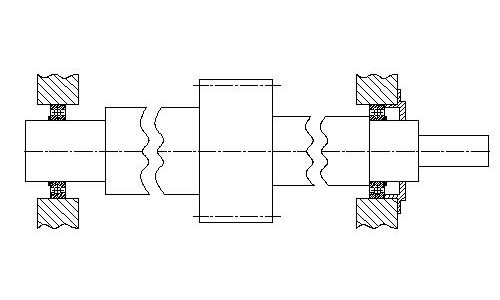
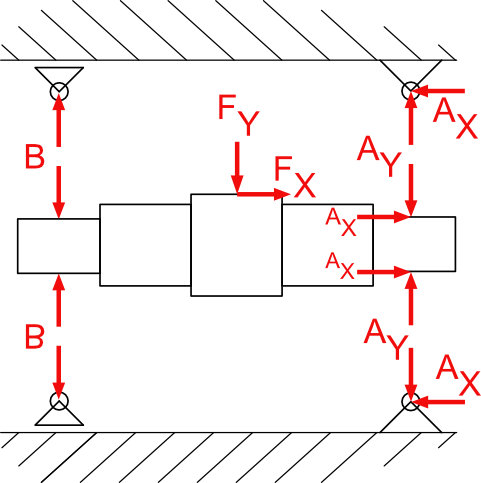
Durch ein Zahnrad werden die Kräfte F_X und F_y auf die Welle übertragen. Das Loslager B kann nur Normalkräfte aufnehmen. Die Kraft F_X in Längsrichtung kann also nur vom Festlager A aufgenommen werden. Daraus resultiert: F_X = A_X

Beispiel: Schwenkarm

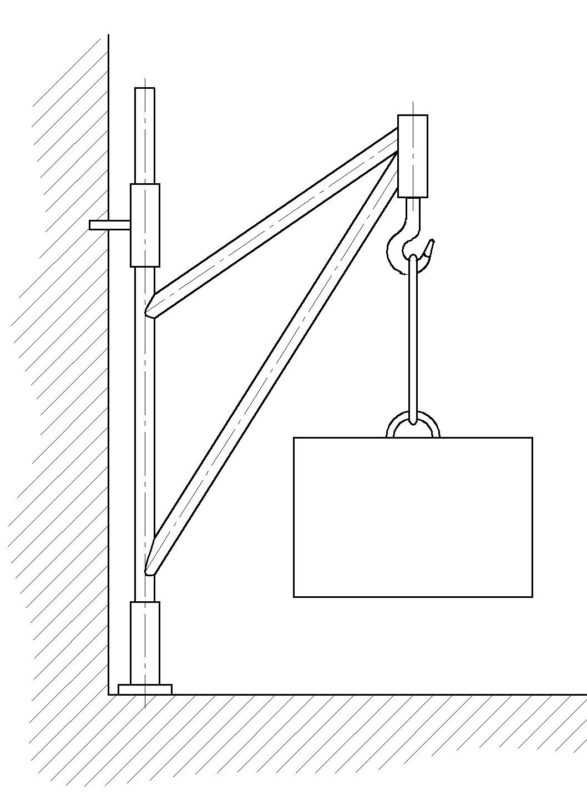
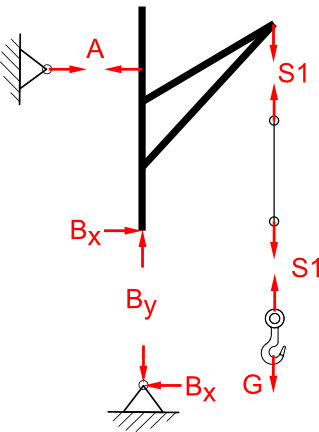
Die Bewegungsprobe ergibt, das Lager A kann in Y Richtung verschoben werden, ohne das sich das Bauteil bewegt, in X Richtung jedoch nicht. Drehen kann es sich auch. Also ist nur ein Freiheitsgrad eingeschränkt. Es handelt sich also um ein einwertiges Lager (Loslager).

Für das Lager B sieht die Sache schon ganz anders aus. Das Lager kann sich zwar drehen, jedoch weder in X noch in Y Achse bewegen, ohne das sich das Bauteil mit bewegt. Es sind also zwei Freiheitsgrade eingeschränkt. Also ist es ein zweiwertiges Lager (Festlager).

Der Richtungssinn für das zweiwertige Lager ergibt sich ebenfalls aus der Bewegungsprobe. Würde man das Lager B entfernen, würde sich das Bauteil aufgrund der Gewichtskraft im Uhrzeigersinn, also nach links um das Lager A drehen. Also muss die Kraft B_x am Bauteil von Links nach rechts wirken um dem entgegenzuwirken.

Dreiwertige Lager (z.B. Einspannung) 

Wirkweise

Bei dreiwertigen Lagern wird jede Bewegungsmöglichkeit gesperrt. (Verschiebung und Drehung). Dreiwertige Lager können daher Kräfte in beliebiger Richtung und ein Kraftmoment aufnehmen. Beim Freimachen ersetzt man wie beim Festlager die Lagerkraft durch zwei rechtwinklige Kräfte in X und Y Achse. Beim dreiwertigen Lager wird dann noch das Kraftmoment durch den Momentendrehpfeil ⤻  ⤺ ⤹ ⤸ ergänzt. Auch hier sind Wirklinie WL, Kraftbetrag sowie der Betrag des Kraftmoments unbekannt.

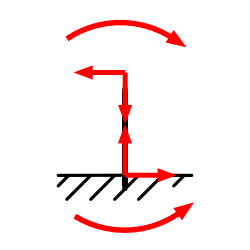
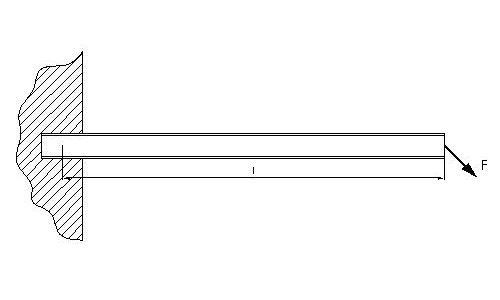
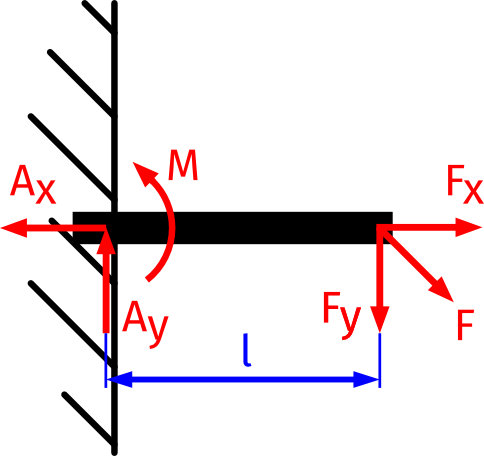
Der Träger ist in der Wand einbetoniert. Die Kraft F_y ist also gleich A_y sowie die Kraft F_x = A_x. Das Kraftmoment M hat den Betrag von F_y · l