Variablen
Logische Verknüpfungen verknüpfen Abfragen zu den Wahrheitswerten WAHR oder FALSCH. In der Digitaltechnik kann eine Variable nur die Werte 0 oder 1 haben.
- 0 = FALSCH (Bedingung nicht erfüllt)
- 1 = WAHR (Bedingung erfüllt)
Algebraische Formelsymbole
| ∧ | Konjunktion: A UND B | WAHR wenn A UND B WAHR |
| ∨ | Disjunktion: A ODER B | WAHR wenn A ODER B WAHR |
| → | Implikation: WENN A DANN B | WAHR wenn aus A B folgt |
| ¬ | Negation: NICHT A | WAHR wenn A FALSCH ist oder umgekehrt |
| ↔ | Äquivalenz: GENAU B | WAHR wenn A UND B den selben Wahrheitswert haben |
| ⊕ | Antivalenz: A Exklusiv ODER B | WAHR wenn entweder A ODER B WAHR sind, aber nicht beides |
| ↑ | Shefferfunktion: NICHT (A UND B) | ∧ oder ∨ |
| ↓ | Peircfunktion: NICHT (A ODER B) | Weder A noch B |
Verknüpfungen
In der Digitaltechnik gibt es drei logische Grundverknüpfungen.
- NICHT
- UND
- ODER
Die Grundfunktionen können zu anderen Funktionen kombiniert werden. Es folgt eine Übersicht der gängigsten Funktionen.
Negation (NICHT-NOT) ¬
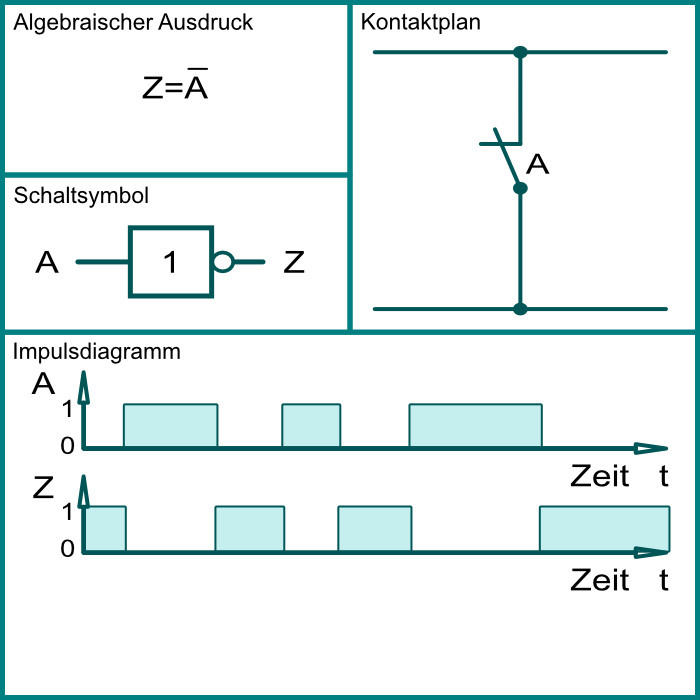
| Wahrheitstabelle | |
| A | Z |
| 0 | 1 |
| 1 | 0 |
Die Ausgabevariable ist WAHR wenn die Eingabevariable FALSCH ist.
Konjunktion (UND-AND) ∧
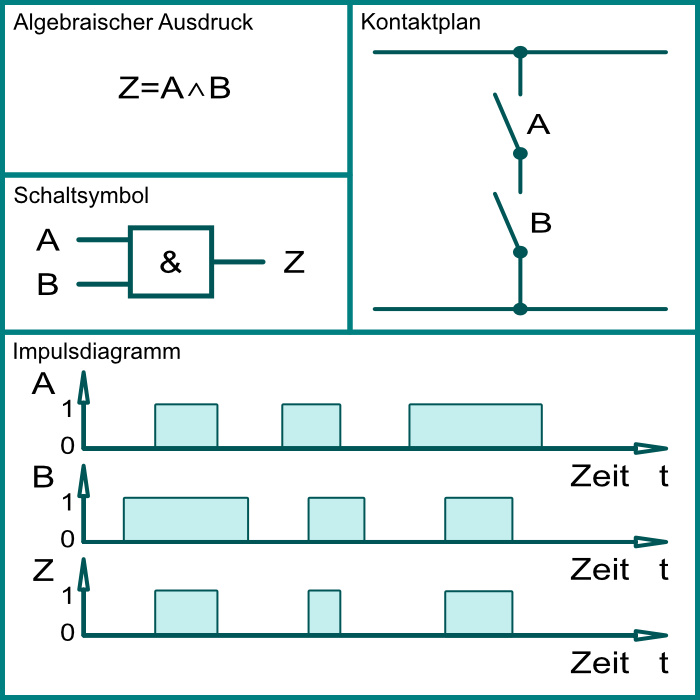
| Wahrheitstabelle | ||
| A | B | Z |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Die Ausgabevariable ist nur dann WAHR wenn alle Eingabevariablen WAHR sind.
Disjunktion (ODER-OR) ∨
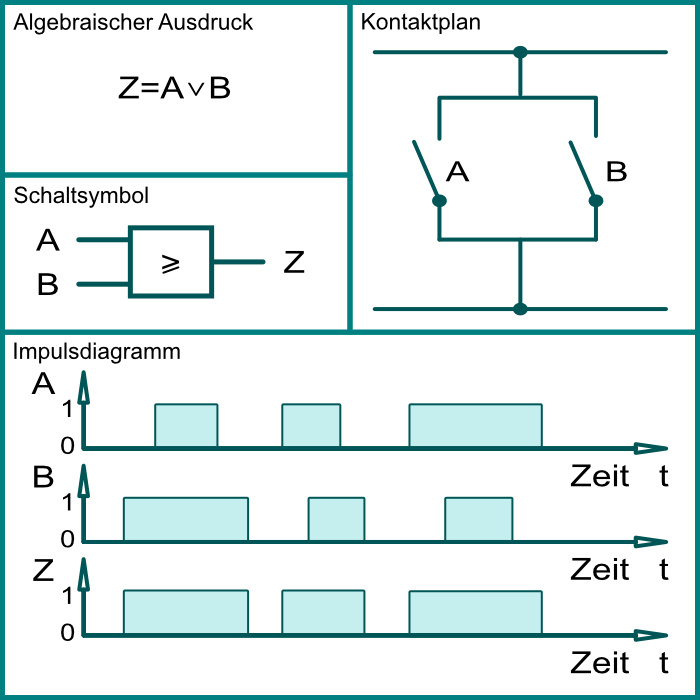
| Wahrheitstabelle | ||
| A | B | Z |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Die Ausgangsvariable ist dann WAHR wenn eine der Eingangsvariablen WAHR ist.
Antivalenz (Exklusiv ODER-XOR) ⊕
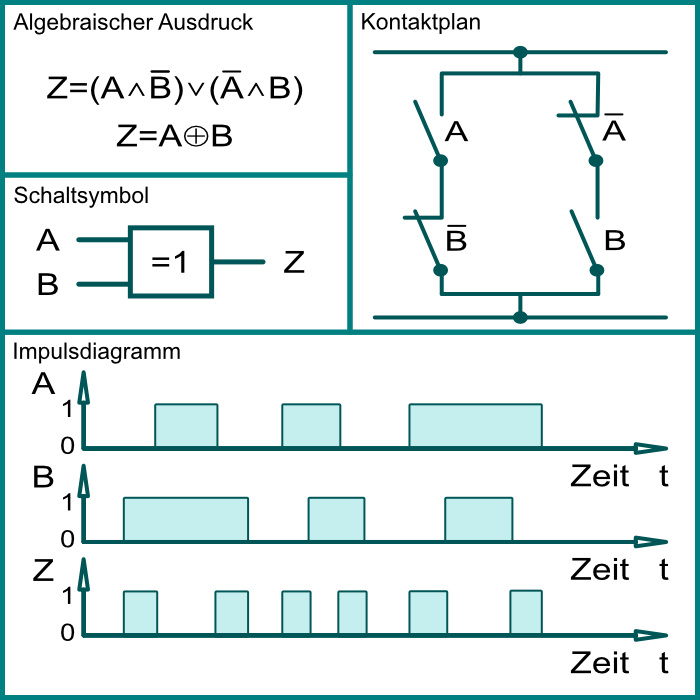
| Wahrheitstabelle | ||
| A | B | Z |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Die Ausgangsvariable ist WAHR wenn eine der Eingangsvariablen WAHR ist aber nicht beide.
Äquivalenz (Exklusiv NICHT ODER-EXNOR) =
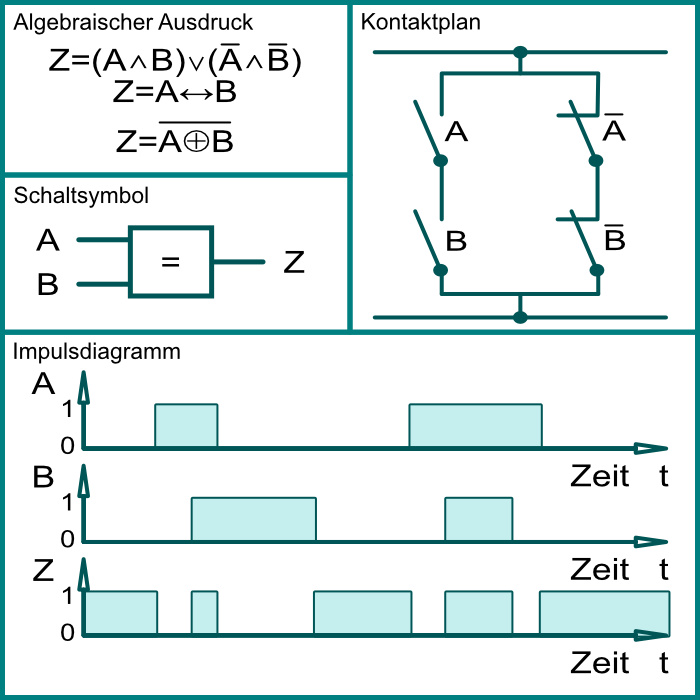
| Wahrheitstabelle | ||
| A | B | Z |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Die Ausgangsvariable ist WAHR wenn beide Eingangsvariablen denselben Wahrheitswert haben.
Schefferfunktion (NICHT UND-NAND)
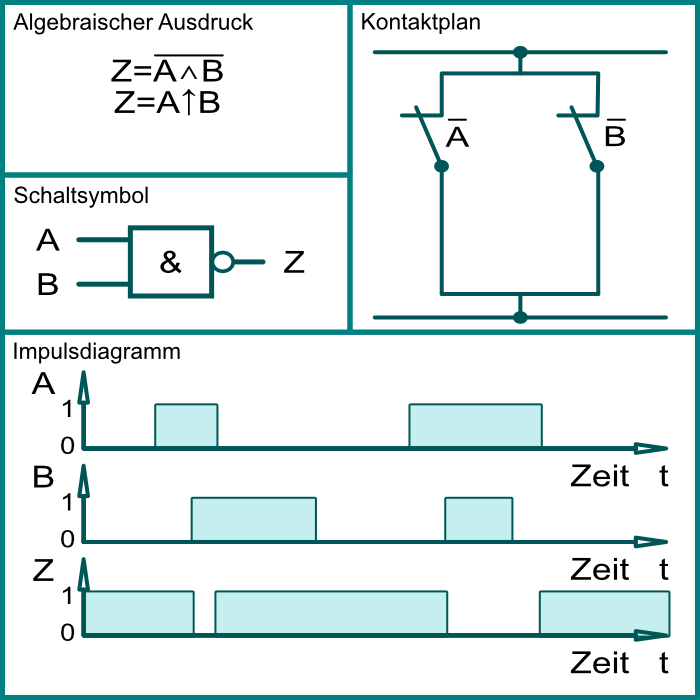
| Wahrheitstabelle | ||
| A | B | Z |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Die Ausgangsvariable ist WAHR wenn eine der Eingangsvariablen nicht WAHR ist.
Peircfunktion (NICHT ODER-NOR) ↓
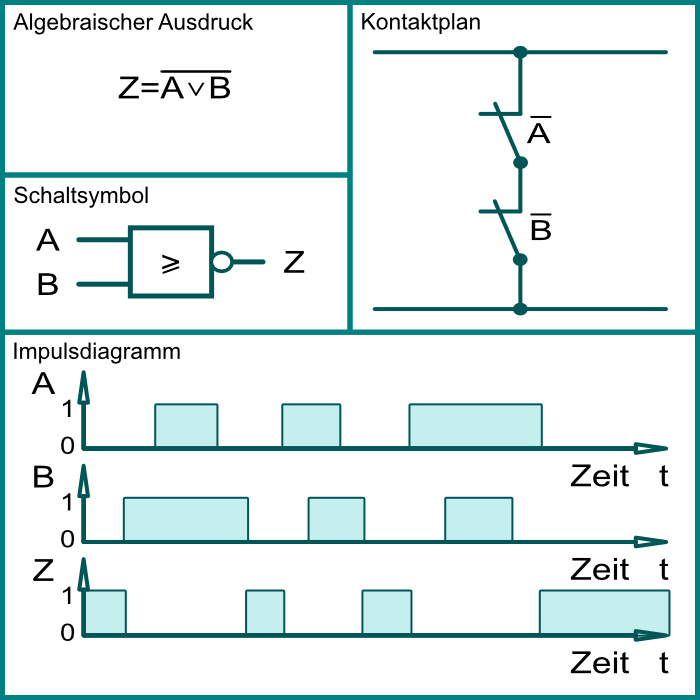
| Wahrheitstabelle | ||
| A | B | Z |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Die Ausgangsvariable ist WAHR wenn alle Eingangsvariablen FALSCH sind.
Beispiel Rundtisch
Ein Rundtisch hat einen Einpresszylinder, der von einem Kolben bewegt wird. An dem Tisch befinden sich 3 Taster (SF1, SF2 und SF3). Werden mindestens 2 Taster gleichzeitig bewegt, fährt der Kolben aus. Hat der Zylinder die erforderliche Einpresstiefe erreicht (BG2), fährt der Zylinder wieder zurück. Ein Neustart des Vorgangs kann erst erfolgen, wenn sich der Kolben wieder in der oberen Endstellung befindet (BG1).
Vorüberlegung
Aus dem Text können wir lesen, dass der Vorgang immer dann gestartet werden kann, wenn mindestens zwei Taster (SF1, SF2 und SF3) gleichzeitig betätigt werden und der Kolben (BG1) sich in der oberen Endstellung befindet. Übersetzt bedeutet dies mindestens zwei Taster und der Kolben müssen den Zustand WAHR haben also eine 1. Dies können wir in eine Wertetabelle eintragen.
| Zeile | SF1 | SF2 | SF3 | BG1 | Ausgang | Algebraische Gleichung |
| 1 | 0 | 0 | 0 | 0 | 0 | – |
| 2 | 0 | 0 | 0 | 1 | 0 | – |
| 3 | 0 | 0 | 1 | 0 | 0 | – |
| 4 | 0 | 0 | 1 | 1 | 0 | – |
| 5 | 0 | 1 | 0 | 0 | 0 | – |
| 6 | 0 | 1 | 0 | 1 | 0 | – |
| 7 | 0 | 1 | 1 | 0 | 0 | – |
| 8 | 0 | 1 | 1 | 1 | 1 | |
| 9 | 1 | 0 | 0 | 0 | 0 | |
| 10 | 1 | 0 | 0 | 0 | 0 | |
| 11 | 1 | 0 | 1 | 0 | 0 | |
| 12 | 1 | 0 | 1 | 1 | 1 | |
| 13 | 1 | 1 | 0 | 0 | 0 | |
| 14 | 1 | 1 | 0 | 1 | 1 | |
| 15 | 1 | 1 | 1 | 0 | 0 | |
| 16 | 1 | 1 | 1 | 1 | 1 |
Anhand dieser Wertetabelle können wir nun einen Logikplan erstellen.
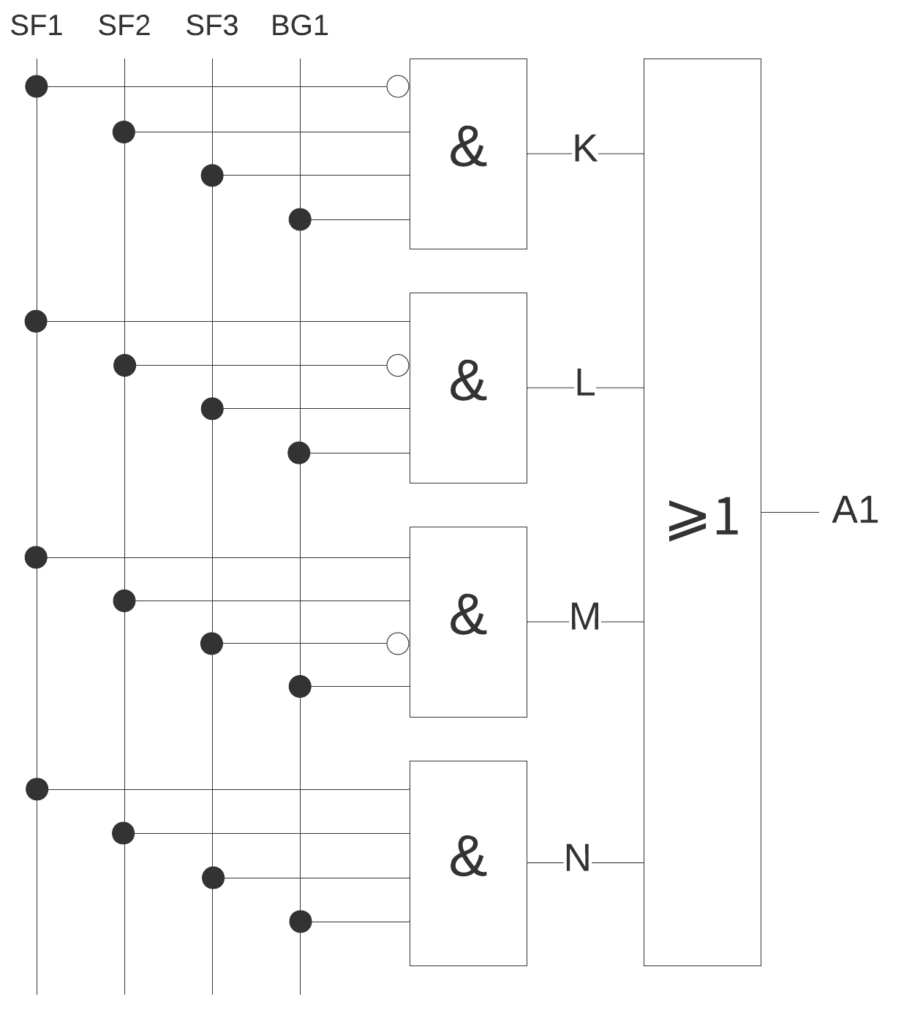
Es handelt sich hierbei um die Disjunktive Normalform (UND vor ODER). Diese ist sinnvoll, wenn weniger 1 als 0 in der Wertetabelle sind. Wäre es umgekehrt also weniger 0 als 1 dann wäre die Konjunktive Normalform (ODER vor UND) die bessere Wahl.
Beispiel Lüfterüberwachung
In einer Tiefgarage sind vier Lüfter installiert. Die Funktionsüberwachung erfolgt durch je einen Luftströmungswächter (E1-E4) An der Einfahrt der Tiefgarage ist eine Ampel angebracht. Sind alle vier Lüfter oder drei Lüfter in Betrieb, so ist für eine ausreichende Belüftung gesorgt und die Ampel zeigt grün (Ausgang A3). Bei Betrieb von nur zwei Lüftern schaltet die Ampel auf gelb (Ausgang A2). Sind weniger als zwei Lüfter in Betrieb, muss die Ampel rot (Ausgang A1) anzeigen.
Vorüberlegung
Aus dem Text lesen wir heraus, dass der Ausgang A3 immer dann 1 ist wenn mindestens 3 Eingänge gleichzeitig 1 sind. Sind genau zwei Lüfter aktiv schaltet die Ampel auf gelb. Denn 3 oder mehr sind grün und weniger als 2 sind schon rot.
| Zeile | E1 | E2 | E3 | E4 | A1 | A2 | A3 |
| 1 | 0 | 0 | 0 | 0 | 1 | ||
| 2 | 0 | 0 | 0 | 1 | 1 | ||
| 3 | 0 | 0 | 1 | 0 | 1 | ||
| 4 | 0 | 0 | 1 | 1 | 1 | ||
| 5 | 0 | 1 | 0 | 0 | 1 | ||
| 6 | 0 | 1 | 0 | 1 | 1 | ||
| 7 | 0 | 1 | 1 | 0 | 1 | ||
| 8 | 0 | 1 | 1 | 1 | 1 | ||
| 9 | 1 | 0 | 0 | 0 | 1 | ||
| 10 | 1 | 0 | 0 | 1 | 1 | ||
| 11 | 1 | 0 | 1 | 0 | 1 | ||
| 12 | 1 | 0 | 1 | 1 | 1 | ||
| 13 | 1 | 1 | 0 | 0 | 1 | ||
| 14 | 1 | 1 | 0 | 1 | 1 | ||
| 15 | 1 | 1 | 1 | 0 | 1 | ||
| 16 | 1 | 1 | 1 | 1 | 1 |
KV-Diagramm
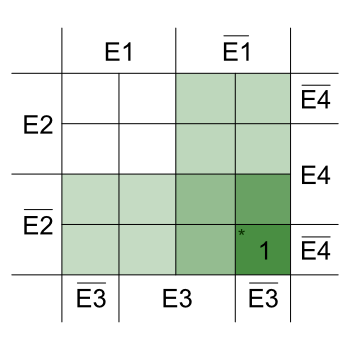
Das sogenannte KV-Diagramm soll dabei helfen die aus der Tabelle resultierenden Ergebnisse zu minimieren. Das KV Diagramm ist so zu beschriften, dass jede Variable und jede negierte Variable ein mal auf einander treffen können. In unserem Fall haben wir 4 Eingänge, es ergeben sich also 4^4 = 16 mögliche Kombinationen.
Um es auszufüllen liest man die Werte einfach aus der Wertetabelle ab und setzt die 1 da wo sie auskommt, wenn alle Bedingungen erfüllt sind. eine 0 steht dabei für „nicht“.
Beispiel anhand der ersten 1 in der Spalte A1. Ich habe die möglichen Bereiche grün markiert. Alle Eingänge sind negiert. Zunächst schaut man wo E1 negiert ist, dann wo E2 negiert ist. Diese Bereiche überlagern sich in einer Schnittmenge, der Bereich wird kleiner also dunkler, da zwei Bereiche übereinander liegen. Wo E3 negiert ist wird der Bereich nochmal kleiner und dunkler und E4 negiert hat schließlich nur noch 1 einziges Feld und da setzen wir eine 1 hin.
Ausgang A1
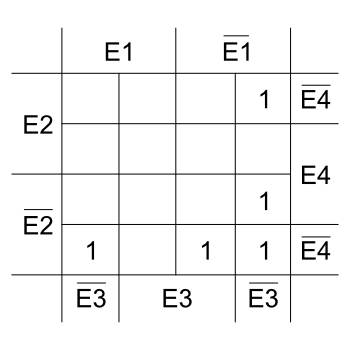
Nun bilden wir Gruppen aus den 1 die so groß wie möglich sind. Allerdings dürfen nur Gruppen gebildet werden, deren Anzahl an 1 eine Zweierpotenz ist. Also 2, 4, 8, 16, 32 usw.
Die Gruppen dürfen den Rand des Diagramms verlassen um auf der gegenüberliegenden Seite verwendet zu werden.
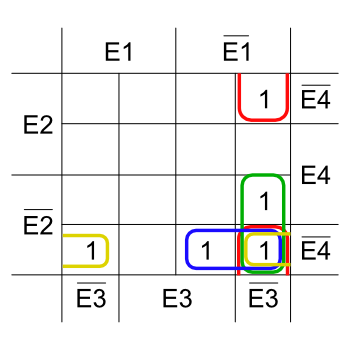
Aus diesen Gruppen kann man wiederum Gleichungen ableiten. Wobei die Eingänge so notiert werden, wie sie auch schon beim Eintragen abgelesen wurden. Eingänge die sowohl negiert als auch nicht negiert vorkommen heben sich auf und werden nicht notiert.
Das KV Diagramm kann man auf die selbe Weise für die Ausgänge A2 und A3 wiederholen und daraus weitere Schlüsse ziehen. z.B. einen Logikplan oder Kontaktplan zeichnen.

Einfach nur phänomenal, was Du da mit den Darstellungen der Logikverknüpfungen geleistet hast. Ultra verständlich.
Vielen vielen Dank dafür Nils!
Ich wünschte es würde mehr von Deiner Sorte geben!
Hallo Andi,
es freut mich, wenn ich dir damit helfen konnte! Vielen Dank für das Feedback!
Hallo,
ich glaube, dass Ihnen bei der Wahrheitstabelle der NOR-Verknüpfung ein kleiner Fehler unterlaufen ist. Hier steht die Wahrheitstabelle der AND-Verknüpfung.
Mit freundlichen Grüßen
Aaron
Vielen Dank für den Hinweis, habe ich korrigiert.
Informative Seite.
Beim Impulsdiagramm der Schefferfunktion (NICHT UND-NAND) ist im Z Diagramm fast am Ende ein kleiner Fehler.
Danke für den Hinweis, werde ich korrigieren! 🙂