Integralrechnung

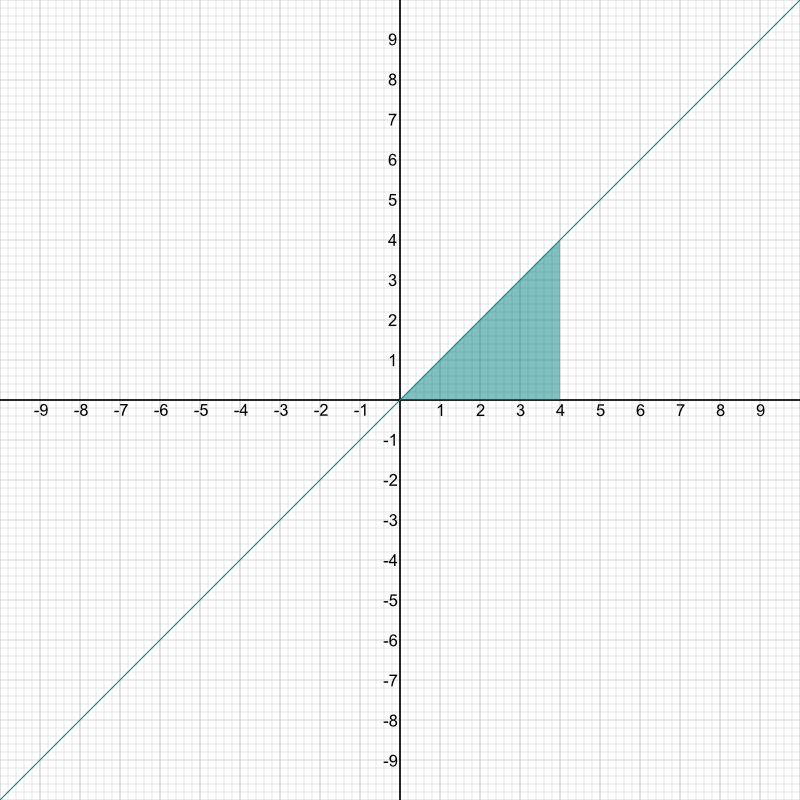
Die Integralrechnung dient dazu den Flächeninhalt unter einer Kurve zu ermitteln. Ein einfaches Beispiel wäre dieses:

Gerade

Der Basis der Integralrechnung ist die Funktion.

$\inline \LARGE f(x)=x$

Das Zeichen für die Integralrechnung ist folgendes ∫. Unterhalb des Integralzeichens steht die untere Grenze und oberhalb die obere Grenze der X-Achse (Horizontale). In unserem Fall also 0 – 4. Hinter dem Inegral kommt die Funktion. Also x und um das Integral zu schließen wird die Zeichenfolge dx verwendet.

$\LARGE \int_{o}^{4}x\: dx$

Von diesem Integral möchten wir nun die Stammfunktion bilden (aufleiten). Anders als beim ableiten, erhöhen wir jedoch die Potenz von x. Da dort keine Potenz steht, hat x eine Potenz von 1. Nach dem integrieren hat x also eine Potenz von 2. Vor dem x schreiben wir das, was vor dem x steht. Da in unserem Fall nichts vor dem x steht, ist dieser Wert ebenfalls 1. Dann wird durch die Potenz von x geteilt.

$\LARGE \int_{0}^{4}x\: dx = \left [ \frac{1}{2}\cdot x^{2} \right ]_{0}^{4}$

Nun können wir einsetzen. Der Bruch bleibt bestehen, für x setzen wir zuerst die obere Grenze unserer Stammfunktion ein. Dann wird der Bruch mit der unteren Grenze und der Potenz subtrahiert.

$\LARGE \int_{0}^{4}x\: dx = \left [ \frac{1}{2}\cdot x^{2} \right ]_{0}^{4}=\frac{1}{2}\cdot 4^{2}-\frac{1}{2}\cdot 0^{2}=8$

Wenn wir das mal mit Pythagoras oder den Winkelfunktionen überprüfen stellen wir fest, dass es passt. Zugegeben für diese Funktion würde man kein Integral aufstellen, ich wollte nur zeigen, wie es funktioniert.