Definition
Im zentralen Kräftesystem gehen alle Kräfte durch einen Punkt (Deswegen Zentral). Im zentralen Kräftesystem gibt es keine Kraftmomente. Im allgemeinen Kräftesystem jedoch schon. Wenn eine Kraft F unter einem gewissen Wirkabstand l auf einen Bezugspunkt wirkt so entsteht ein Moment M.
Der Wirkabstand wird stets rechtwinklig zur Kraft angegeben.
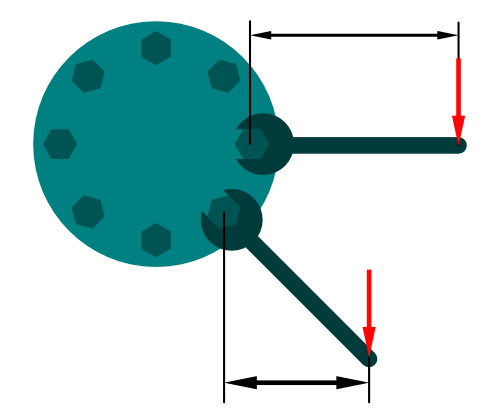
In diesem Beispiel wird deutlich, wie sich das Kraftmoment verändert, wenn der Winkel sich verändert unter dem eine Kraft auf einen Hebel wirkt. Wirkt diese nicht orthogonal auf den Hebel, so verringert sich der Wirkabstand und das Kraftmoment wird geringer.
Zusätzlich zum zentralen Kräftesystem erhalten wir also noch die Momente als zusätzlich zu berücksichtigen Faktor. Daraus resultiert: Der Körper ist dann im Gleichgewicht, wenn die Summe aller Kräfte sowohl in X, als auch in Y Achse = 0 sind und die Summe aller Momente = 0 ist.
- ΣFX = 0 = ….
- ΣFY = 0 = ….
- ΣM(…) = 0 = ….
In den Klammern der Momente geben wir den Bezugspunkt an. Nur wenn dieser angegeben wird, kann die Rechnung nachvollzogen werden.
Beispiel 1
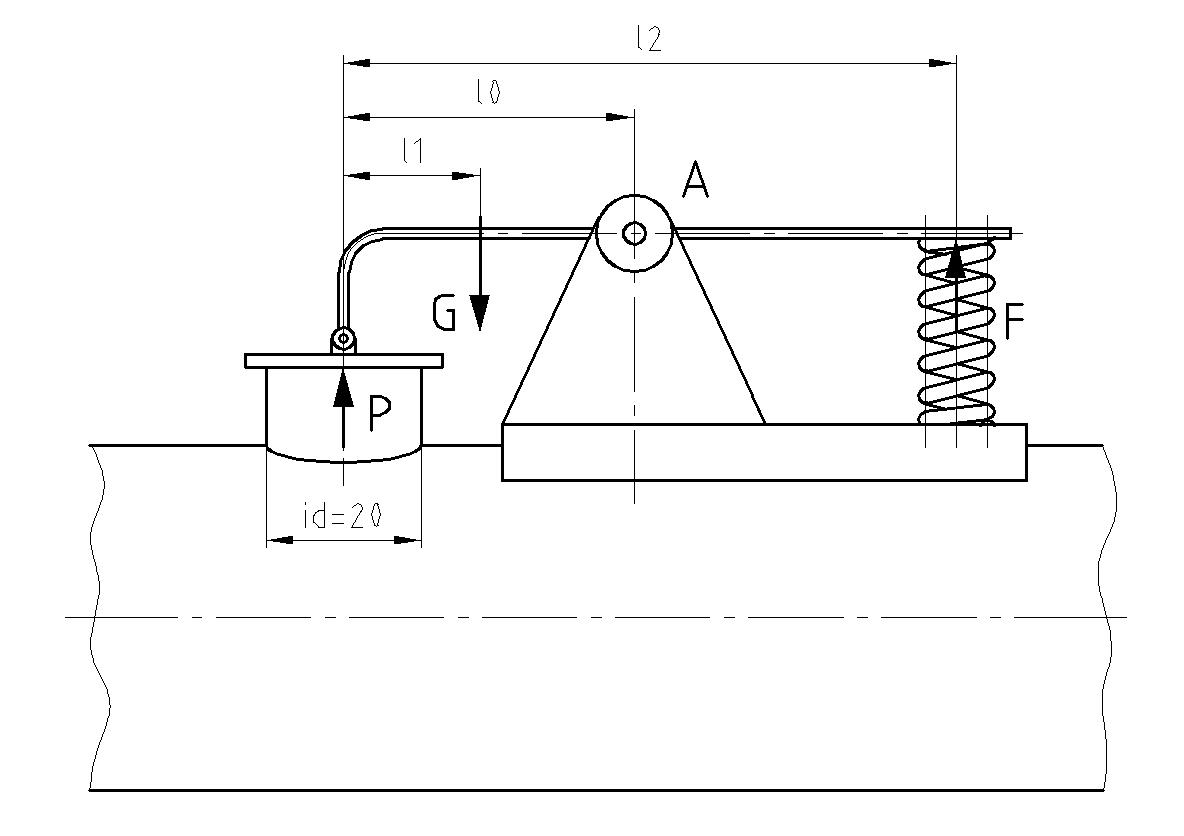
Der Blindflansch des Stutzens hat inklusive des Sicherungsmechanismus eine Gewichtskraft FG von 11 N. Der Hebel, der am Deckel befestigt ist wird durch eine Feder mit der Druckkraft F von 50 N gegen den Stutzen gedrückt. Der Stutzen hat einen lichten Durchmesser d von 20 mm. Der Drehpunkt des Hebels ist so zu legen, dass der Deckel bei p = 6 · 105 Pa Überdruck in der Rohrleitung öffnet. Die Abstände sind: l1 = 90 mm und l2 = 225 mm.
a)
Mit welcher Kraft wird das Lager A belastet?
Als erstes schneiden wir das System frei.
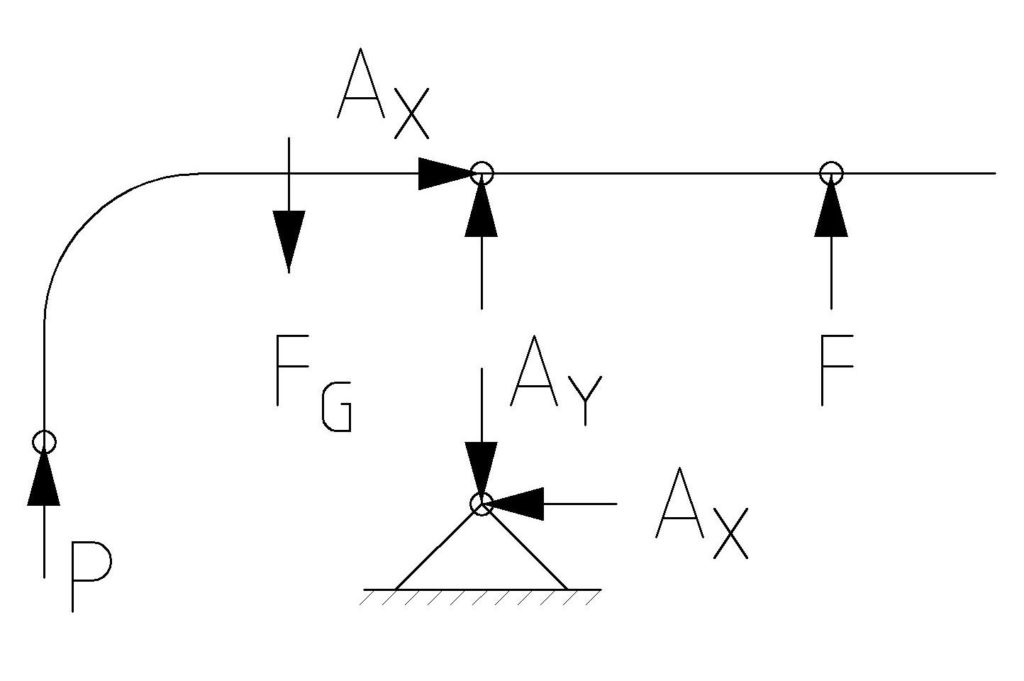
Zunächst einmal brauchen wir den Betrag der Kraft P. Wir haben den Innendurchmesser des Stutzens mit 20 mm gegeben. Außerdem kennen wir den herrschenden Innendruck p von 6 bar.
1 bar = 0,1 N / mm²
Wir sehen also, dass wir die Querschnittsfläche in mm² benötigen um die Kraft in N zu erhalten. Diese rechnen wir aus:
Anhand der Fläche können wir nun unsere Kraft errechnen.
Den Betrag der Resultierenden A zu errechnen ist nun einfach, da alle angreifenden Wirklinien parallel zueinander verlaufen, brauchen wir die Käfte nun bloß noch anhand ihrer Vorzeichen addieren bzw. subtrahieren. Das Vorzeichen hängt davon ab ob die Kraft nach oben oder nach unten zeigt. Nicht zu verwechseln mit dem Momentendrehsatz, wo das Vorzeichen anhand der Drehrichtung festgelegt wird.
b)
Welcher Abstand l0 muss gewählt werden?
Wir stellen die Momentengleichung auf und stellen diese nach l0 um.
Um l0 besser ausklammern zu können, schreibe ich die Gleichung um, indem ich die Klammern auflöse. Die Klammern werden aufgelöst indem jeder Wert in der Klammer mit dem Faktor multipliziert wird. Dabei unbedingt auf die Vorzeichen achten.
Nun bringe ich alle Terme ohne l0 auf die andere Seite.
Nun klammere ich l0 aus.
