Torsion

Während man bei der Biegung üblicherweise von Balken oder Trägern spricht, so redet man bei Torsion eher von Stäben.  Torsion ist die Beanspruchung auf Verdrehung um die Stabachse herum.

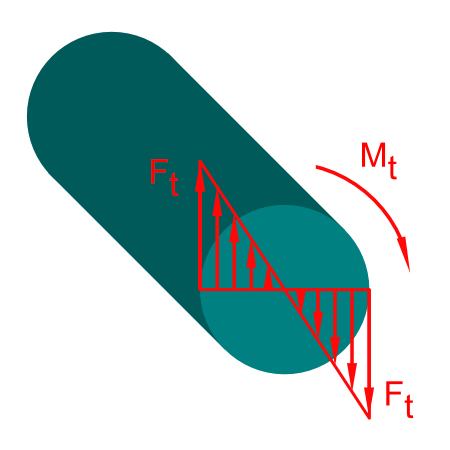
Die Torsion ist dabei linear auf dem Querschnitt verteilt. Dabei erträgt die Mantelfläche die größte Spannung während die Stabachse nicht verformt wird.

Torsion ist abhängig von der Elastizität der Werkstoffe.

• Bei Normalspannungen σ (Zug, Druck, Biegung) wird diese durch den Elastizitätsmodul E dargestellt. Bei Stahl beträgt er ca. 210.000 N/mm²
• Bei Schubspannungen τ (Torsion) ist die Kenngröße für die Elastizität der Schubmodul G welcher bei Stahl bei ca. 81.000 N/mm² liegt.

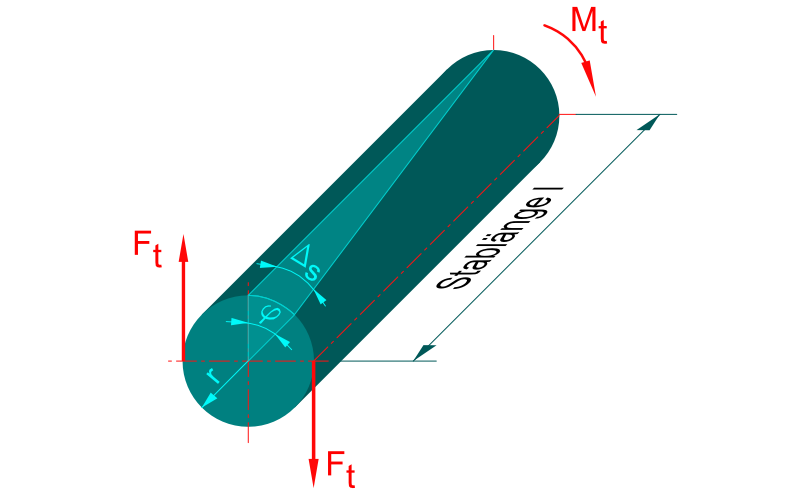
Formelzeichen Torsion

RM = Roloff Matek
FS = Formelsammlung
TB = Tabellenbuch

Formeln Torsion

Torsionsspannung

$$\begin{gathered} {\tau }_t=\frac{M_t}{W_p} (Für die Mantelfläche) \\ {\tau }_t=\frac{M_t·r}{I_p} (Für Radius r) \end{gathered}$$

Widerstandsmoment

$W_p=\frac{I_p}{r}$

Erforderliches Widerstandsmoment

$W_{perf}=\frac{M_{tmax}}{{\tau }_{tzul}}$

zulässige Torsionsspannung

$$\begin{gathered} {\tau }_{tzul}=\frac{{\tau }_{tF}}{\nu } (bei zähhen Werkstoffen) \\ {\tau }_{tzul}=\frac{{\tau }_{tB}}{\nu } (bei spröden Werkstoffen) \end{gathered}$$

Maximales Torsionsmoment

$M_{tmax}={\tau }_{tzul}·W_p$

Sicherheitszahl

$$\begin{gathered} \nu =\frac{{\tau }_{tF}}{{\tau }_t} (bei zähen Werkstoffen) \\ \nu =\frac{{\tau }_{tB}}{{\tau }_t} (bei spröden Werkstoffen) \end{gathered}$$

Verdrehwinkel

$$\begin{gathered} \phi =\frac{{\tau }_t·l}{G·r}·\frac{180°}{\pi } \\ \phi =\frac{M_t·l}{W_p·r·G}·\frac{180°}{\pi } \\ \phi =\frac{M_t·l}{I_p·G}·\frac{180°}{\pi } \end{gathered}$$

Als Erfahrungswert hat sich 0,25 ° / Meter herausgestellt.

erforderlicher Durchmesser (Bei Kreisquerschnitt)

$d_{erf}=\sqrt[3]{\frac{16·M_t}{\pi ·{\tau }_{tzul}}}$

Torsionsmoment

$$\begin{gathered} M_t=F·r \\ {M}_t=9550·\frac{P}{n} \left(Zahlenwertgleichtung\right) \end{gathered}$$

Drehmoment M_t in Nm
Drehzahl n in min^-1
Leistung P in kW

Vollwelle oder Hohlwelle?

Das folgende Beispiel soll zeigen, dass Hohlwellen gegenüber Vollwellen deutliche Vorteile aufweisen. Dafür vergleichen wir zwei Wellen. Eine Vollwelle mit 40 mm Durchmesser und eine Hohlwelle mit einem Außendurchmesser von 70 mm und einem Innendurchmesser von 57 mm. Beide werden mit einem Torsionsmoment M_t = 700 Nm belastet.

Berechnung der Vollwelle

Wir erinnern uns die Formel für die Grundbeanspruchung Torsion ist ähnlich die der Biegung. Nur das Schubspannungen mit τ statt σ angegeben werden und der Index nicht b sondern t it.

${\tau }_t=\frac{M_t}{W_t}$

Jetzt können wir W_t allerdings nicht aus ein einer Tabelle ablesen, da es sich bei Wellen ja nicht um Normteile handelt. Stattdessen setzen wir die Formel für die Berechnung von W_t von zylindrischen Vollprofilen ein. (Siehe Roloff Matek T 11-3)

$$\begin{gathered} \frac{\mathrm{\pi }}{16}·d^3 |einsetzen in Formel \\ {\tau }_t=\frac{M_t·16}{\mathrm{\pi }·{\mathrm{d}}^3} \\ {\tau }_t=\frac{700000 Nmm ·16}{\mathrm{\pi }·{(40 mm)}^3}=55,7 N/m{m}^2 \end{gathered}$$

Berechnen der Hohlwelle

Hier nutzen wir die selbe Methode, nur dass wir die Formel W_t für zylindrische Hohlprofile nutzen.

$$\begin{gathered} \frac{\mathrm{\pi }}{16}·\frac{D^4–d^4}{D} |einsetzen in Formel \\ {\tau }_t=\frac{M_t·16·D}{\mathrm{\pi }·({\mathrm{D}}^4–{\mathrm{d}}^4)} \\ {\tau }_t=\frac{700000 Nmm·16·70 mm}{\mathrm{\pi }·({(70 mm)}^4–{(57 mm)}^4)}= 18,55 N/m{m}^2 \end{gathered}$$

1. Vergleich

Wir stellen fest, dass die Hohlwelle eine deutlich geringere Spannung aufweist. Aber liegt das nicht nur daran, dass der Durchmesser größer ist und sie mehr Querschnittsfläche hat?

Berechnen der Querschnitte

Vollwelle

$$\begin{gathered} A=\frac{\mathrm{\pi }·{\mathrm{d}}^2}{4} \\ A=\frac{\mathrm{\pi }·{(40 \mathrm{mm})}^2}{4}= 1256 m{m}^2 \end{gathered}$$

Hohlwelle

$$\begin{gathered} A=\frac{\mathrm{\pi }·({\mathrm{D}}^2–{\mathrm{d}}^2)}{4} \\ A=\frac{\mathrm{\pi }·\left({\left(70 \mathrm{mm}\right)}^2–{\left(57 \mathrm{mm}\right)}^2\right)}{4}=1297 m{m}^2 \end{gathered}$$

2. Vergleich

Vergleichen wir nun die Spannungsunterschiede im Vergleich zu den Unterschieden der Querschnitte.

$$\begin{gathered} {\%}_{{Abweichung}_S}=\frac{(55,7 N/m{m}^2 – 18,55 N/m{m}^2)}{55,7 N/mm²}·100\% = 66,7 \% \\ {\%}_{{Abweichung}_A}=\frac{(1297 m{m}^{2 }– 1256 m{m}^2)}{1256 mm²}·100\% = 3,26 \% \end{gathered}$$

Fazit

Bei nur extrem geringen Querschnittabweichungen, kann die Spannung erheblich gesenkt werden. Bei gleichem Gewicht können Hohlwellen größere Drehmomente übertragen bzw. Bei einem gegebenem Drehmoment können Hohlwellen deutlich leichter dimensioniert werden. Dies liegt unter anderem daran, dass die neutrale Faser spannungsfrei ist und die Spannungen vorrangig im Randbereich auftreten.

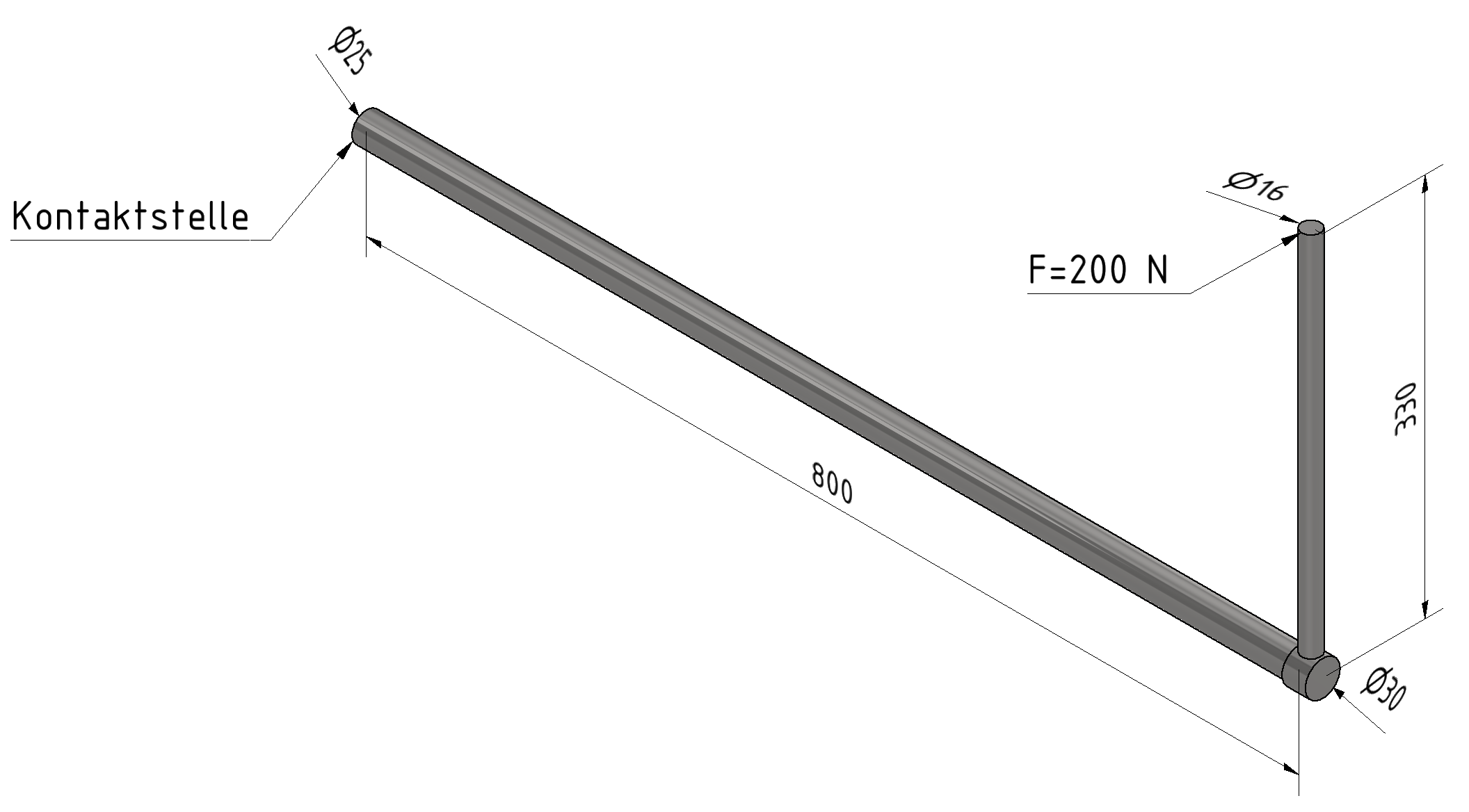
Beispiel 1: Hebel

Hier wird vorerst nur die Torsion betrachtet, auch wenn natürlich auch andere Beanspruchungen auftreten wie z.B. die Biegung

Das Bild zeigt die stark vereinfachte Skizze eines Hebels. Dieser ist an der Kontaktstelle eingespannt.

1. Die erste Aufgabe besteht darin zu überprüfen, ob die Hebelstange d = 25 mm nicht auch aus dünnerem Rundstahl ausgeführt werden kann.
2. Welcher Durchmesser muss mindestens genommen werden?
3. Ist das Ergebnis realistisch? Welche Reaktionen würden bei Benutzung des Hebels wahrscheinlich auftreten?
4. Wie kann das Ergebnis überprüft werden, ohne das ein Experiment durchgeführt werden muss?

1) Zunächst ermitteln wir das Torsionsmoment

$M_t=F·l = 200 N · 330 mm = 66000 Nmm$

Dann ermitteln wir welche Spannung für das angenommene Material (S235JR) zulässig ist und legen 1,5 als Sicherheitsfaktor fest.

${\tau }_{tzul}=\frac{{\tau }_{tSchN}}{\nu }=\frac{165 N}{mm²·1,5}=110 N/mm²$

Nun benötigen wir den erforderlichen Durchmesser. Dafür formen wir die Grundformel für die Torsionsbeanspruchung etwas um.

${\tau }_t=\frac{M_t}{W_p}$

Für W_p setzen wir die Formel für W_p bei Kreisquerschnitten ein. (Roloff Matek T 11-3).

${\tau }_t=\frac{M_t·16}{\mathrm{\pi }·d^3}$

Diese stellen wir nun nach d um.

$$\begin{gathered} {\tau }_t=\frac{M_t·16}{\mathrm{\pi }·d^3} |·(\mathrm{\pi }·{\mathrm{d}}^3) \\ {\tau }_t·\mathrm{\pi }·{\mathrm{d}}^3={\mathrm{M}}_{\mathrm{t}}·16 |÷({\mathrm{\tau }}_{\mathrm{t}}·\mathrm{\pi }) \\ {\mathrm{d}}^3=\frac{{\mathrm{M}}_{\mathrm{t}}·16}{{\mathrm{\tau }}_{\mathrm{t}}·\mathrm{\pi }} |\sqrt[3]{} \\ \mathrm{d}=\sqrt[3]{\frac{{\mathrm{M}}_{\mathrm{t}}·16}{{\mathrm{\tau }}_{\mathrm{t}}·\mathrm{\pi }}} = \sqrt[3]{\frac{66000 Nmm · 16 · mm²}{110 N · \mathrm{\pi }}} =14,51 mm \end{gathered}$$

gewählt: 15 mm

Vergleichen wir nun die beiden Querschnittsflächen.

$$\begin{gathered} A_V=\frac{{(25 mm)}^2·\mathrm{\pi }}{4} =490,84 mm² \\ {A}_N=\frac{{(15 mm)}^2·\mathrm{\pi }}{4} =176,71 mm² \\ {A}_V–A_N = 314,13 mm² \end{gathered}$$

Das entspricht einer Materialersparnis von 64 % !

Formänderung

schauen wir uns nun an wie stark sich der Stab verformen würde.

$$\begin{gathered} \phi =\frac{M_t·l}{I_t·G}·\frac{180°}{\pi } \\ Wir setzen die Formel für das Flächenmoment 2.Grades ein. \\ Alternativ könnte man I_{t_{}}natürlich auch vorher ausrechnen. \\ {I}_t=\frac{\mathrm{\pi }}{32}·d^4 \\ \phi =\frac{M_t·l·32}{\mathrm{\pi }·{\mathrm{d}}^4·\mathrm{G}}·\frac{180°}{\pi } \\ \phi =\frac{66000 \cancel{\cancel{\cancel{N}}mm}·800 \cancel{mm}· 32 · \cancel{m{m}^2}}{\mathrm{\pi }·{15}^4 m{m}^4·81000 \cancel{N}}·\frac{180°}{\pi } \\ \phi =7,515° \end{gathered}$$

Um zu sehen wie stark sich die Welle nun in Millimeter verformt rechnen wir die Bogenlänge am Umfang aus.

$$\begin{gathered} l_B=\frac{\mathrm{\pi }·\mathrm{d}·\mathrm{\phi }}{360°} \\ {l}_B=\frac{\mathrm{\pi }·15 \mathrm{mm}·7,515\cancel{°}}{360\cancel{°}} \\ {l}_B=0,984 mm \end{gathered}$$

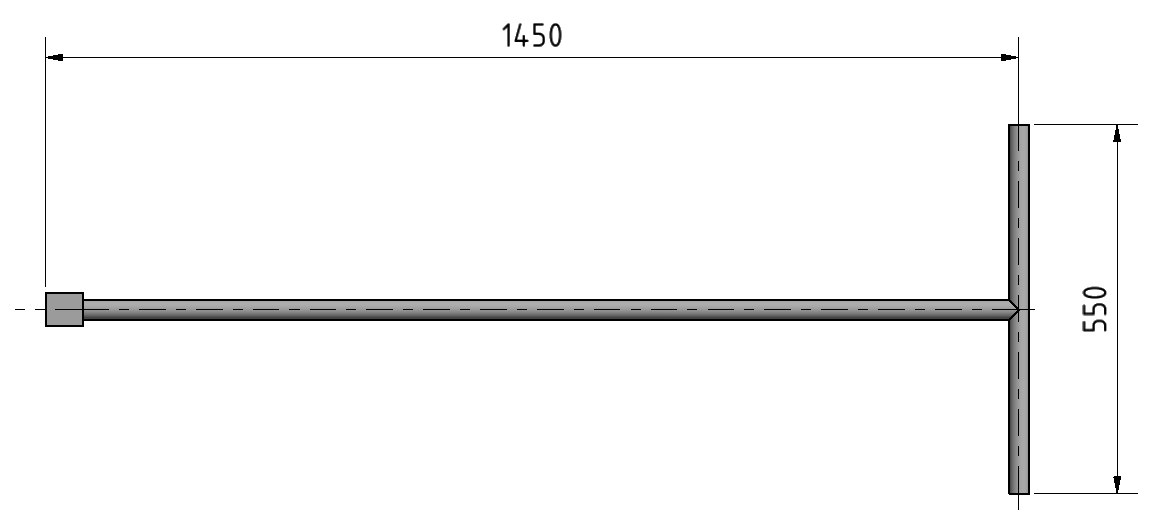
Beispiel  2: Hydrantenschlüssel

Hier nehmen wir vereinfachend an, dass der Schlüssel durchgehend gleich dick ist. Die Handkraft beträgt je Seite 200 N. Wir entscheiden uns für einen Werkstoff mit der Schwellfestigkeit von 100 N/mm².

Auch hier ermitteln wir zunächst das wirkende Tosionsmoment.

$$\begin{gathered} M_t=F·l \\ {M}_t=275 mm · 200 N · 2 \\ {M}_t=110000 Nmm \end{gathered}$$

Nun ermitteln wir wieder die zulässige Torsionsspannung. Dieses mal nehmen wir eine Sicherheit von 3 an.

$$\begin{gathered} {\tau }_{tzul}=\frac{{\tau }_{tSchN}}{\nu } \\ {\tau }_{tzul}=\frac{100 N}{m{m}^2·3} \\ {\tau }_{tzul}=33,3\overline{3} N/mm² \end{gathered}$$

Nun ermitteln wir den Durchmesser

$\mathrm{d}=\sqrt[3]{\frac{{\mathrm{M}}_{\mathrm{t}}·16}{{\mathrm{\tau }}_{\mathrm{t}}·\mathrm{\pi }}} = \sqrt[3]{\frac{110000 Nmm · 16 · mm²}{33,3\overline{3} N · \mathrm{\pi }}} =25,62 mm$

Beispiel 3: Getriebewelle

Eine Getriebewelle aus E295 mit einer Drehzahl von n = 112 min^-1 soll in einem Getriebe eine Leistung von P = 3 kW übertragen.

1. Welcher Wellendurchmesser ist zu wählen, wenn die zulässige Torsionsspannung nicht überschritten werden darf?
2. Wie groß muss der Wellendurchmesser sein, wenn der Verdrehwinkel φ von 0,25°/m nicht überschritten werden darf?

Hinweis: wir führen hier einen vereinfachten (überschlägigen) Festigkeitsnachweis durch.

Aufgabe 1

Zunächst einmal stellen wir fest, dass die zulässige Torsionsspannung der Quotient aus Festigkeit des Werkstoffes und des Sicherheitsfaktors ν ist. Für den Festigkeitswert nehmen wir τ_tSchN da die Torsion hier ein schwellender Lastfall ist.

$$\begin{gathered} {\tau }_{tzul}=\frac{{\tau }_{tSchN}}{\nu } (ähnlich RM FS 3–55) \\ {\tau }_{tzul}=\frac{205}{1,5}=136,6\overline{6} \end{gathered}$$

halten wir nun die Grundformel für Torsionsbeanspruchung fest. Da wir gegen die zulässige Torsionsspannung rechnen wollen, setzen wir dies so ein.

${\tau }_t=\frac{M_t}{W_t} \Rightarrow {\tau }_{tzul}=\frac{M_t}{W_t} (RM FS 3–1)$

Jetzt kennen wir jedoch weder das Torsionsmoment M_t noch das Widerstandsmoment W_t. Da wir jedoch die Drehzahl und die Leistung kennen, können wir uns das Drehmoment anhand dieser Werte errechnen. Es gibt natürlich auch Zahlenwertgleichungen dafür. Ich möchte hier des Verständnisses wegen, aber den langen Weg zeigen.

$$\begin{gathered} M_t=\frac{P}{2·\mathrm{\pi }·\mathrm{n}} (RM FS 11–5) \\ {M}_t=\frac{3000 Nm · 60 \cancel{s}}{\cancel{s} ·2·\mathrm{\pi }·112} \\ {M}_t= 255,78 Nm \end{gathered}$$

Für P setzen wir 3000 Nm/s ein ( 1 W = 1 Nm/s). Bei der Drehzahl setzen wir 112 ein. Über dem Bruchstrich 60 s. Die Einheit für die Drehzahl ist ja min^-1 . Was 1/min bedeutet und um von Minuten auf Sekunden zu kommen multiplizieren wir mit 60.

Für W_t haben wir ebenfalls keinen Wert, da wir ja den Durchmesser noch nicht kennen. Wir können aber die Formel für die Ermittlung des Widerstandsmoments in die Gleichung einsetzen.

$W_t=\frac{\mathrm{\pi }}{16}·d^3$

$$\begin{gathered} {\tau }_{tzul}=\frac{M_t}{W_t} \\ {\tau }_{tzul}=\frac{M_t·16}{\mathrm{\pi }·{\mathrm{d}}^3} \end{gathered}$$

Jetzt können wir diese Gleichung nach d umstellen.

$$\begin{gathered} {\tau }_{tzul}=\frac{M_t·16}{\mathrm{\pi }·{\mathrm{d}}^3} |·\pi ·d^3 \\ {\tau }_{tzul}·\mathrm{\pi }·{\mathrm{d}}^3={\mathrm{M}}_{\mathrm{t}}·16 |÷\left({\mathrm{\tau }}_{\mathrm{tzul}}·\mathrm{\pi }\right) \\ {\mathrm{d}}^3=\frac{{\mathrm{M}}_{\mathrm{t}}·16}{{\mathrm{\tau }}_{\mathrm{tzul}}·\mathrm{\pi }} |\sqrt[3]{} \\ \mathrm{d}=\sqrt[3]{\frac{{\mathrm{M}}_{\mathrm{t}}·16}{{\mathrm{\tau }}_{\mathrm{tzul}}·\mathrm{\pi }}} \end{gathered}$$

In diese Gleichung setzen wir nun die Zahlenwerte ein.

$$\begin{gathered} \mathrm{d}=\sqrt[3]{\frac{255780 \cancel{N}mm·16·\cancel{mm²}}{136,6\overline{6} \cancel{N}·\mathrm{\pi }}} \\ d=21,2 mm \end{gathered}$$

Jetzt wählen wir anhand DIN 323 den nächst passenden Normdurchmesser.

d_gew = 22,4 auch möglich aber sehr knapp, wäre genau 21,2 mm

Aufgabe 2

Jetzt versuchen wir zu ermitteln wie groß der Durchmesser sein müsste, wenn der Verdrehwinkel von 0,25°/m nicht überschritten werden darf. Dabei gehen wir prinzipiell ähnlich vor. Zunächst notieren wir die Grundformel.

$\phi °=\frac{180}{\mathrm{\pi }}·\frac{M_t·l}{G·I_t}$

Auch hier setzen wir die Formel für I_t ein, wie wir es zuvor mit W_t getan haben.

$I_t=\frac{\mathrm{\pi }}{32}·d^4$

einsetzen und Bruch 180/π schon mal ausrechnen um einfacher umstellen zu können.

$\phi °=57,3°·\frac{M_t·l·32}{G·\mathrm{\pi }·{\mathrm{d}}^4}$

Diese Gleichung können wir nun umstellen.

$$\begin{gathered} \phi °=57,3°·\frac{M_t·l·32}{G·\mathrm{\pi }·{\mathrm{d}}^4} |·G·\mathrm{\pi }·{\mathrm{d}}^4 \\ \mathrm{\phi }°·\mathrm{G}·\mathrm{\pi }·{\mathrm{d}}^4=57,3°·{\mathrm{M}}_{\mathrm{t}}·\mathrm{l}·32 |÷(\mathrm{\phi }°·\mathrm{G}·\mathrm{\pi }) \\ {\mathrm{d}}^4=\frac{57,3°·{\mathrm{M}}_{\mathrm{t}}·\mathrm{l}·32}{\mathrm{\phi }°·\mathrm{G}·\mathrm{\pi }} |\sqrt[4]{} \\ \mathrm{d}=\sqrt[4]{\frac{57,3°·{\mathrm{M}}_{\mathrm{t}}·\mathrm{l}·32}{\mathrm{\phi }°·\mathrm{G}·\mathrm{\pi }}} \end{gathered}$$

Hier setzen wir nun wieder die bekannten Werte ein.

$$\begin{gathered} \mathrm{d}=\sqrt[4]{\frac{57,3°·255780 \cancel{N}mm·1000 \cancel{mm}·32·\cancel{m{m}^2}}{0,25°·81000 \cancel{N}·\mathrm{\pi }}} \\ d=52,11 mm \\ {d}_{gew}=53 mm \end{gathered}$$

Hier sieht man sehr gut wie stark der erforderliche Durchmesser anwächst, wenn die zulässige Verdrehung eingeschränkt wird. Ob eine Welle sich wie stark verdrehen darf, hängt von den Anforderungen ab.