Beanspruchung auf Biegung

Bei der Beanspruchung auf Biegung muss der Querschnitt eine Querkraft F_q und ein Biegemoment M_bübertragen. Das Biegemoment belastet den Querschnitt am stärksten. Es erzeugt die Biegespannung σ_b.

Formelzeichen

σ_b	Biegespannung [N/mm²]
M_b	Biegemoment Nmm]
W_b	axiales Widerstandsmoment [mm³]
σ_bzul	zulässige Biegespannung [N/mm²]
ν	Sicherheitszahl
W_erf	erforderliches axiales Widerstandsmoment [mm³]
σ_bF	Biegefließgrenze [N/mm²]
σ_bB	Biegefestigkeit [N/mm²]
M_bmax	maximales Biegemoment [Nmm]
d_erf	erforderlicher Durchmesser [mm](bei Kreisquerschnitten)
f	Durchbiegung [mm]
σ_zmax	größte Zugspannung [N/mm²]
σ_dmax	größte Druckspannung [N/mm²]
e₁,e₂	Randfaserabstände [mm]
I	Flächenmomenträgheitsmoment [mm⁴]
F	Kraft [N]
F‘	Streckenlast [N/mm]
l, a, b	Längenmaße [mm]
E	Elastizitätsmodul [N/mm²]

Formeln

Biegespannung

Bei der Biegebelastung ist die Biegespannung der Maximalwert.

$σ_{b} = \frac{M_{b}}{W_{b}}$

maximales Biegemoment

$M_{b m a x} = σ_{b z u l} \cdot W$

Erforderliches Widerstandsmoment

Das Widerstandsmoment wird aus dem Querschnitt des Werkstückes ermittelt. Für genormte Stahlprofile liegen die Widerstandsmomente in Form von Tabellenbüchern etc. vor und können abgelesen werden. Für andere Profilformen kann dies rechnerisch ermittelt werden.

$W_{e r f} = \frac{M_{b m a x}}{σ_{b z u l}}$

Sicherheitszahl

$ν = \frac{σ_{b F}}{σ_{b}} b z w . ν = \frac{σ_{b B}}{σ_{b}}$

zulässige Biegespannung

$σ_{b z u l} = \frac{σ_{b F}}{ν} (b e i z ä h e n W e r k s t o f f e n) σ_{b z u l} = \frac{σ_{b B}}{ν} (b e i s p r ö d e n W e r k s t o f f e n)$

erforderlicher Durchmesser (Kreisquerschnitt)

$d_{e r f} = \sqrt[3]{\frac{32 \cdot M_{b m a x}}{π \cdot σ_{bzul}}}$

Spannungsverteilung in unsymmetrischen Querschnitten

Größte Zugspannung

$σ_{z m a x} = \frac{M_{b} \cdot e_{1}}{I}$

Größte Druckspannung

$σ_{d m a x} = \frac{M_{b} \cdot e_{2}}{I}$

Methode 1 – Querkraftverlauf

Freiträger mit Einzellast

F = 100 N
l = 120 mm

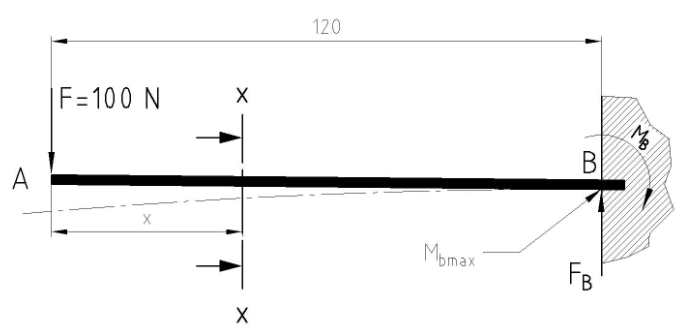
Bei Freiträgern mit Einzellast gilt: M_bmax= F · l (in diesem Fall 120 mm)

$M_{b m a x} = F \cdot l M_{b m a x} = 100 N \cdot 120 m m M_{b m a x} = 12000 N m m = 12 N m$

Freiträger mit mehreren Einzellasten

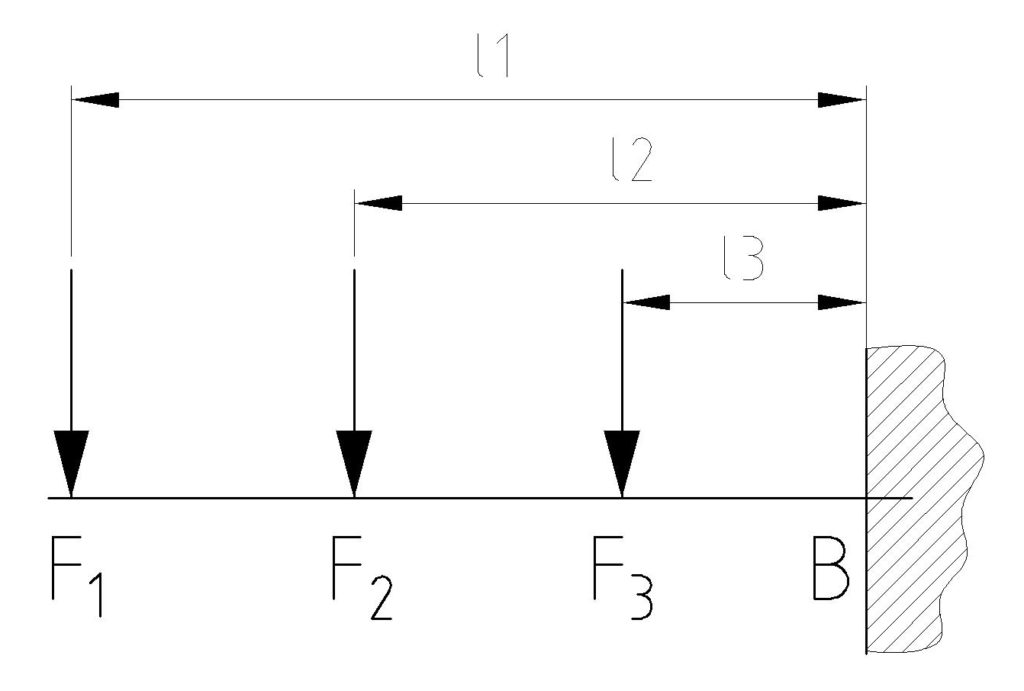
Bei einem Freiträger mit mehreren Einzellasten ist das maximale Biegemoment die Summe aller Momente der Einzellasten.

$M_{b m a x} = M_{B} = F_{1} \cdot l_{1} + F_{2} \cdot l_{2} + F_{3} \cdot l_{3}$

Stützträger (Kragträger) mit mehreren Einzellasten

Bei Stützträgern mit mehreren Einzellasten wird es langsam etwas komplizierter. Hier genügt es nicht mehr die Momente zu addieren. Für die Berechnung benötigen wir ein Querkraftverlauf bzw. F_q,x-Diagramm.

F₁ = 25 kN
F₂ = 10 kN
F₃ = 20 kN

l = 6 m
l₁ = 2,5 m
l₂= 2 m
l₃ = 1 m

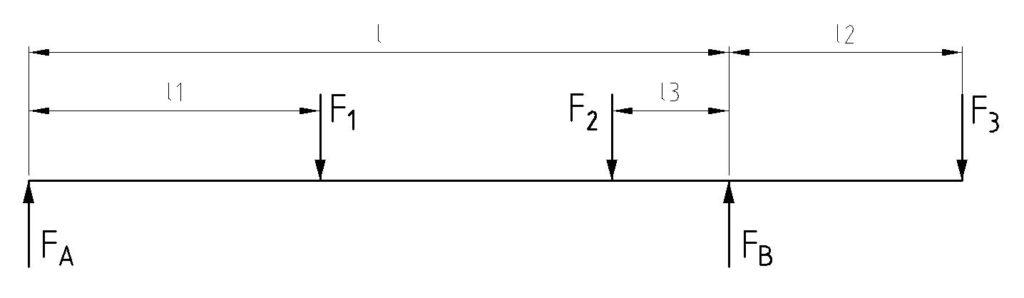
Zuerst berechnen wir die Stützkräfte.

$Σ M_{A} = 0 = - F_{1} \cdot l_{1} - F_{2} \cdot (l - l_{3}) + F_{B} \cdot l - F_{3} \cdot (l + l_{2}) F_{B} = \frac{F_{1} \cdot l_{1} + F_{2} \cdot (l - l_{3}) - F_{3} \cdot (l + l_{2})}{6} F_{B} = 45, 42 k N$ $Σ F_{Y} = 0 = F_{A} - F_{1} - F_{2} + F_{B} - F_{3} F_{A} = F_{1} + F_{2} + F_{3} - F_{B} F_{A} = 9, 583 k N$

Anschließend zeichnen wir den Querkraftverlauf. Bei diesem tragen wir z.B. von links nach rechts die Kräfte maßstäblich ein. Wichtig ist die Kraftvektoren nach oben zu zeichnen, wenn die Kraft positiv ist und sie nach unten zu zeichnen, wenn diese negativ ist. Von der ersten Kraft ausgehend ziehen wir rechtwinklig eine Linie, bis diese auf die nächste Kraft trifft. diese zeichnen wir wieder ihrer Kraftrichtung entsprechend ein. Und zwar ausgehend von dem Punkt an dem die rechtwinklige Linie auf die Kraftlinie traf. Dies machen wir bis wir alle Kräfte eingetragen haben.

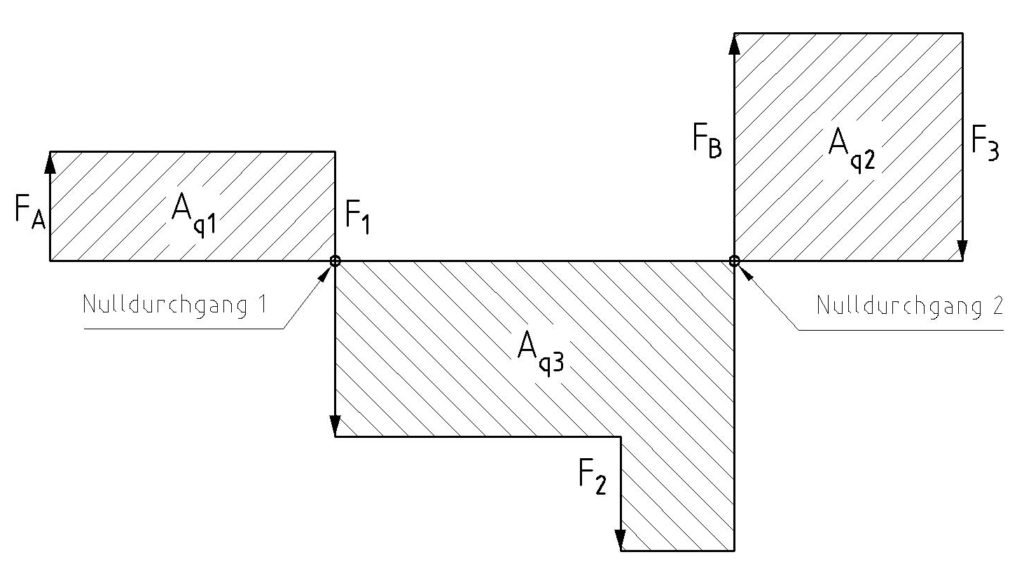
Vom Nulldurchgang ausgehend nach links oder nach rechts (je nachdem was schneller geht) ermitteln wir die Flächen links vom Nulldurchgang oder rechts vom Nulldurchgang. An dem Nulldurchgang an dem die Summe der ermittelten Flächen größer ist liegt das maximale Biegemoment an.

$M_{b 1} ≙ A_{q 1} = F_{A} \cdot l_{1} M_{b 1} = 23, 96 k N m M_{b 2} ≙ A_{q 2} = F_{3} \cdot l_{2} M_{b 2} = 40 k N m$

M_b2 ist größer als M_b1 dementsprechend liegt das maximale Biegemoment am Nulldurchgang 2 und beträgt 40 kNm.

Liegen neben einem Nulldurchgang mehrere Flächen an, so sind alle die über der Nulllinie liegen zu addieren und alle die darunter liegen davon zu subtrahieren.

Stützträger (Kragträger) mit Streckenlast

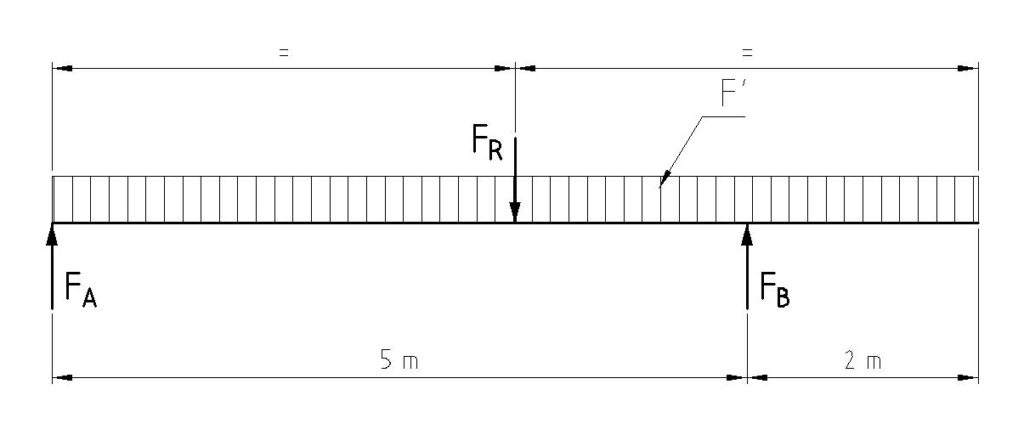
F‘ = 2000 N/m

Zunächst einmal müssen wir die resultierende Kraft F_R ermitteln.

$F_{R} = F ‚ \cdot l_{F ‚} F_{R} = 2000 \frac{N}{m} \cdot 7 m F_{R} = 14000 N$

Anschließend errechnen wir die Lagerkräfte.

$Σ M_{A} = 0 = - F_{R} \cdot 3, 5 m - F_{B} \cdot 5 m F_{B} = \frac{F_{R} \cdot 3, 5 m}{5 m} F_{B} = 9800 N$ $Σ F_{Y} = 0 = F_{A} - F_{R} + F_{B} F_{A} = F_{R} - F_{B} F_{A} = 4200 N$

Nun zeichnen wir wieder unseren Querkraftverlauf um das maximale Biegemoment zu ermitteln. Eine Besonderheit ist hier, dass wir nach 5 m die dort wirkende Last aus der Streckenlast nach unten gehen müssen. Nach 5 m beträgt diese 10000 N (5 m · 2000 N/m). Nach oben gehen wir dort jedoch wieder nur den Betrag der Kraft F_B.

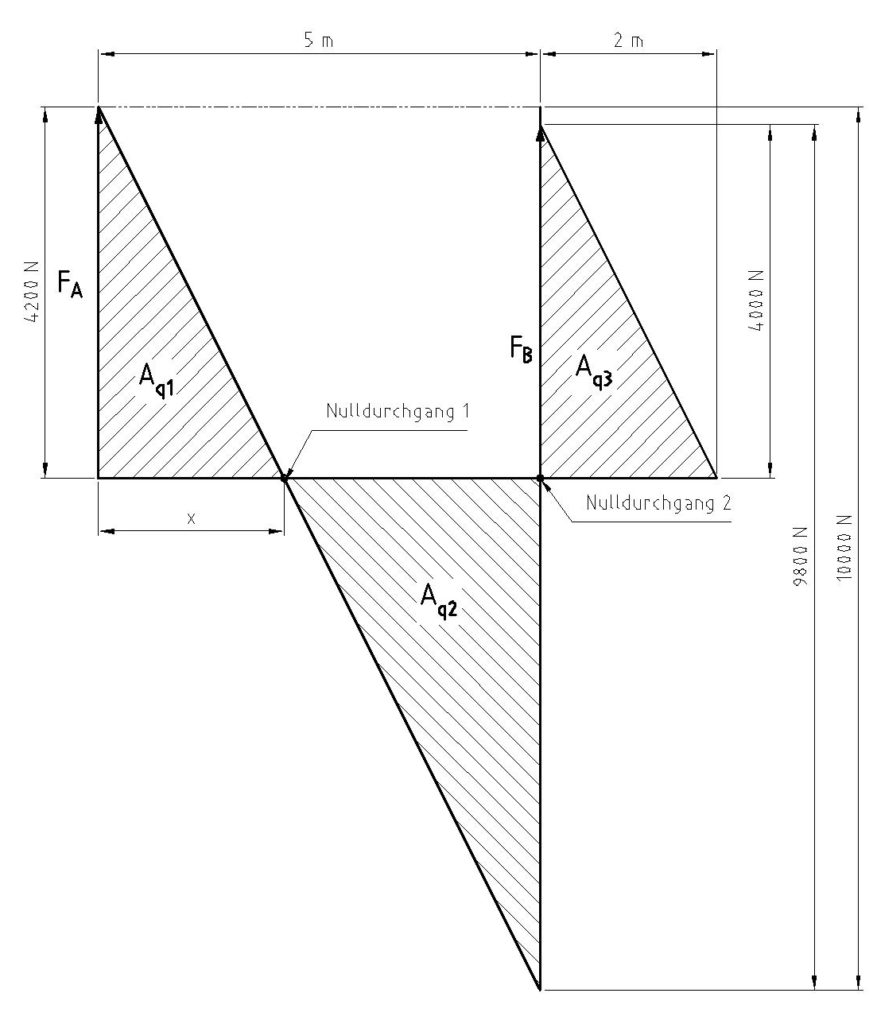
Zum ermitteln der Fläche A_q1 müssen wir eine lineare Gleichung aufstellen, da wir weder einen Winkel, noch die Strecke in der X-Achse kennen. Wir kennen jedoch die Steigung 2000 N/m. Das bedeutet ja, dass auf jeden Meter 2000 N kommen. Nun stellt sich die Frage nach wie vielen Metern beträgt die Kraft 4200 N.

$2000 \frac{N}{m} \cdot x = 4200 N | \div 2000 x = \frac{4200 N}{2000 \frac{N}{m}} x = 2, 1 m$

Nun können wir die Flächen ausrechnen.

$A_{q I} ≙ M_{b I} = \frac{F_{A} \cdot x}{2} = 4410 N m A_{q I I} ≙ M_{b I I} = \frac{F ‚ \cdot 2 m \cdot 2 m}{2} = 4000 N m M_{b I} > M_{b I I} \Rightarrow M_{b I} = M_{b m a x} = 4410 N m$ $4410 N m = 4410000 N m m$ $W_{e r f} = \frac{M_{b m a x}}{σ_{z u l}} W_{e r f} = \frac{4410000 N m m}{\frac{118 N}{m m ²}} W_{e r f} = 37373 m m ³ = 37, 37 c m ³$

In diesem Beispiel gehen wir von den 118 N/mm² aus. Hier würde ein IPE 240 benötigt werden.

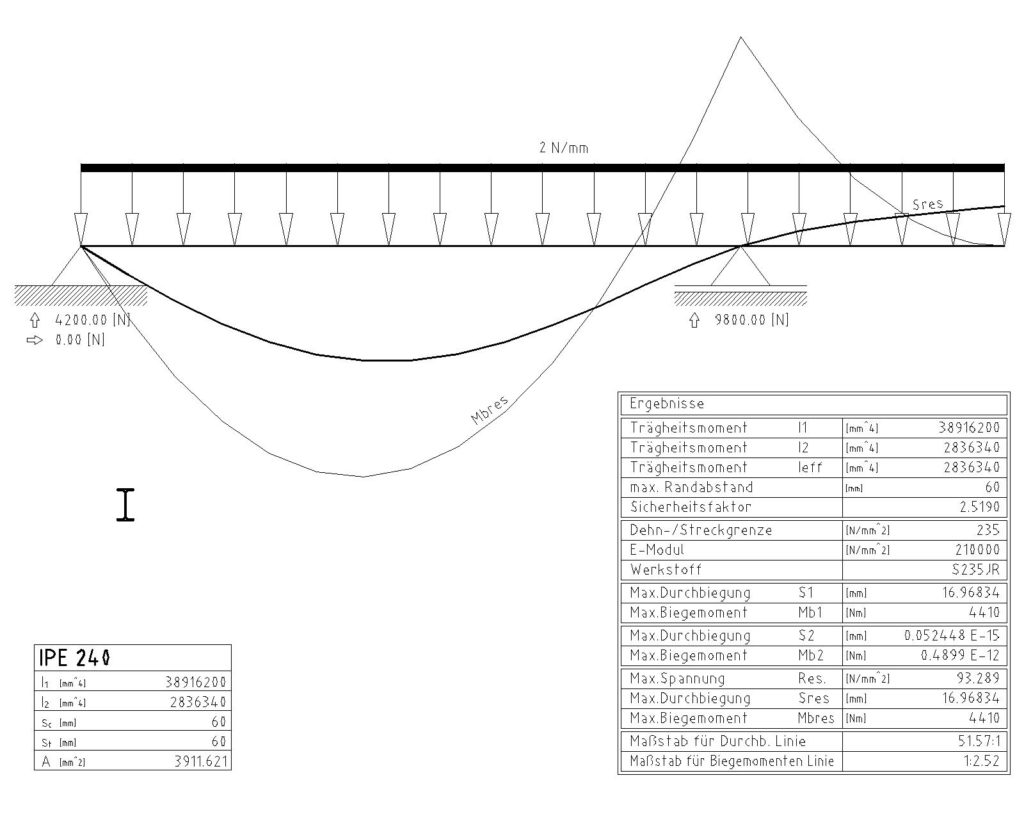
Eine Überprüfung in AutoCAD Mechanical bestätigt die Berechnung. Die maximale Durchbiegung beträgt 17 mm, was unter den zulässigen l/300 liegt.

Stützträger mit Mischlast

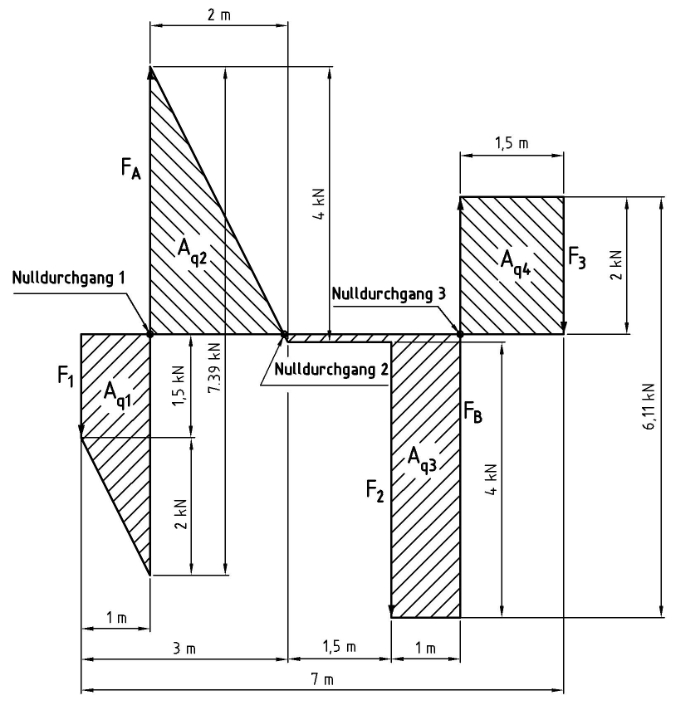
Freischneideskizze

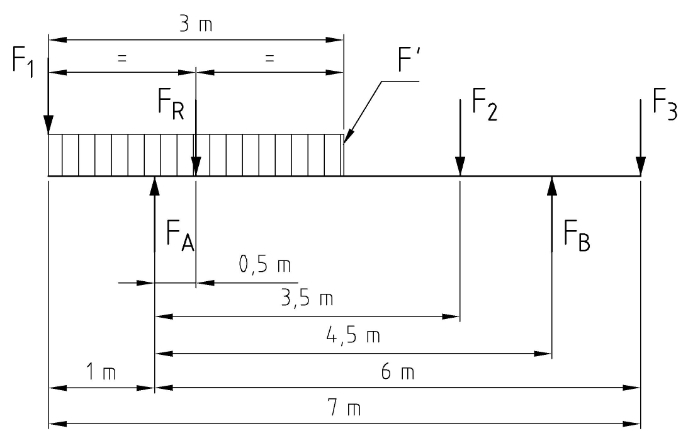
F₁= 1,5 kN
F₂ = 4 kN
F₃ = 2 kN
F‘ = 2 kN/m
F_R = 2 kN/m · 3 m = 6 kN

Unbekannte Kräfte ermitteln

$Σ M_{A} = 0 = F_{1} \cdot 1 - F_{R} \cdot 0, 5 - F_{2} \cdot 3, 5 + F_{B} \cdot 4, 5 - F_{3} \cdot 6 F_{B} = \frac{- F_{1} \cdot 1 + F_{R} \cdot 0, 5 + F_{2} \cdot 3, 5 + F_{3} \cdot 6}{4, 5} F_{B} = 6, 11 k N Σ F_{Y} = 0 = - F_{1} + F_{A} - F_{R} - F_{2} + F_{B} - F_{3} F_{A} = F_{1} + F_{R} + F_{2} - F_{B} + F_{3} F_{A} = 7, 388 k N$

Querkraftverlauf

Anschließend zeichnen wir den Querkraftverlauf. Zunächst gehen wir den Betrag der Kraft F1=1,5 kN nach unten. Wir wissen bereits, aus der Angabe der Streckenlast, dass die Kraft pro Meter 2 kN beträgt.

Nun gehen wir den Betrag der Kraft F_A nach oben und setzen den Verkauf der Streckenlast fort. 2 m bleiben noch übrig, also 4 kN.

Danach gehen wir 1,5 m horizontal bis zur Kraft F₂, die auch wieder vertikal nach unten zeigt. 1 m bis zu F_B die nach oben zeigt und letztlich 1,5 m nach F₃die nun wieder auf der Nulllinie auskommt.

Biegemomente

Jetzt errechnen wir die Flächen um zu ermitteln, wo unser maximales Biegemoment anliegt.

$A_{q 1} = 1, 5 k N \cdot 1 m + \frac{2 k N \cdot 1 m}{2} = 2, 5 k N m$

Bei der Fläche A_q2 müssen wir etwas genauer hinsehen, denn die Streckenlast reicht über den Nulldurchgang hinaus. Wir kennen aber die Höhe über dem Nulldurchgang nämlich: 7,388 kN – 1,5 kN – 2kN =3,88 kN und wir kennen ebenso die Steigung durch die Streckenlast, die 2 kN/m ist. Also die Vertikale ist doppelt so viel wie die Horizontale. Dies funktioniert mit jedem linearen Steigungsverhältnis, wenn auch weniger deutlich. Die Strecke bis zum Nullpunkt ist also 3,88 ÷ 2 = 1,945 m.

$A_{q 2} = \frac{1, 945 m \cdot 3, 88 k N}{2} = 3, 773 k N m$

Für A_q3 kann die selbe Erkenntnis genutzt werden. Auch wenn wir A_q3 maximal zur Kontrolle brauchen.

$A_{q 3} = 1 m \cdot (6, 11 k N - 2 k N) + 1, 5 m \cdot (6, 11 k N - 2 k N - 4 k N) + (2 m - 1, 945 m) \cdot (4 k N - 3, 773 k N) = 4, 29 k N m$

Und A_q4 ist sowieso simpel.

$A_{q 4} = 2 k N \cdot 1, 5 m = 3 k N m$

maximales Biegemoment

Das maximale Biegemoment liegt an dem Nullpunkt an, wo die Summe der Momente am größten ist. Dazu nehmen wir immer alle Flächen links oder rechts eines Nulldurchganges und addieren diese. Wobei nach unten zeigende Flächen negativ anzusehen sind. Bei den Ergebnissen ignorieren wir das negative Vorzeichen, da es keine negativen Kräfte gibt.

$M_{b I} ≙ A_{q 1} = - 2, 5 k N m \Rightarrow 2, 5 k N m M_{b I I} ≙ A_{q 2} - A_{q 1} = 1, 273 k N m M_{b I I I} ≙ A_{q 4} = 3 k N m M_{b m a x} = M_{b I I I} = 3 k N m$

erforderliches Widerstandsmoment

wir kennen nun das maximale Biegemoment. Fehlt uns nur noch die zulässige Biegespannung.

$σ_{b z u l} = \frac{σ_{b F}}{ν}$

Die Biegefließgrenze σ_bF beträgt bei Stahl ca. 1,2 · R_e also bei S235 ungefähr 282 N/mm² (In der Annahme, dass die Erzeugnisdicke < 16 mm ist). Der Sicherheitsfaktor ν gegen Fließen beträgt bei duktilen Werkstoffen ca. 1,5

$σ_{b z u l} = \frac{282 N}{m m ² \cdot 1, 5} = 188 N / m m ²$ $W_{e r f} = \frac{M_{b m a x}}{σ_{b z u l}} = \frac{3000000 N m m}{\frac{188 N}{m m ²}} = 15957, 45 m m ³$

Methode 2 – Schnittgrößen

Bei dieser Methode geht man grundsätzlich erst einmal genauso vor, dass die Gleichgewichtsbedingungen aufgestellt und die Lagerkräfte ermittelt werden.

Stützträger mit zwei Einzellasten

Länge = 12 m
F_St = 2200 N bei 4,5 m
F_V = 1700 N bei 1,7 m

Freikörperbild erstellen

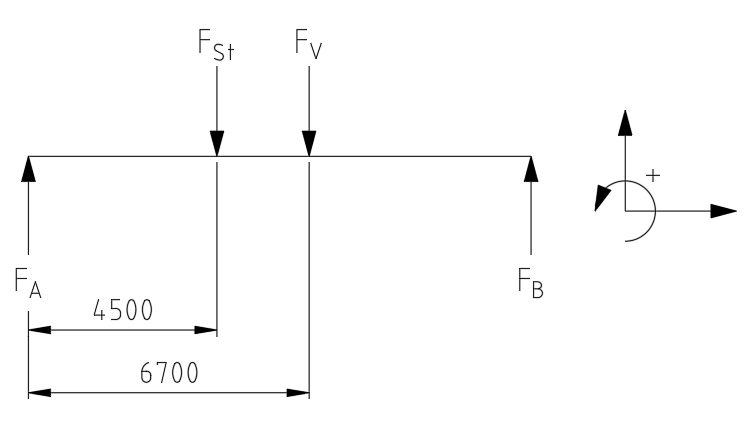
Gleichgewichtsbedingungen aufstellen

$\Sigma M_{A}=0=-F_{St}\cdot 4500\; mm-F_{V}\cdot 6700\; mm\;+\;F_{B}\cdot12000\;mm$

umstellen nach F_B

$F_{B}=\frac{F_{St}\cdot4500\;mm+FV\cdot6700\;mm}{12000\;mm}$

$F_{B}=1774,17\;N$

Wir können jetzt entweder noch ein Kräftegleichgewicht in Y Achse aufstellen, oder noch ein Momentengleichgewicht um den Punkt B.

$Σ M_{B} = 0 = F_{V} \cdot 5300 m m + F_{S t} \cdot 7500 m m - F_{A} \cdot 12000 m m u m s t e l l e n n a c h F_{A} F_{A} = \frac{F_{V} \cdot 5300 m m + F_{S t} \cdot 7500 m m}{12000 m m} F_{A} = 2125, 83 N$

Schnittgrößen ermitteln

In der zuvor gezeigten Methode würden wir nun den Querkraftverlauf zeichnen. Anstelle dessen ermitteln wir nun Schnittgrößen. Zu diesem Zweck teilen wir den Träger an der Stelle einer Kraft auf. Die beiden dadurch entstandenen Seiten des Trägers werden Schnittufer genannt.

Schnittpunkt 1

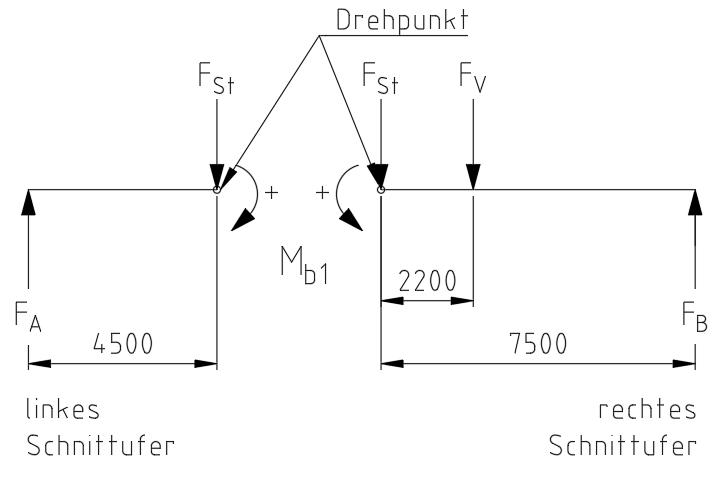
Jetzt legen wir den Schnittpunkt jeweils als neuen Drehpunkt für unsere Momentengleichung fest.

Dies hat nichts mehr mit dem Standard Koordinatensystem aus unserer Freischneideskizze zu tun!

Wir brauchen jedoch nur ein Schnittufer ausrechnen, je nachdem welches schneller geht. Die Summe aller Momente ist 0, sonst hätten wir kein statisches System, welches sich im Gleichgewicht befindet.

Wir legen weiterhin die positive Drehrichtung so fest, als würde der Träger an der geschnittenen Stelle nach unten fallen.

Das am Schnittpunkt anliegende Moment ist unser Biegemoment an dieser Stelle.

$M_{b 1} = F_{A} \cdot 4500 m m M_{b 1} = 9566, 24 N m$

Schnittpunkt 2

Das selbe Prinzip wenden wir nun bei der zweiten Schnittstelle an. (Es wird an jeder Kraft geschnitten, außer an den äußersten).

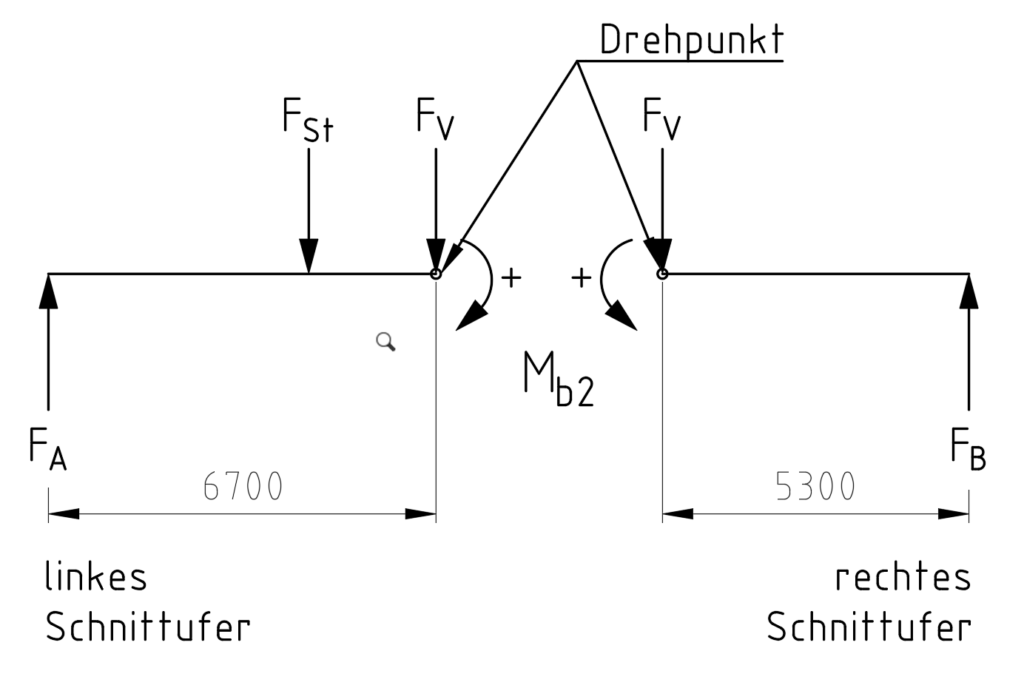
Würden wir hier die linke Seite wählen, so wären zwei Momente zu berechnen. M_A und M_St die Beträge müssten dann addiert werden.

Biegemomentenverlauf / Biegelinie

Um den Verlauf der Biegemomente zu visualisieren kann ein Biegemomentenverlauf gezeichnet werden. Dieser ist bei unserem Beispiel hier natürlich sehr übersichtlich.

Dazu tragen wir die X-Achse unsere Balkens ein und belegen die Y-Achse mit dem Wert der Biegemomente.

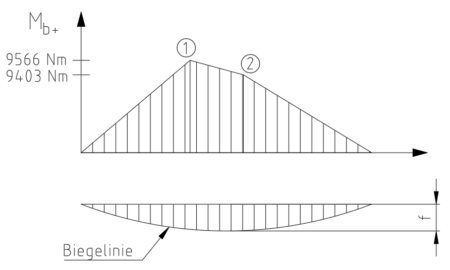
Unter dem Biegemomentenverlauf ist zusätzlich noch die Biegelinie eingezeichnet.

zulässige Biegespannung

Wir legen einen Sicherheitsfaktor v von 1,5 fest. Der Festigkeitskennwert ist die Streckgrenze R_eN. (Bei statischer Belastung)

Bei wechselnd/normaler Biegebelastung wäre das σ_bWN anstelle von R_eN

$σ_{b z u l} = \frac{σ_{b W N}}{ν}$

Beispiel Welle: Dreht sich eine Welle > 180° um die eigene Achse, so wirken die Kräfte wechselnd auf die Welle.

Bei schwellend/normaler Biegebelastung wäre das σ_bSchN

$σ_{b z u l} = \frac{σ_{b S c h N}}{ν}$

Beispiel Welle: Dreht sich eine Welle < 180° um die eigene Achse, so wirken die Kräfte wechselnd auf die Welle.

$σ_{b z u l} = \frac{R_{e N}}{ν} σ_{b z u l} = \frac{235 N}{m m^{2} \cdot 1, 5} σ_{b z u l} = 156, 67 N / m m ²$

Dimensionierung

Jetzt kommen wir zu dem Teil, warum wir das Ganze überhaupt machen. Wir wollen wissen, welchen Träger wir benötigen. In unserem Beispiel soll es aus konstruktiven Gründen ein flach liegendes U-Profil sein.

Erforderliches Widerstandsmoment

$W_{b e r f} = \frac{M_{b m a x}}{σ_{b z u l}} = \frac{9566240 N m m \cdot m m ²}{156, 67 N} W_{b e r f} = 61, 059, 81 m m ³ \Rightarrow 61, 06 c m ³$

Ein flach liegendes U-Profil wird um die Y-Achse gebogen.

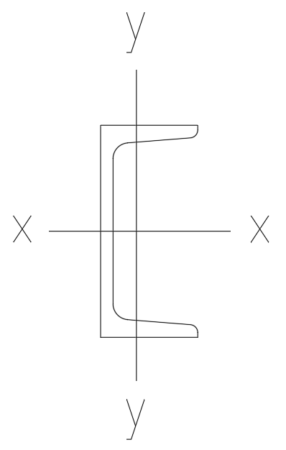
Dies entspricht dem Wert W_yim Roloff Matek Tabellenbuch. Wir würden also einen U 300 benötigen.

vorhandene Sicherheit

Zum Schluss schauen wir noch, ob wir die geforderte Sicherheit von 1,5 eingehalten haben. Dafür benötigen wir zuvor noch die vorhandene Biegespannung σ_bvorh.

$σ_{b v o r h} = \frac{M_{b m a x}}{W_{b v o r h}} = \frac{9566240 N m m}{67800 m m ³} σ_{b v o r h} = 141, 09 N / m m ² ν_{v o r h} = \frac{σ_{b}}{σ_{b v o r h}} \Rightarrow \frac{R_{e N}}{σ_{b v o r h}} = \frac{235 N \cdot m m ²}{m m ² \cdot 141, 09 N} ν_{v o r h} = 1, 67 \Rightarrow a u s r e i c h e n d!$

5 Kommentare

André
17. Oktober 2023 / 14:11 Antworten
Hallo Nils, es ist sehr gut so eine Darstellung/Erklärung ca. 35 Jahre nach dem Studium zu finden. Da ploppt doch Verschollenes wieder an die Oberfläche! Mir hat es sehr geholfen wieder in die Materie reinzukommen um das max. Biegemoment bei unsymmetrisch wirkenden Einzellasten zu definieren.
Glückwunsch, sehr gelungen und ein riesen großes Dankeschön!!!
Walter Gombert
21. September 2023 / 10:11 Antworten
Beim Freikörperbild ist nach meiner Meinung ein Vorzeichenfehler. Aufgrund der Definition muss es daher heißen;
Summe MA=0= -Fst*4500mm-Fv*6700 mm + FB*12000mm
(Habe alles geschrieben in Buchstaben, die Sonderzeichenkriege ich hier nicht hin) Hoffe, das ist trotzdem verständlich!
- Nils
  6. Oktober 2023 / 16:56 Antworten
  Vielen Dank für den Hinweis, der natürlich vollkommen korrekt ist. Habe ich korrigiert.
Ersin
15. Februar 2023 / 0:45 Antworten
Hi, super Seite.
Eine Frage: in dem Beispiel „Stützträger (Kragträger) mit mehreren Einzellasten“ werden jeweils Aq1 und Aq2 berechnet, aber nicht Aq3, dabei ist Aq3 mit 64kNm deutlich größer.
Gibt es dafür einen Grund?
- Nils
  15. Februar 2023 / 7:26 Antworten
  Hallo Ersin,
  vielen Dank für das Lob. Ja es gibt dafür einen Grund. Um das Biegemoment am Nulldurchgang zu ermitteln kann man entweder von links oder rechts alle Momente ermitteln, die bis zum Nulldurchgang auftreten. Da es hier der schnellste Weg war AQ1 und AQ2 zu ermitteln, habe ich das auch getan. Du wirst feststellen, dass es auch keinen Unterschied macht. Wenn du AQ3 von AQ1 abziehst kommst du ebenfalls auf 40 kNm. Schau dir am besten auch das Beispiel: „Stützträger mit Mischlast“ an. Da wird es deutlicher. Ich hoffe ich konnte helfen.