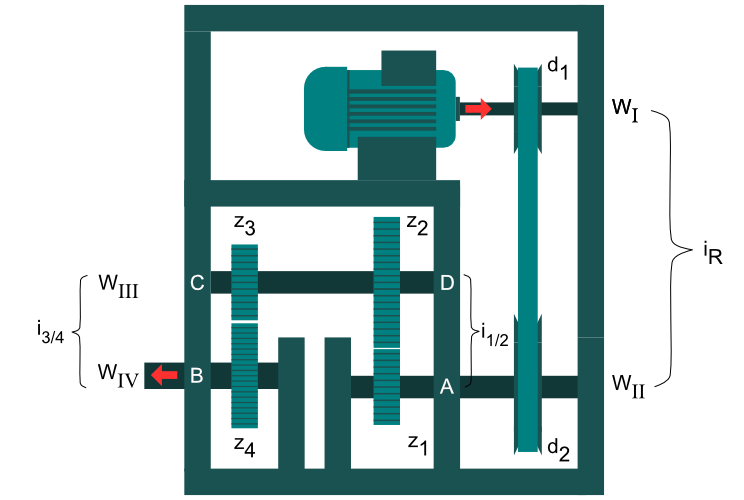
In diesem Beispiel für die Berechnung von Getrieben wird ein Riementrieb von einem Elektromotor angetrieben. Der Riementrieb treibt wiederum ein zweistufiges Zahnradgetriebe an. Die Vorgehensweise basiert dabei auf dem Roloff Matek.
Der Propeller eines Industriegebläses soll mit einem Elektromotor angetrieben werden. Zu ermitteln sind:
- Die Leistung und Auswahl eines geeigneten Elektromotors
- Auswahl und Berechnung des Riementriebs
- Berechnung des Zahnradgetriebes
- Dimensionierung der Zwischenwelle am Zahnrad 2 und 3 mit dynamischen Festigkeitsnachweis
Weiter sind folgende Randbedingungen zu erfüllen:
- Betriebstemperatur < 55°C
- Propellerdrehzahlen sollen möglichst genau erreicht werden.
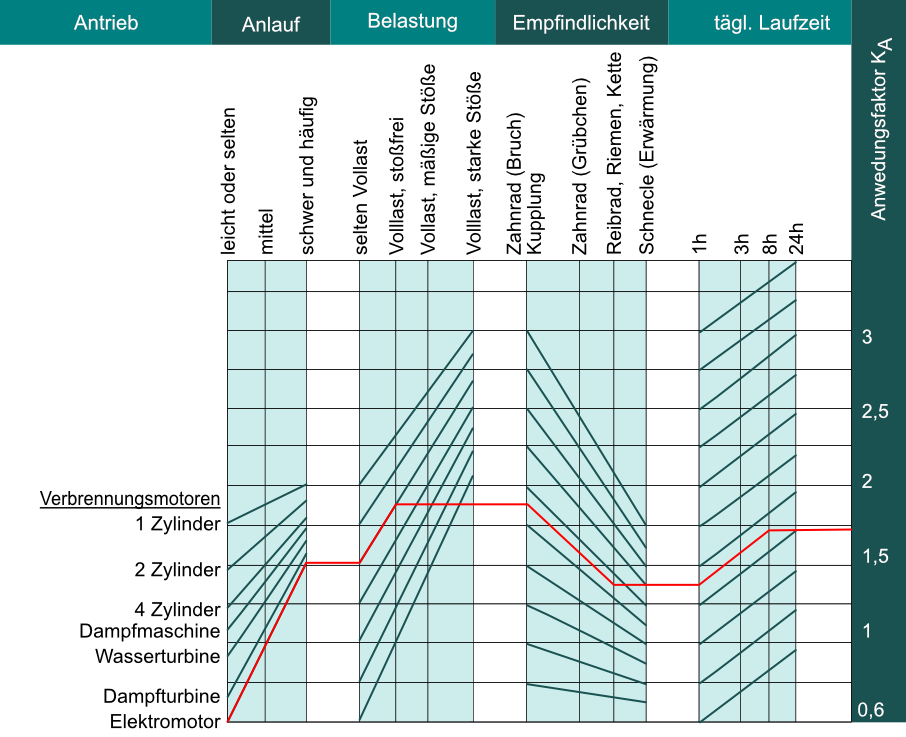
- Der Antrieb soll für eine tägliche Nutzungsdauer von 8 h, häufiger Anlauf, Volllast stoßfrei ausgelegt werden.
- Die Bauelemente müssen dauerhaft chemischen Korrosionseinflüssen widerstehen können.
- Es sollen möglichst genormte Bauteile zum Einsatz kommen.
- Die Propellerdrehzahl soll 750 min-1 betragen.
- Das Antriebsmoment am Propeller beträgt 70 Nm.
- Es soll ein Motor mit 3000 min-1 eingesetzt werden.
Riementrieb
- Die maximalen Scheibengrößen dürfen platzbedingt nicht mehr als 250 mm betragen.
- Die Zielübersetzung beträgt 1,3
- Wirkungsgrad 82 %
- geplanter Wellenabstand 350 mm
Zahnradgetriebe
- zwei Getriebestufen
- platzsparend (Antriebs- und Abtriebswelle ungefähr auf gleicher Höhe)
- Zwischenwelle oberhalb Antriebs- Abtriebswelle
- Wirkungsgrad 90 %
- gerade verzahnte Stirnräder im Pressverband aufgeschrumpft
- Übersetzung i1/2 = 1,9
- Zahnrad 1 z = 20, m = 4 mm
- Zahnrad 3 z = 20, m = 4 mm
- Mittenabstand zwischen den Zahnrädern = 200 mm
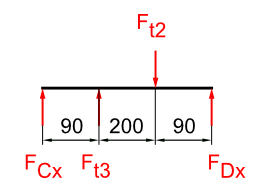
- Mittenabstand zu den Gehäuselagern = 90 mm
- Wellenwerkstoffe; X2CrNiN23-4
Berechnung von Getrieben (Motordimensionierung)
Nettoleistung
PNetto = 5,5 kW
Anwendungsfaktor KA
KA = 1,75
Bruttoleistung
Motorauswahl
Gewählter Motor 160L-18,5-3000 [16-21]
Berechnung von Getrieben (Riementrieb)
Riementyp- profil
gewählter Riementyp: Schmalkeilriemen (raumsparend)
gewähltes Riemenprofil: SPZ (keine größeren Riemenscheiben zu erwarten)
Scheibendurchmesser
Die erste Riemenscheibe dimensionieren wir anhand der maximal zulässigen Wellenbelastung anhand [TB 16-21]. Werte für Motoren mit 1500 min-1 gibt es nicht. Wir können die Werte aber dennoch annehmen, da mit zunehmender Kraft die Motorenhersteller auch größere Wellen verbauen werden.
Die Gleichung stellen wir nach d um.
Anhand des geplanten Wellenabstandes von 350 mm sehen wir, dass keine Kollision der Riemenscheiben stattfinden wird, wenn wir die Radien addieren.
vorläufiger Wellenabstand
Der vorläufige Wellenabstand kann wie geplant 350 mm betragen.
Riemenlänge
Wellenabstand
Anzahl der Keilriemen
PN=5,5 kW [16-15b]
ÜZ=0,3 [16-16b]
c1=0,98 [16-17a]
c2=0,91 [16-17c]
Berechnung von Getrieben (Zahnradgetriebe)
Getriebeplan
Getriebedaten
Für die Berechnung von Getrieben müssen die Getriebestufen definiert sein.
1. Stufe
zuerst übernehmen wir die bekannten Daten.
z1 = 20 Zähne, m = 4 mm, i1/2= 1,9
Die unbekannten Daten können wir errechnen.
die tatsächlichen Übersetzungsverhältnisse sind wichtig, um die korrekten Drehzahlen bestimmen zu können.
2. Stufe
z3 = 20 Zähne, m = 4 mm
Für die zweite Getriebestufe ist kein Übersetzungsverhältnis gegeben. Dieses können wir uns jedoch anhand der Gesamtübersetzung errechnen.
Das Gesamtübersetzungsverhältnis ist das Produkt der einzelnen Übersetzungsverhältnisse.
Dieses können wir nun nach i3/4 umstellen.
Nun können wir die fehlenden Daten berechnen.
Auch hier ermitteln wir wieder das tatsächliche Übersetzungsverhältnis.
Durchmesser
Drehmomente
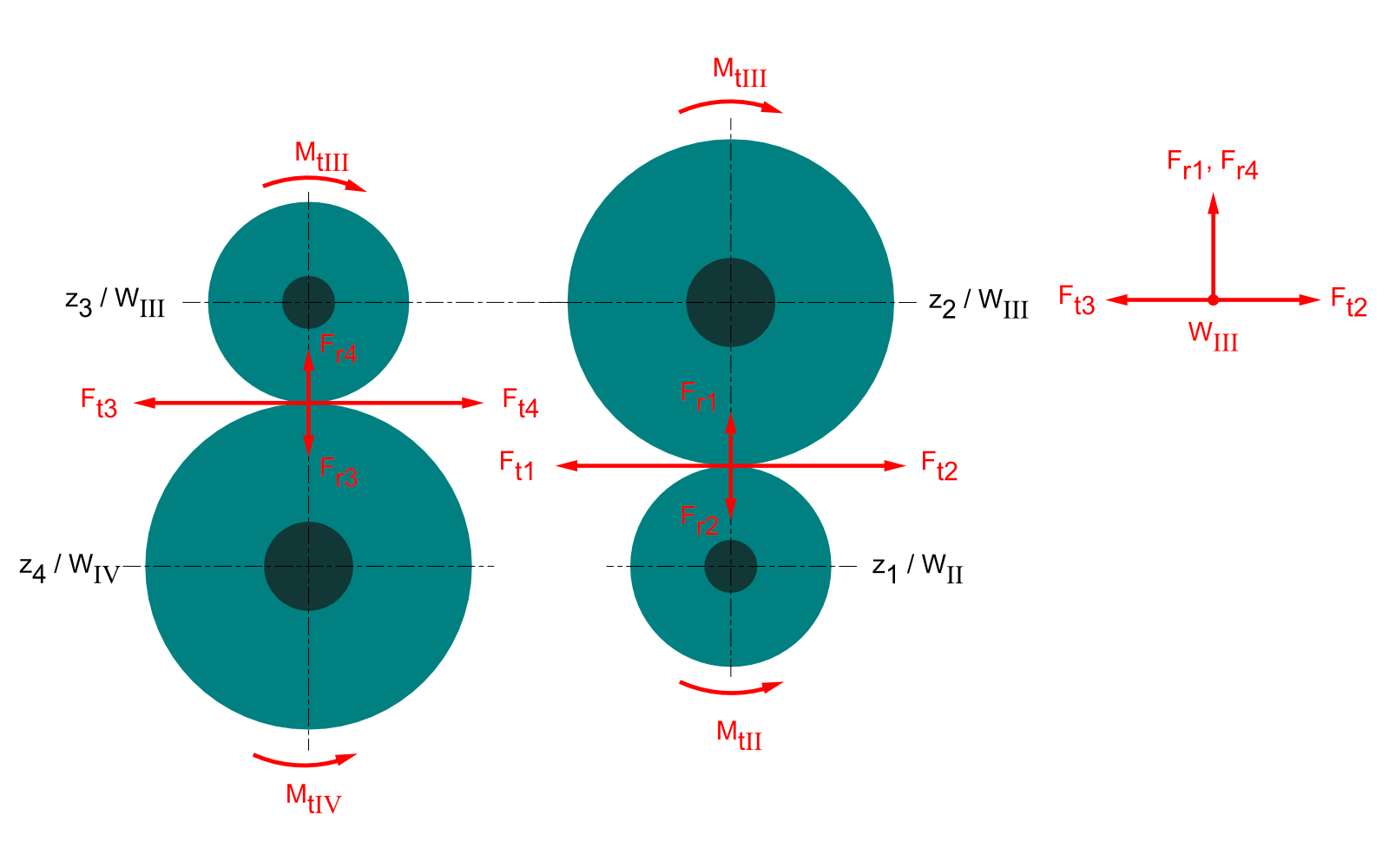
Tangential- Radialkräfte
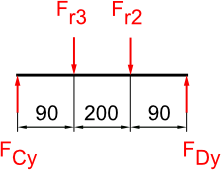
Stütz- Lagerkräfte
X-Horizontal
Y-vertikal
resultierende Kräfte
Biege- Vergleichsmomente

Gestaltwechselfestigkeit
Stelle 1
Zunächst müssen wir zum Ablesen einiger Faktoren den überschlägigen Durchmesser ermitteln.
Jetzt können wir aus den Tabellen die benötigten Werte ablesen.
σbWN = 300 N/mm² [1-1] Kt = 1 [3-11] SDerf = 1,8 [3-14a/c] βKb ≈ 2,3 [3-8] Kg = 0,92 [3-11] KOσ = 0,92 [3-10] KV = 1 [3-12]
Stelle 2
Die gleiche Vorgehensweise können wir bei Stelle 2 anwenden.
σbWN = 300 N/mm² [1-1] Kt = 1 [3-11] SDerf = 1,8 [3-14a/c] βKb ≈ 2,3 [3-8] Kg = 0,9 [3-11] KOσ = 0,92 [3-10] KV = 1 [3-12]
Durchmesser
Bei der Berechnung von Getrieben ist die richtige Dimensionierung der Wellen ein maßgebender Faktor. Nun können wir diese Dimensionierung vornehmen, da uns alle Einflussgrößen bekannt sind.