Zentrales Kräftesystem

Eine Kräftegruppe wird als zentrales ebenes Kräftesystem bezeichnet wenn alle Kräfte auf einer Ebene liegen und alle Wirkungslinien sich in einem Punkt schneiden.

Der Parallelogrammsatz ermöglicht es uns „gerichtete Vektoren“ (Geschwindigkeiten ν, Beschleunigungen a, Wegen s und Kräfte F) zusammenzusetzen oder zu zerlegen.

Zusammensetzen von zwei nicht parallelen Kräften (Kräftereduktion)

Kräfte sind linienflüchtige Vektoren, dass bedeutet, dass sie auf ihrer Wirklinie beliebig verschoben werden dürfen. Wir können also zwei nicht parallel wirkende Kräfte auf einen gemeinsamen zentralen Punkt verschieben. Diesen Schritt nennen wir eine geometrische Addition. Das Verfahren wird als Kräftereduktion bezeichnet.

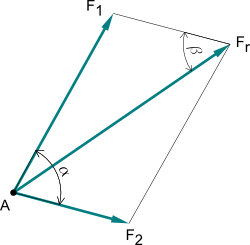
Es gelten folgende Beziehungen:

Die Dreiecke die hier entstehen sind selten rechtwinklig (Dies wäre Zufall).
Die Strecke [AF₂] ist parallel zur Strecke [F₁F_r].
Die Strecke [AF₁] ist parallel zur Strecke [F₂F_r].
Der Winkel α lässt sich ebenso auf die andere Seite „spiegeln“.
Wie in jedem anderen Parallelogramm ergeben zwei benachbarte Winkel zusammen immer 180°.

Die Kräfte F₁ und F₂werden geometrisch zu F_r (Resultierende Kraft) addiert.

$F_{r} = \sqrt{{F_{1}}^{2} + {F_{2}}^{2} + 2 \cdot F_{1} \cdot F_{2} \cdot \cos (α)}$ $β = a r c \sin (\frac{F_{1} \cdot \sin (α)}{F_{r}})$

Parallelogrammsatz
Die Resultierende F_r (Ersatzkraft) zweier an einem Punkt angreifender Kräfte F₁ und F₂ ist die Diagonale des Parallelogramms.

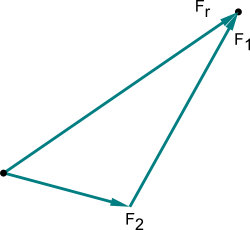
Krafteck

Das oben dargestellte Kräfteparallelogramm kann auch als Dreieck dargestellt werden. Der Sinn bleibt der Gleiche.

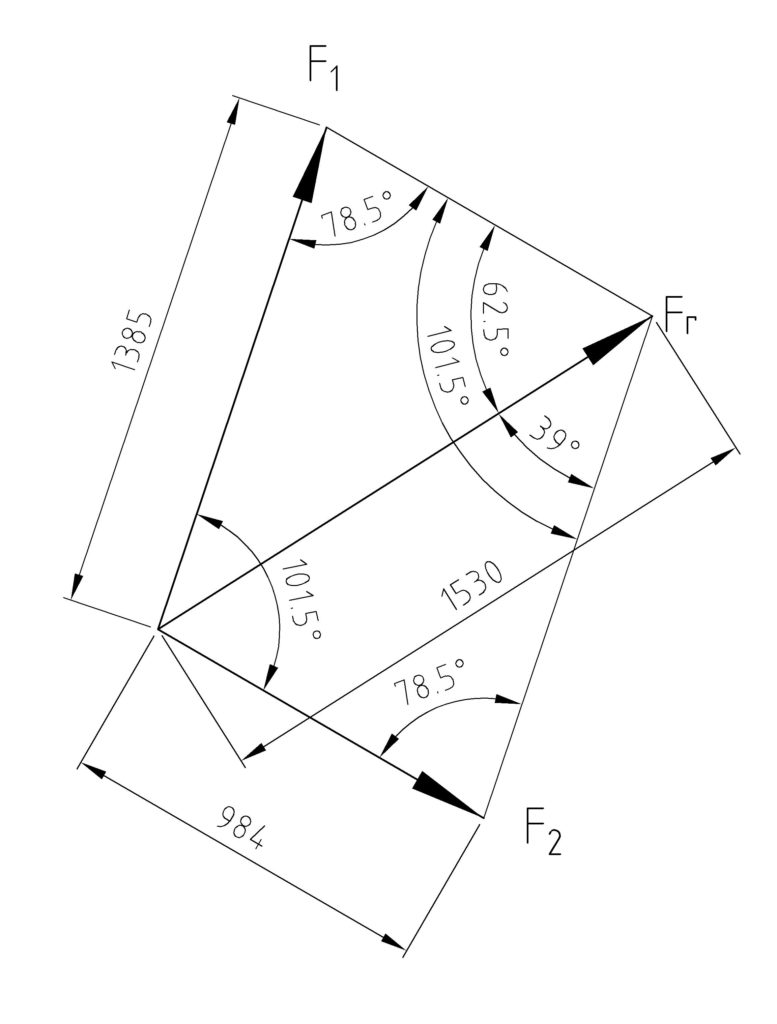
Beispiel

$F_{r} = \sqrt{(1385 N)^{2} + (984 N)^{2} + 2 \cdot 1385 N \cdot 984 N \cdot \cos (101, 5 °)} F_{r} = 1530 N$ Diese Formel funktioniert natürlich auch bei Rechtecken, also wenn Kräfte rechtwinklig zueinander stehen. Da wäre der Winkel α logischerweise 90°. Natürlich kann in diesem Fall auch der Tangens bzw. Arcustangens verwendet werden.

$β = a r c \sin (\frac{1385 N \cdot \sin (101, 5 °)}{1530 N}) β = 62, 5 °$

Berechnen

Zerlegen einer Kraft in zwei nicht parallele Kräfte

Ist die resultierende Kraft F_rgegeben und werden stattdessen die Einzelkräfte F₁ und F₂ gesucht, kann das Kräfteparallelogramm anhand der resultierenden Kraft und der Wirklinien der Einzelkräfte gezeichnet werden.

Dazu werden die Wirklinien parallel auf den Endpunkt der resultierenden Kraft versetzt. Die Punkte an denen sich diese schneiden sind dann die Endpunkte der Einzelkräfte.

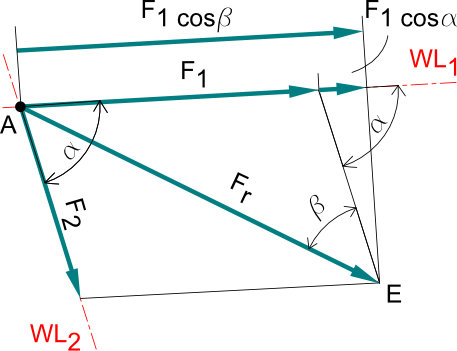
Wir können nun diese Kräfte auch berechnen.

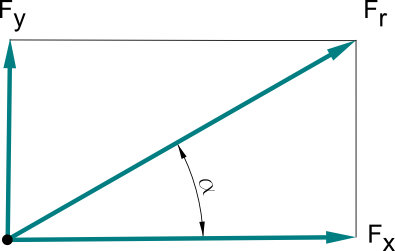
$F_{2} = F_{r} \cdot \frac{\sin (β)}{\sin (180 ° - α)}$ $F_{1} = F_{r} \cdot \cos (β) - F_{2} \cdot \cos (α)$

Resultierende Kraft aus rechtwinkligen Einzelkräften

Oft ist es nötig die resultierende Kraft F_r in zwei Einzelkomponenten F_x und F_y zerlegen. Dazu wird die resultierende Kraft unter dem Winkel α in ein Koordinatensystem eingezeichnet. Die Einzelkräfte können dann anhand der Winkelfunktionen Sinus und Cosinus errechnet werden.

$F_{x} = F_{r} \cdot \cos (α)$
$F_{y} = F_{r} \cdot \sin (α)$

Schreibe einen Kommentar