Berechnung von Zahnradgetrieben

Bei der Berechnung von Zahnradgetrieben sollte man mit der grundsätzlichen Geometrie von Zahnrädern vertraut sein. Auch die Grundlagen von Zahnradgetrieben sind hilfreich.

Formelzeichen – Berechnung von Zahnradgetrieben

Formelzeichen	Bezeichnung	Einheit
P	Leistung	kW, W, Nm/s
z	Anzahl der Zähne	–
i	Übersetzungsverhältnis	–
m	Modul	–
M	Drehmoment	Nm
M_b	Biegemoment	Nm
M_V	Vergleichsmoment	Nm
d	Teilkreisdurchmesser	mm
F_t	Tangentialkraft / Umfangskraft	N
F_r	Radialkraft	N
σ_{b zul}	zulässige Biegespannung	N/mm²

Formeln

Drehmoment

$M=F\cdot r=\frac{P}{2\cdot\pi\cdot n}$

Tangentialkraft / Umfangskraft

$F=\frac{P}{\nu}=\frac{P}{\pi \cdot d \cdot n}=\frac{M}{r}$

Teilkreisdurchmesser

$d=m\cdot z$

Übersetzung

$i=\frac{\omega _{1}}{\omega _{2}}=\frac{n _{1}}{n _{2}}=\frac{d _{2}}{d _{1}}=\frac{z _{2}}{z _{1}}$

Beispiel 1 – zweistufiges Stirnradgetriebe

Dieses Beispiel wird auch im Böge Aufgabenbuch behandelt. Das zweistufige Stirnradgetriebe hat 4 geradverzahnte Zahnräder und wird mit einem Elektromotor angetrieben, der eine Ausgangsleistung von 4 kW bei 960 min^-1aufweist. Folgende Werte sind bekannt:

z₁ = 19, z₃ = 25, i₁ = 3,2, i₂ = 2,8, m_1/2 = 6 mm, m_3/4= 8 mm, Eingriffswinkel α = 20°

Gesucht sind folgende Werte:

Drehmoment M₁
Teilkreisdurchmesser d₁
Zähnezahl z₂
Tangentialkraft F_T1
Radialkraft F_R1
Lagerkräfte F_A und F_B
maximales Biegemoment M_{bI max}
Vergleichsmoment M_V1
erforderlicher Wellendurchmesser d_I (σ_bzul = 50 N/mm²)
Drehmoment M_II
Teilkreisdurchmesser d₂, d₃
Zähnezahl z₄, Teilkreisdurchmesser d₄
Tangentialkraft F_T3, Radialkraft F_R3
Lagerkräfte F_C und F_D
maximales Biegemoment M_{bII max}
Vergleichsmoment M_VII
Wellendurchmesser d_II (σ_bzul= 50 N/mm²)

1 Drehmoment M₁

Das Drehmoment können wir anhand der Leistung und der Umfangsgeschwindigkeit ermitteln.

$F=\frac{P}{v}=\frac{P}{\pi\cdot d \cdot n}$ [F 16-41]

zunächst stellen wir Gleichung nach P um

$F=\frac{P}{\pi\cdot d \cdot n} \;|\cdot\pi\cdot d\cdot n$

$P=F\cdot \pi \cdot d\cdot n$

Für d setzen wir 2r ein, da das Drehmoment Kraft · Länge des Hebelarms ist und dieser ist bei zylinderförmigen Bauteilen der Radius.

$P=F\cdot \pi \cdot 2\cdot r\cdot n$

Wir finden nun in der Gleichung die Formel für das Drehmoment M=F·r wieder und können es einsetzen. F und r fallen also raus und M wird eingesetzt.

$P={\color{DarkGreen} M}\cdot\cancel{{\color{DarkRed} F}}\cdot \pi \cdot 2\cdot \cancel{{\color{DarkRed} r}}\cdot n$

und nochmal in schön.

$P=M\cdot\pi \cdot 2\cdot n$

Diese Gleichung können wir nun nach M umstellen.

$P=M\cdot\pi \cdot 2\cdot n \;|\div(\pi\cdot 2\cdot n)$

$M_{1}=\frac{P}{2\cdot \pi\cdot n_{1}}$

Nun können wir einsetzen.

$M_{1}=\frac{4000 \;Nm\cdot 60\;s}{s\cdot 2\cdot \pi\cdot 960}= \underline{\underline{39,79 \;Nm}}$

2 Teilkreisdurchmesser d₁

Der Teilkreisdurchmesser ist das Produkt aus Zähnezahl und Modul

$d_{1}=m_{1/2}\cdot z_{1}$

$d_{1}=6 \;mm\cdot 19=\underline{\underline{114\;mm}}$

3 Zähnezahl z₂

z₂ können wir anhand von z₁ und dem Übersetzungsverhältnis i₁ ermitteln

$i=\frac{z_{2}}{z_{1}}\;|\cdot z_{1}$

$z_{2}=i\cdot z_{1}$

$z_{2}=3,2\cdot 19=\underline{60,8}$

Wir wählen nach [TB 1-16] den nächstliegenden Wert, um das Übersetzungsverhältnis so wenig wie möglich zu verfälschen. Wir beachten dabei auch die Grenzzähnezahl von 17 [F 21-16]. Liegen aber weit darüber.

$z_{2gew}=\underline{\underline{60}}$

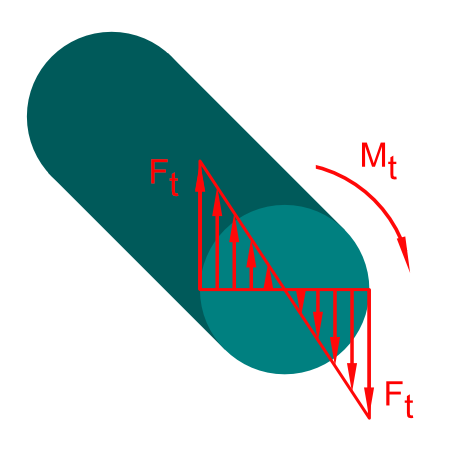
4 Tangentialkraft F_T1

Die Tangentialkraft ist die Umfangskraft an der Welle also der Quotient aus Drehmoment und dem Radius.

$F_{t1}=\frac{M_{1}}{r_{1}}$

$r_{1}=\frac{d_{1}}{2}=\frac{114\;mm}{2}=57\;mm$

$F_{t1}=\frac{39,79 \;Nm}{57\cdot 10^{-3\;}\;m}=\underline{\underline{698,07\;N}}$

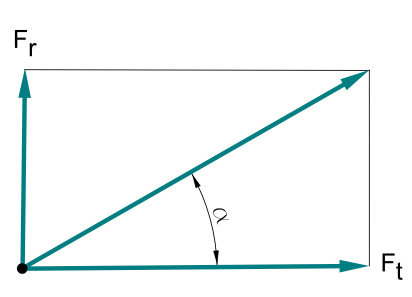
5 Radialkraft F_r₁

Aufgrund der Zahnflankenform ergibt sich am Zahn ein Eingriffswinkel α von 20° durch diese „Schrägstellung“ wird die Tangentilakraft teilweise in eine Radialkraft aufgeteilt. Dies bedeutet aber auch, dass an der Welle ein zweiachsiger Spannungszustand herrscht.

$F_{r}=tan(\alpha)\cdot F_{t}$

$F_{r}=tan(20\degree)\cdot 698,07 N =\underline{\underline{254,08\;N}}$

6. Lagerkräfte F_A und F_B

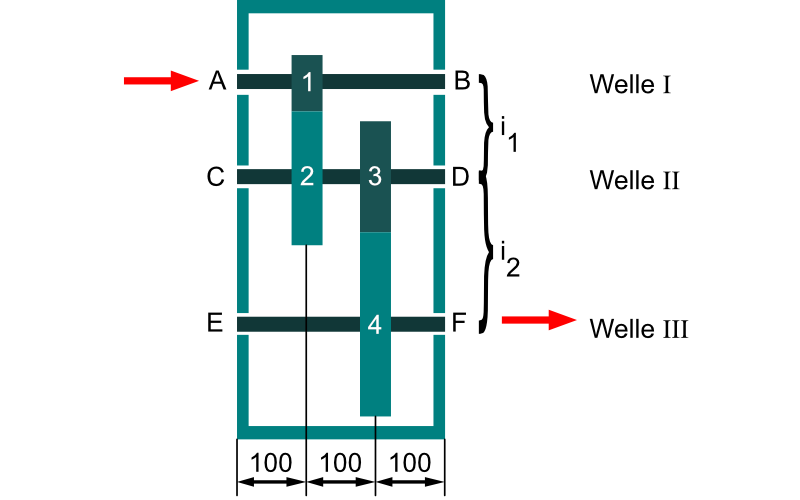
Wie bereits erwähnt herrscht nun an der Welle ein zweiachsiger Spannungszustand, um dies zu visualisieren, gibt es mehrere Möglichkeiten. Man kann sich einen zweidimensionalen Getriebeplan aufzeichnen und dann die Welle einmal vertikal und einmal horizontal freischneiden. Oder man zeichnet die Welle perspektivisch auf. Die Rechnung bleibt die Gleiche.

Dimetrische Darstellung

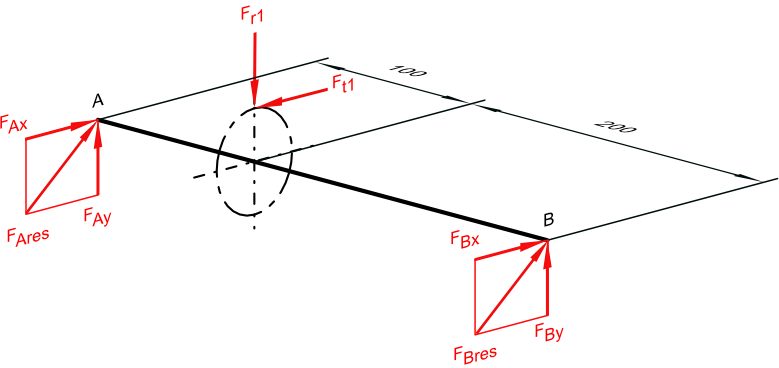
Getriebeplan

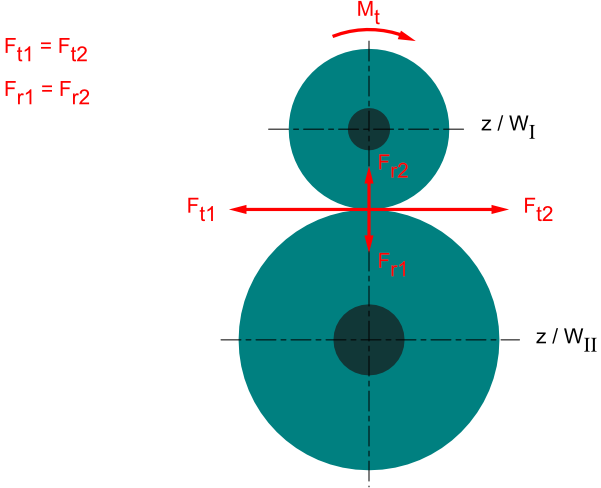
In welcher Richtung man das Drehmoment annimmt spielt keine Rolle. Nur die Indizes der Tangential- und Radialkräfte sollte dazu passen.

Freikörperbild Welle 1 vertikal

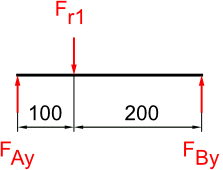
Nun können wir die Lagerkräfte berechnen. Wie das genau geht, habe ich im verlinkten Beitrag schon beschrieben.

$\circlearrowleft\Sigma M_{Ay}=0=-F_{r1}\cdot 100\;mm\;+\;F_{By}\cdot 300\;mm$

$F_{By}=\frac{F_{r1}\cdot 100\;mm}{300\;mm}=\frac{254,08\;N\cdot 100\;mm}{300\;mm}$

$F_{By}=84,69\;N$

$\circlearrowleft\Sigma M_{By}=0=F_{r1}\cdot 200\;mm\;+\;-F_{Ay}\cdot 300\;mm$

$F_{Ay}=\frac{F_{r1}\cdot 200\;mm}{300\;mm}=\frac{254,08\;N\cdot 200\;mm}{300\;mm}$

$F_{Ay}=169,39\;N$

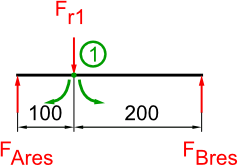
Freikörperbild Welle 1 horizontal

$\circlearrowleft\Sigma M_{Ax}=0=-F_{t1}\cdot 100\;mm\;+\;F_{Bx}\cdot 300\;mm$

$F_{Bx}=\frac{F_{t1}\cdot 100\;mm}{300\;mm}=\frac{698,07\;N\cdot 100\;mm}{300\;mm}$

$F_{Bx}=232,69\;N$

$\circlearrowleft\Sigma M_{Bx}=0=F_{t1}\cdot 200\;mm\;+\;-F_{Ax}\cdot 300\;mm$

$F_{Ax}=\frac{F_{t1}\cdot 200\;mm}{300\;mm}=\frac{698,07\;N\cdot 200\;mm}{300\;mm}$

$F_{Ax}=465,38\;N$

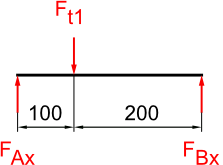
resultierende Kräfte

$F_{Ares}=\sqrt{F_{Ax}\;^2+F_{Ay}\;^2}$

$F_{Ares}=\sqrt{\left (465,38\;N\right )^2+(169,39\;N)^2}$

$F_{Ares}=495,25\;N$

$F_{Bres}=\sqrt{F_{Bx}\;^2+F_{By}\;^2}$

$F_{Bres}=\sqrt{\left (232,69\;N\right )^2+(84,69\;N)^2}$

$F_{Bres}=247,62\;N$

7. maximales Biegemoment Welle I

Nun können wir mit den resultierenden Lagerkräften das maximale Biegemoment ermitteln. Dafür betrachten wir nur die Tangentialkräfte und die Lagerkräfte. Die Radialkräfte berücksichtigen wir bei der Torsion.

$M_{b\textcircled1}=F_{Ares}\cdot 100\;mm=495,25\;N\cdot 100\;mm=\underline{\underline{49,53\;Nm}}$

8. Vergleichsmoment Welle I

$M_{VI}=\sqrt{M_{bI}\;^2+0,75(\alpha_{0} \cdot M_{tI})^2}$

Das Anstrengungsverhältnis α₀ beträgt 0,7 nach [F 3-7]. Das Torsionsmoment entspricht dem Drehmoment aus Aufgabe 1.

$M_{VI}=\sqrt{(49,53\;Nm)\;^2+0,75(0,7 \cdot 39,79\;Nm)^2}$

$M_{VI}=\underline{\underline{55,09\;Nm}}$

9. Durchmesser Welle I

Hier ist die zulässige Spannung mit 50 N/mm² bereits gegeben. Normalerweise ist das nicht der Fall. Außerdem sieht die Aufgabe vor, dass die komplette Welle nur einen Durchmesser hat. Deshalb haben wir auch nur ein Biegemoment ermittelt.

$\sigma _{bzul}=\frac{M_{b}}{W_{b}}=\frac{M_{b}\cdot 32}{\pi\cdot d^3}$

nach d umgestellt. M_v für M_b

$d=\sqrt[3]{\frac{M_{v}\cdot 32}{\sigma_{bzul}\cdot\pi}}$

$d=\sqrt[3]{\frac{55090\;Nmm\cdot 32\cdot mm^2}{50\;N\cdot\pi}}$

$d_{1}=22,39\;mm$

$d_{1gew}=\underline{\underline{22,4\;mm}} \;[TB \;1-16]$

10. Drehmoment Welle II

Das Drehmoment können wir über die Übersetzung anhand von z₁ und z₂ermitteln.

$i=\frac{z_{2}}{z_{1}}\Rightarrow z_{2}=z_{1}\cdot i=19\cdot 3,2=60,8$

$z_{2gew}=60 \;[TB\;1-16]$

$M_{TII}=M_{TI}\cdot\frac{z_{1}}{z_{2}}=39,79\;Nm\cdot\frac{60}{19}=\underline{\underline{125,66\;Nm}}$

11. Teilkreisdurchmesser d₂ und d₃

$d_{2}=z\cdot m=60\cdot 6\;mm=\underline{\underline{360\;mm}}$

$d_{3}=z\cdot m=25\cdot 8\;mm=\underline{\underline{200\;mm}}$

12. Zähnezahl z₄ und Durchmesser d₄

$z_{4}=i\cdot z_{3}=2,8\cdot 25=70$

$z_{4gew}=71 [TB \;1-16]$

$d_{4}=z\cdot m=71\cdot 8\;mm=568\;mm$

Achtung! Der Durchmesser darf nicht noch einmal angepasst werden, da er das Produkt aus Modul und Zähnezahl ist, sonst hätten wir wieder eine ungerade Zähnezahl.

13. Tangentialkraft F_t3 und Radialkraft F_r3

$F_{t3}=\frac{M_{tII}}{r_{3}}=\frac{125660\;Nmm}{100\;mm}=\underline{\underline{1256,6\;N}}$

$F_{r3}=tan(20\degree)\cdot 1256,6 \;N =\underline{\underline{457,36\;N}}$

14. Lagerkräfte für Lager C und D

Dieses Mal hat unser Getriebeplan zwei Zahnradpaare zu berücksichtigen.

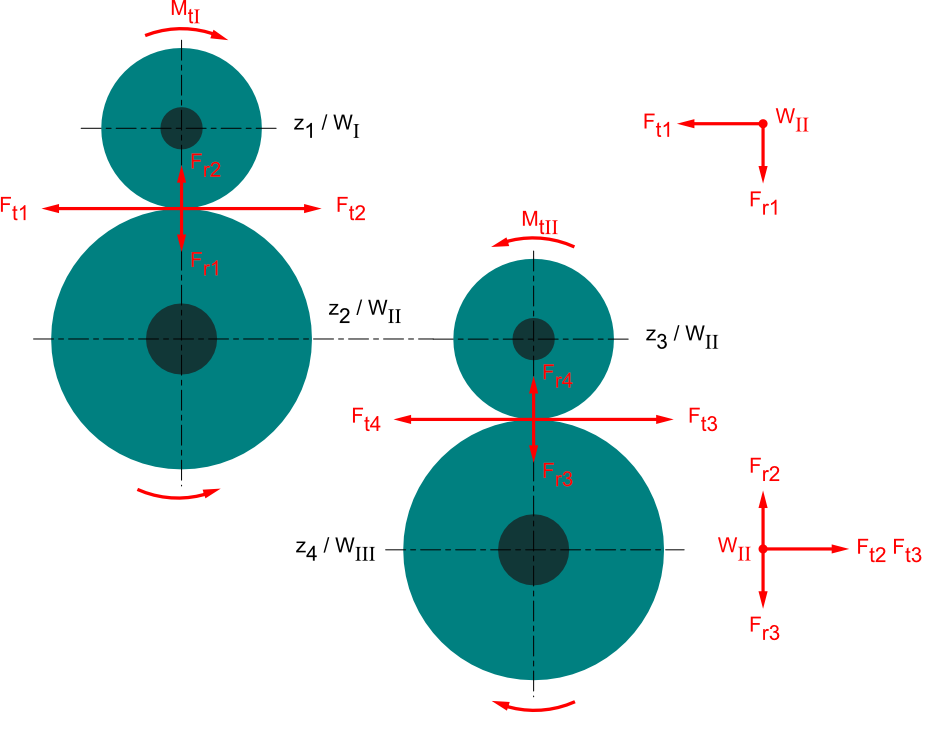
Auf der Welle II befinden sich Zahnrad 2 und 3. Das bedeutet wir beziehen alle Kräfte mit dem Index 2 und 3 in unsere Freikörperbilder mit ein.

$\Sigma M_{Cy}\circlearrowleft=0=F_{r2}\cdot 100\;mm-F_{r3}\cdot 200\;mm + F_{Dy}\cdot 300\;mm$

$F_{Dy}=\frac{-F_{r2}\cdot 100\;mm+F_{r3}\cdot 200\;mm}{300\;mm}$

$F_{Dy}=\underline{\underline{220,21\;N}}$

$\Sigma M_{Dy}\circlearrowleft=0=F_{r3}\cdot 100\;mm-F_{r2}\cdot 200\;mm - F_{Cy}\cdot 300\;mm$

$F_{Cy}=\frac{F_{r3}\cdot 100\;mm-F_{r2}\cdot 200\;mm}{300\;mm}$

$F_{Cy}=\underline{\underline{-16,93\;N}}$

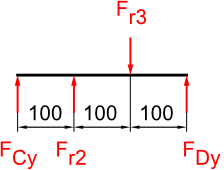
Negatives Vorzeichen kann ignoriert werden.

$\Sigma M_{Cx}\circlearrowleft=0=-F_{t2}\cdot 100\;mm-F_{t3}\cdot 200\;mm + F_{Dx}\cdot 300\;mm$

$F_{Dx}=\frac{F_{t2}\cdot 100\;mm+F_{t3}\cdot 200\;mm}{300\;mm}$

$F_{Dx}=\underline{\underline{1070,42\;N}}$

$\Sigma M_{Dx}\circlearrowleft=0=F_{t2}\cdot 100\;mm+F_{t3}\cdot 200\;mm - F_{Cx}\cdot 300\;mm$

$F_{Cx}=\frac{F_{t2}\cdot 200\;mm+F_{t3}\cdot 100\;mm}{300\;mm}$

$F_{Cx}=\underline{\underline{884,2\;N}}$

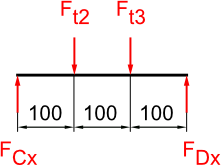
resultierende Kräfte

$F_{Cres}=\sqrt{F_{Cx}\;^2+F_{Cy}\;^2}$

$F_{Cres}=\sqrt{\left (884,2\;N\right )^2+(16,93\;N)^2}$

$F_{Cres}=\underline{\underline{884,36\;N}}$

$F_{Dres}=\sqrt{F_{Dx}\;^2+F_{Dy}\;^2}$

$F_{Dres}=\sqrt{\left (1070,42\;N\right )^2+(220,21\;N)^2}$

$F_{Dres}=\underline{\underline{1092,84\;N}}$

15. maximales Biegemoment Welle II

$M_{b\textcircled1}=F_{Cres}\cdot 100\;mm=884,09\;N\cdot 100\;mm=\underline{\underline{88409\;Nmm}}$

$M_{b\textcircled2}=F_{Dres}\cdot 100\;mm=1092,84\;N\cdot 100\;mm=\underline{\underline{109284\;Nmm}}$

$M_{b\textcircled{2}}=M_{bmax}$

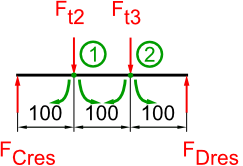
16. Vergleichsmoment Welle II

$M_{VII}=\sqrt{M_{bII}\;^2+0,75(\alpha_{0} \cdot M_{tII})^2}$

Das Anstrengungsverhältnis α₀ beträgt 0,7 nach [F 3-7].

$M_{VII}=\sqrt{(109,2\;Nm)\;^2+0,75(0,7 \cdot 125,66\;Nm)^2}$

$M_{VII}=\underline{\underline{133,15\;Nm}}$

17. Durchmesser Welle II

$d=\sqrt[3]{\frac{M_{v}\cdot 32}{\sigma_{bzul}\cdot\pi}}$

$d=\sqrt[3]{\frac{133150\;Nmm\cdot 32\cdot mm^2}{50\;N\cdot\pi}}$

$d_{2}=30,05\;mm$

$d_{2gew}=\underline{\underline{31,5\;mm}} \;[TB \;1-16]$

Nils

Artikel: 177

14 Kommentare

Oliver
6. Oktober 2024 / 19:51 Antworten
Hallo Nils
danke erst einmal für die übersichtliche Berechnung.
Ich habe jedoch eine Frage, wie du unter Punkt 8. „Vergleichsmoment Welle I“ bei der Vergleichsspannung (bei dem Torsionsanteil) auf den Wert 0,75 kommst, im Roloff/Matek steht dort statt 0,75 eine 3 (siehe Gleichung).
M_{VI}=\sqrt{(49,53\;Nm)\;^2+0,75(0,7 \cdot 39,79\;Nm)^2}
Vielen Dank schien einmal für die Antwort.
Grüße Oliver
- Nils
  6. Oktober 2024 / 20:42 Antworten
  Hallo Oliver,
  erst einmal vielen Dank für das Lob. Die Gleichung die du höchstwahrscheinlich meinst ist für die Vergleichsspannung. (Habe den Roloff Matek gerade nicht zur Hand).
  Was wir hier berechnen ist jedoch das Vergleichsmoment! Wie du diese Gleichung umstellen bzw. herleiten kannst habe ich in einem anderen Beitrag beschrieben.
  https://technikdoku.com/zusammengesetzte-beanspruchung/
  Ich hoffe das hilft dir weiter!
  Viele Grüße
  Nils
Piet Seibt
15. Mai 2024 / 15:45 Antworten
Hallo Nils,
ich denke bei der Berechnung der Wälzlager ist dir ein Fehler unterlaufen.
Die Tangentialkraft muss bei der Lagerberechnung nicht beachtet werden. Diese wirkt ja nicht auf die Wellen und somit muss doch nur die Radialkraft berücksichtigt werden oder?
Gruß Piet
- Nils
  15. Mai 2024 / 18:07 Antworten
  Hallo Piet,
  du hattest in diesem Beitrag hier kommentiert. Welches Beispiel meinst du bezogen auf Wälzlager?
  Viele Grüße
  Nils
  - Piet
    16. Mai 2024 / 10:41 Antworten
    Hallo Nils,
    vielen Dank für die schnelle Antwort. Ich meine in dem Beitrag bei Punkt 11 wird in der Abbildung gezeigt, dass die Tangentialkräfte von den Wälzlagern abgefangen werden, diese werden anschließend mit den Radialkräften in eine resultierende Kraft umgerechnet.
    Die Wälzlager nehmen aber nur die Radialkräfte auf, die Tangentialkräfte werden über das eingreifende Zahnrad abgeleitet oder?
    Vielen Dank im voraus.
    Gruß Piet
    - Nils
      16. Mai 2024 / 13:13 Antworten
      Bist du im falschen Beitrag? Im Punkt 11 werden die Teilkreisdurchmesser angegeben.
      - Piet
        16. Mai 2024 / 13:38
        Entschuldige mein Fehler, ich meine den Punkt 14.
      - Nils
        17. Mai 2024 / 17:13
        Das sind keine Wälzlager, sondern Zahnräder. Die nehmen Tangentialkräfte auf, dass ist korrekt, so wie es dargestellt ist.
Fritz
29. März 2024 / 16:50 Antworten
Hallo Nils,
Erstens, warum ist bei der Dimetrischen Darstellung die Radialkraft 1 auf das Zahnrad der Welle 1 gerichtet und bei dem Getriebeplan darunter auf das Zahnrad 2?
Zweitens, was würde sich an der Rechnung ändern, wenn die Wellen der Zahnräder nicht in einer Flucht liegen sonder bspw aus Platzgründen die Zwischenwelle höher liegt und es von der Vorderansicht sozusagen ein Dreieck bildet. Muss ich die Winkel zwischen den Zahnrädern dann einbeziehen oder kann ich das, da alles Radial ist weglassen und dein Beispiel wäre dann universal?
Vielen Dank
- Nils
  29. März 2024 / 17:17 Antworten
  Hallo Fritz,
  Kräfte können auf ihrer Wirkline darstellerisch verschoben werden, es spielt also vereinfacht gesehen keine Rolle ob die Kraft auf die Welle drückt. oder daran zieht.
  Was deine zweite Frage angeht. Lässt man die Gewichtskräfte außen vor (was wir in dieser vereinfachten Rechnung hier tun), sollte das keine Rolle spielen. Man dreht einfach das Koordinatensystem und schon hat man die selbe Rechnung. Ansonsten hast du recht. Man müsste dann jede schräge Kraft in ihre X und Y Komponente zerlegen.
  Ich hoffe es hilft dir weiter. Wichtig ist, im Zweifel, solltest du immer den Lehrer fragen, wie ihr die Fälle betrachten sollt! Die Beiträge hier bilden nur meinen Lernfortschritt ab und sind vielleicht nicht 1:1 auf jede Situation übertragbar.
Jako
29. Februar 2024 / 1:07 Antworten
Hallo Nils,
könntest du mir auch erklären wie ich die Axialkraft einer Zwischenwelle eines zweistufigen Stirnradgetriebes mit Schrägverzahnung berechne? (Schrägungsrichtung der Zahnräder ist so gewählt das die Axialkräfte z2 und z3 entgegengesetzt wirken.)
- Nils
  29. Februar 2024 / 7:30 Antworten
  Eine detaillierte Erklärung würde das Format eines Kommentars sprengen. Es lässt sich grob festhalten, desto größer der Schrägungswinkel, desto größer auch die Axialkraft. Der Schrägungswinkel lässt sich mit der Formel cos(beta) = pn/pt ermitteln.
Mata
7. Februar 2023 / 7:12 Antworten
Hallo Nils,
vielen Dank für deinen Beitrag, hat mir sehr geholfen!
Ich wollte dich fragen, warum man hier keine Gewichtskraft (m*g) der Welle bzw. des Zahnrads berücksichtigt.
Vielen Dank!
Gruß Mata
- Nils
  7. Februar 2023 / 10:47 Antworten
  Hallo Mata,
  es freut mich, dass dir der Beitrag helfen konnte. Du hast natürlich vollkommen recht. Jedoch handelt es sich hier viel eher um ein Anwendungsbeispiel aus meiner Techniker Weiterbildung. Dabei geht es weniger darum zu ermitteln, welche Kräfte wie ins System kommen, sondern eher darum zu sehen, wie man mit diesen umgeht. Ansonsten müssten ja auch Zahnräder ermittelt werden. Die Festigkeitsberechnung der Zahnräder ist auch nicht Teil dieses Beitrags und somit kennen wir die Masse dieser ja auch gar nicht.

Formelzeichen – Berechnung von Zahnradgetrieben

Formeln

Beispiel 1 – zweistufiges Stirnradgetriebe

Nils

14 Kommentare

Schreibe einen KommentarAntworten abbrechen