Zahnräder konstruieren.

Evolventenverzahnung

Formeln

Um ein Zahnrad zu konstruieren können folgende Formeln verwendet werden:

Modul m

Das Modul ist  eine Verhältniszahl resultierend aus der Teilung p und dem Kreisumfang π. Die Zahnradmodule sind nach DIN 780 genormt.

m=pπ

Teilung p

p=m·π

Teilkreisdurchmesser d

Der Teilkreisdurchmesser d errechnet sich aus dem Modul und der Zähnezahl z.

d=m·z

Zahnhöhe h

Die Zahnhöhe ergibt sich aus dem Modul und dem Kopfspiel c. Das Kopfspiel ist in der DIN 867 genormt und soll zwischen 0,1 · m und 0,3 · m liegen. Standardwerte sind z.B. 0,167 · m und 0,25 · m.

Achtung beim Kopfspiel c nicht vergessen den Faktor mit dem Modul zu multiplizieren!

h=2·m+c

Kopfhöhe ha

ha=m

Fußhöhe hf

hf=m+c

Kopfkreisdurchmesser da

da=d+2·mda=m·(z+2)

Fußkreisdurchmesser df

df=d–2·hf

Grundkreis db

db=d·cos(20°)

Fußrundung ϱf

ϱf=0,38·m

Achsabstand a

Der Achsabstand kann entweder durch die gegebenen Teilkreisdurchmesser errechnet werden:

a=d1+d22

Oder Anhand der Zähnezahlen in Kombination mit dem Modul:

a=m(z1+z2)2

Zahndicke sp

sp=ep=p2

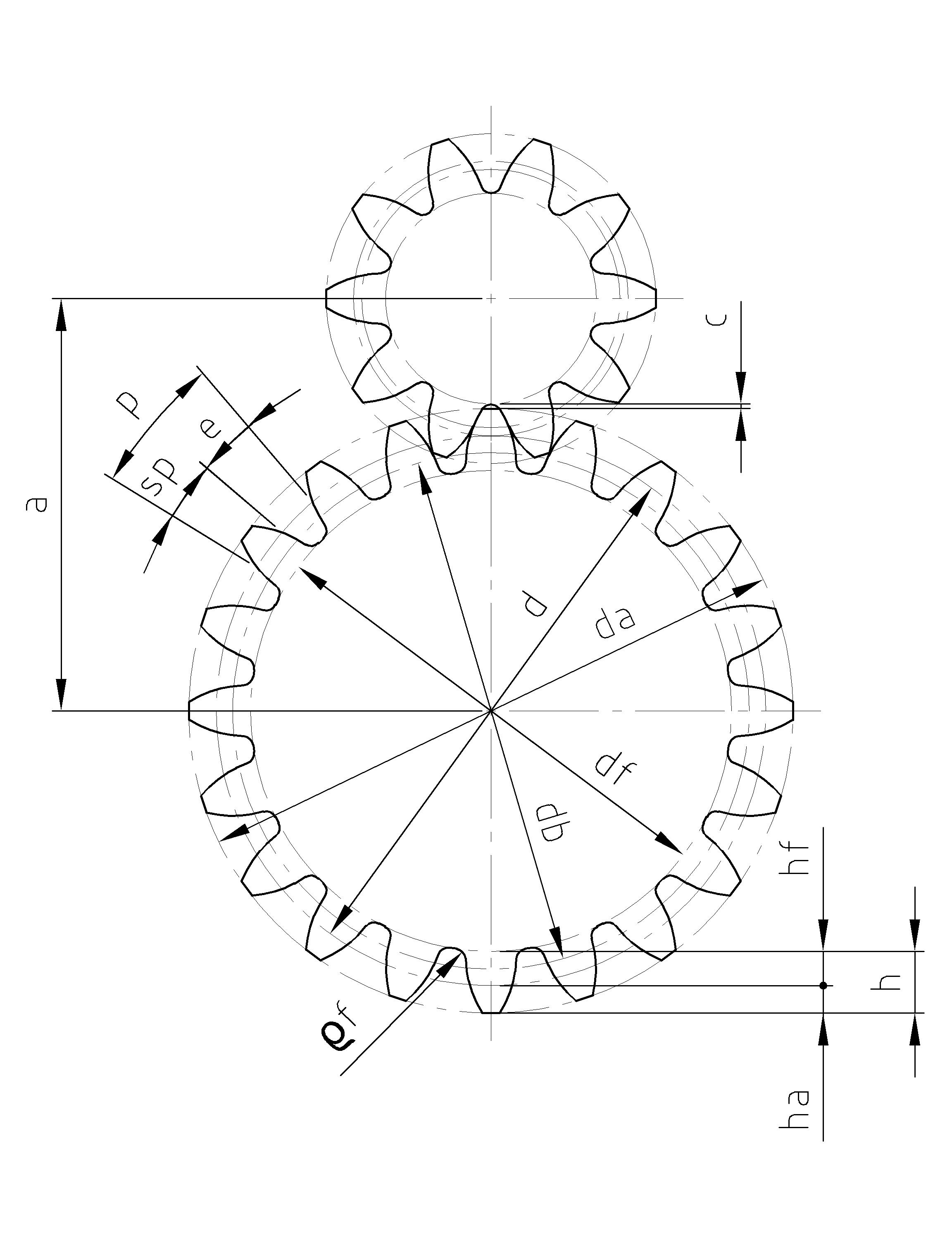
Zahnrad Abmessungen berechnen

 

 

Nils
Nils
Artikel: 178

38 Kommentare

    • In meinem praktischen Berufsleben hatte ich diesen Anwendungsfall noch nicht. Aus der Theorie heraus würde ich vermuten, dass man hier mit den Allgemeintoleranzen nach ISO 2768-mK auskommt. Aber das solltest du für einen praktischen Anwendungsfall nochmal prüfen.

  2. Hallo,

    Ich möchte gerne wissen, ob die Zahdicke die Breite eines Zahns ist? Wenn nicht, wie kann man die Breite eines Zahns berechnen?
    Außerdem interessiere ich mich für eine allgemeine Abschätzung der Masse (Volumen) eines Planetengetriebes, ohne ins Detail zu gehen. Diese hängt von der Geometrie ab. Könnten Sie mir bitte allgemeine Formeln dazu geben? Wie kann man die Masse bzw. das Volumen eines Planetengetriebes allgemein berechnen? Ich vermute, dass man das Volumen jedes Zahnrads (Sonnenrad usw.) berechnen sollte, aber wie man weiter vorgeht, weiß ich nicht. Es wäre sehr nett, wenn Sie mir dabei helfen könnten.

    • Hallo Kourosh,

      die Zahndicke sp ist nicht die Tiefe des Zahnrads, falls du das meinst. Formeln zur Volumenberechnung sind mir leider nicht bekannt. Ich würde das Zahnrad konstruieren und dann die Fläche ermitteln um diese dann mit der Dicke des Zahnrads zu multiplizieren.

    • Hallo.
      ich würde das Zahnrad herstellen, in einen Messbecher mit einer genau bestimmten Menge Wasser geben und dann schauen wie viel Wasser es verdrängt….
      Gruß Lothar

  3. Hallo
    Kann mir jemand bei der Suche nach einem Zeichner helfen welcher mir einen Zahnkranz mit Zähnen Innenliegend zeichnen kann .
    Danke

    • Hallo Thomas,

      wenn es „nur“ um eine zeichnerische Darstellung geht, kann ich dir ggf. weiter helfen. Dabei würden jedoch fertigungsspezifische Belange unberücksichtigt bleiben, da ich dafür nicht genug im Thema bin. Handelt es sich dabei um ein Hohlrad für ein Planetengetriebe?

      Viele Grüße
      Nils

      • Hallo Nils
        Danke für die rasche Antwort , ich möchte kurz klarstellen dass ich gerne bereit bin für die Unterstützung meinen Beitrag zu leisten .
        Ich würde Dir gerne Hand Zeichnungen zukommen lassen welche Du dann technisch aufbereiten kannst, anschließend brauche ich Zeichnungen in PDF welche in die Produktion gehen ,
        Für eine rasche Antwort wäre ich sehr dankbar .
        Gruß
        Thomas

  4. Hallo Nils,
    bin im „Eigenstudium“
    es steht überall, dass der Modul der Zahnkopfhöhe entsprechen „muss“. Warum eigentlich?… Normierung? (Theoretisch könnte man sich man sich ja z.B.: auch Zähne mit gleicher Dicke aber weniger Höhe bei gleichem Teilkreisdurchmesser vorstellen – also gleicher Modul – oder hab ich da etwas nicht kapiert?)

    • Hallo Raldo,

      ich gebe zu darüber habe ich mir noch nie Gedanken gemacht. Ich kann daher nur Erklärungsversuche liefern.

      Zum einen ist es genormt das stimmt. Zum anderen braucht man ja auch eine gewisse Flankenlänge zum abrollen. Schau dir mal zwei Zahnräder im Eingriff an. Wäre das Kopfspiel zu groß könnte der eine Zahn den anderen nicht weiter reichen. Wäre es zu klein würde es haken.

      Ich hoffe das hilft weiter.

  5. Hallo Nils,
    Ich möchte den Teilkreisdurchmesser der Innenverzahnung brechnen.

    Kann man mit deine Tools brechnen? Oder ist es nur für Zahnrad.

    Viele Grüße

    • …danke für die prompte Antwort. Die Zahnräder im Eingriff hab ich mir ziemlich genau angeschaut – es gibt dazu auch eine Reihe sehr schöner videoclips im Netz. Es ist auch klar, dass man das Vezahnungsgesetz einhalten muss, etc.
      Im guten alten Dubbel hab ich zur Zahnkopfhöhe = Modul in Klammern (normal) gefunden. Das spricht wohl für Normierung.

      Also – wenn es zum Beispiel der Werkstoff und die Zahnfußfestigkeit es erfordern würde, könnte man dann wohl z.B.: durchaus Zahnradverbindungen mit in der Proportion dickeren Zähnen, die dann einen geringeren Biegehebel aufweisen, vorsehen.

  6. Hallo Nils,
    ich finde deine Seite sehr hilfreich, danke schonmal! Doch wie komme ich denn auf die Rundungen, die die einzelnen Zähne haben? Ich möchte zwei gleich große Zahnräder aus Holz bauen. Meine Maße die ich dazu eingegeben habe sind m=16,59375 z=32 c=1,5. Ich brauche d=531 deswegen komme ich auf diese Maße. Die einzige Rundung die mit errechnet wird, ist ja die Fußrundung, doch wie kommt man auf die Rundung der einzelnen Zähne?
    LG Justine

  7. Hallo Nils,
    ich möchte mir Zahnräder aus Holz herstellen. Es ist für eine Holzräderuhr.
    Das Modul soll 2,35 sein.
    Wie kann ich die Werte für die Triebstockverzahnung ermitteln?

    Gruß
    Kalli

  8. Hallo Nils,

    Gibt es Vorgaben bezüglich des Verhältnis zwischen Teilkreisdurchmessers und der Größe Durchgangslochs des Zahnrades?

    Freundliche Grüße Malte

    • Die Kranzdicke, also der Bereich zwischen Fußkreis und dem Zahnkranz (Wellenbohrung) soll laut Roloff Matek (24. Auflage) ≥ 3,5 · m betragen.

  9. Moin,
    Ich habe eine Frage, und zwar; Darf der Teilkreisdurchmesser ZB. 16.87mm sein, oder muss/soll es 17 mm aufgerundet werden ?
    Danke

    • Hallo Nima,

      theoretisch kann man ja jedes Zahnrad in beliebiger Größe anfertigen (lassen). In der Praxis würde man ein Zahnrad aber kaum auf ein Hundertstel genau anfertigen. Erstens aufgrund der Fertigungstoleranzen und zweitens weil der Konstrukteur ja bei der Auslegung/Berechnung des Zahnradgetriebs ja auch einen gewissen Spielraum hat.

  10. Guten Tag mein Name ist Jürg. Ich habe eine tech.Frage die mich schon jahrelang beschäftigt!
    Es betrifft den Ravignaux Planetensatz im Automatic-Getriebe eines Opel Omega 24V 3lt. (stärkste Ausführung) Baujahr ca.1990-95 in 4 Stufen Ausführung. Meine Frage: Warum müssen die Planetenrädermarkierungen mit den Markierungen auf dem Planetenträger ausgerichtet werden?
    Wird nicht ausgerichtet, so kann nur eines der 2 Sonnenräder eingefahren werden das andere Sonnenrad klemmt! Hat das mit der Zähnezahl oder der Formgebung der Zahnräder zu tun? Bei den schwächeren Motoren sind keine Markierungen vorhanden! Vielen Dank Jürg Jahrgang 1950

    • Hallo Jürg,

      leider kann ich dir diese Frage nicht beantworten. Die Planetengetriebe, die ich kenne haben alle gleich große Planetenräder, sowohl was die Anzahl der Zähne angeht, als auch deren Durchmesser. Haben die Zahnräder denn eine Schrägverzahnung?

    • Hallo Nils, ja alle Zahnräder haben die übliche Schrägverzahnung. dieser Planetensatz besteht aus Planetenträger mit 4 langen Planetenräder und 4 kurzen Planetenräder wobei diese miteinander im Eingriff sind.Das kleine Sonnenrad treibt die kurzen Planetenräder an und diese treiben die langen Planetenräder an,welche im Eingriff mit dem Grossen Sonnen sind.Das Hohlrad hat für diese Fragenstellung keine Bedeutung! Wird das Kleine Sonnenrad eingesetzt,so lässt sich das grosse Sonnenrad nur einige Millimeter einsetzen und dann klemmt es. Wird das Grosse zuerst eingesetzt,so klemmt das Kleine Planetenrad! Vielen Dank und freundliche Gruss Jürg

  11. Hallo Nils,

    ich habe eine Frage aus der Praxis. Den Durchmesser eines Zahnrades mit grader Anzahl an Zähnen kann man mit einer Bügelmessschraube direkt messen, aber was ist, wenn die Anzahl der Zähne ungrade ist. Wie Kann ich die Höhe zwischen zwei Zähnen berechnen, um diese dann vom Außendurchmesser abziehen zu können? Zumbeispiel h= r (1 – cos alpha/2), wie finde ich alpha raus?
    Ich habe das Modul, Außendurchmesser, Zähnezahl, Angrifswinkel, Teilkreisdurchmesser, Fußkreis.

    • Hallo Chris,
      ich verstehe die Frage nicht. Du schreibst doch, dass der Außendurchmesser zu deinen bekannten Werten gehört? Außerdem kannst du diesen anhand des Teilkreisdurchmessers und dem Modul errechnen. Denkst du da gerade zu kompliziert, oder habe ich da etwas falsch verstanden?

      Falls du dennoch alpha wissen möchtest, kannst du die Gleichung nach alpha umstellen.
      α=arccos(((-2·h+2·r) / r))

      • Hallo,
        in deiner Formel ist h bekannt. Ich will aber h bestimmen. Die Bügelmessschraube soll mir sagen, wie weit der Außebdurchmesser vom Idealmass abweicht im Bereich 1/1000 mm. Eine Seite liegt auf dem Radius, die zweite Seite liegt auf den Kanten zweiter Zähne. Ich suche jetzt eine Formeldie ich sowohl bei einem Durchmesser von 17 mm mit Modul 0.8 einsetzen kann, sowie einen Durchmesser von 240 mm mit Modul 5 zum Beispiel.

        • Du kennst den Modul und den Durchmesser. Also kennst du doch auch die Zähnezahl. 360° durch die Zähnezahl ist der Winkel der sich für die Teilung ergibt.

          Außerdem kannst du doch auch den Außendurchmesser errechnen. Die Formel steht auch oben.

  12. Hallo Nils
    Klasse Seite !!!
    Ich bin Konstrukteur und habe ein kleines Problem mit einem Planetenradgetriebe, vielleicht kannst Du mir einen Tipp geben.
    Wir bestellen es seit Jahren bei einem Zulieferer, den gibt es allerdings leider nicht mehr, und jetzt versuche ich aus dem Modell (STEP) eine Fertigungszeichnung zu generieren.
    Bekomme aber die Profil-Verschiebung nicht heraus.
    Hast du eine Idee?
    Mfg Alex

    • Hallo Alex,

      erst einmal vielen Dank für das Lob.

      Ich muss zugeben, dass sich mein Wissen um die Zahnräder ausschließlich auf die Theorie beschränkt, da ich im Anlagenbau tätig bin. Deswegen wäre es auf jeden Fall empfehlenswert sich da Hilfe von einem Fachmann einzuholen. So ein Zahnrad kann je nach Größe, Werkstoff und Oberflächenbehandlung ja schon mal etwas teurer werden. 🙂

      Die Profilverschiebung ergibt sich aus einem Profilverschiebungsfaktor der mit dem Modul multipliziert wird. Um diesen Betrag wird die Profilbezugslinie entweder positiv oder negativ versetzt. Daraus ergeben sich dann auch andere Maße welche sich auf den Teilkreisdurchmesser d beziehen.

      Wichtig ist aber natürlich, dass die Profilverschiebung an die umliegenden Zahnräder bzw. dem äußeren Zahnkranz im Planetengetriebe angepasst ist.

      ggf. kannst du anhand der STEP Datei erkennen ob es sich dabei um den Norm- oder den Fertigungsstand handelt, wenn du mal durchrechnest ob sich anhand der Werte eine Ganzzahl der Zähne ergeben würde?

  13. Die Mathematik hinter Getriebeauslegung und Zahnräder ist echt Wahnsinn. Ich kann damit nicht anfangen. Diese Gleichungen sind aber dafür sehr hilfreich.

  15. Hallo Nils, danke für die hilfreiche Seite.

    Ich habe festgestellt, dass je größer z wird, sich der Fußkreis dem Grundkreis annähert bis er irgendwann größer ist. Ich glaube da stimmt was nicht?!

    gruß Rene

    • Hallo Rene,

      vielen Dank für die Anmerkung. Ich werde das mal prüfen und melde mich dann hier wieder.

      Viele Grüße
      Nils

      • Habe jetzt mal verschiedene Stirnräder versucht und du hast recht. Die Formeln habe ich noch mal überprüft und die sollten stimmen (Quelle: Hoischen). Ich denke das ab einer gewissen Zähnezahl in Abhängigkeit zum Durchmesser bzw. der Teilung gewisse Verhältnisse nicht möglich sind. Hast du bei deinen Tests die genormten Kopfspiele und Modul verwendet?

        Desweiteren handelt es sich bei diesen Formeln um die zeichnerische Konstruktion von Zahnrädern. Ich denke, wenn man das Thema näher betrachten möchte, kommt man nicht drum herum sich die DIN ISO 21771 und ggf. andere Normen dazu anzuschauen (Abmessungen, Toleranzen etc.)

        Solltest du noch weitere Fragen haben oder einen spezifischen Anwendungsfall haben, bei dem du Hilfe brauchst, sag Bescheid. 🙂

  16. Hey ,

    guter Blog , ich Beginn mit der Techniker Ausbildung zum Maschinenbauer und finde das sehr hilfreich 👌🏼

    Mit freundlichen Grüßen

    • Hallo Daniel,

      es freut mich, dass dir der Blog gefällt. Solltest du Fragen oder Anmerkungen haben, lass es mich wissen! 🙂

      Viele Grüße
      Nils

Schreibe einen Kommentar

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert

5 − eins =