Bei der Berechnung von Schweißverbindungen ist die Konstruktion der Schweißverbindung zu betrachten und zu analysieren. Im Maschinenbau können z.B. ganz andere Berechnungsgrundlagen vorliegen als z.B. im Stahlbau oder Anlagen- Apparatebau
Allgemeine Berechnung von Schweißverbindungen
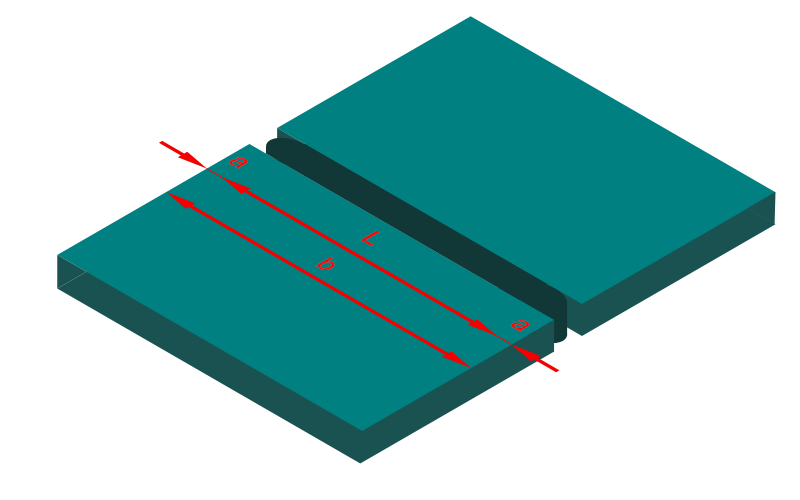
Stumpfnähte (Maschinenbau)
Bei durchgeschweißten Stumpfnähten wird im allgemeinen davon ausgegangen, dass diese genauso tragfähig sind, wie das schwächere der zu verbindenden Bauteile, wenn die Schweißzusätze korrekt gewählt wurden und die Schweißnaht fehlerfrei geschweißt wurde. Eine eventuelle Nahtüberhöhung bleibt dabei unberücksichtigt.
Beispiele
| I-Naht | 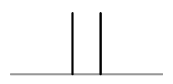 |
| V-Naht | 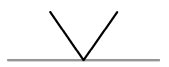 |
| Y-Naht | 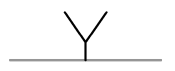 |
| HV-Naht | 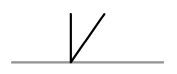 |
| HY-Naht | 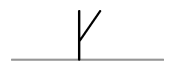 |
| U-Naht | 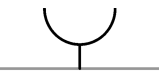 |
| HU-Naht |  |
Sind Stumpfnähte nicht durchgeschweißt, sind diese in der Regel wie Kehlnähte mit tiefem Einbrand zu berechnen.
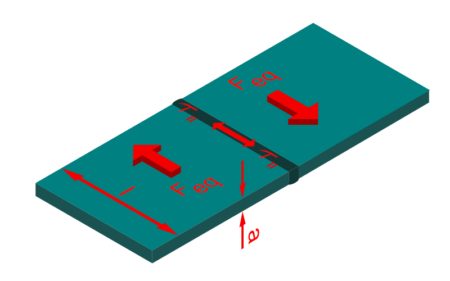
Für die wirksame Länge der Schweißnaht wird auf beiden Seiten eine Schweißnahtdicke abgezogen, da hier in der Praxis ein Krater entsteht. Verhindert werden kann das durch Auslaufbleche. Werden diese verwendet müssen die Endkrater nicht abgezogen werden.
Werden Auslaufbleche verwendet, oder ist die Nahtumlauf so gilt.
Die Querschnitte der Schweißnähte werden dann genauso auf Zug, Biegung oder Torsion beansprucht wie ein ungeschweißtes Bauteil.
Formelzeichen
| Formelzeichen | Bezeichnung | Einheit |
| σ⊥ | Normalspannung senkrecht zur Schweißnahtachse in der Kehlschnittfläche | N/mm² |
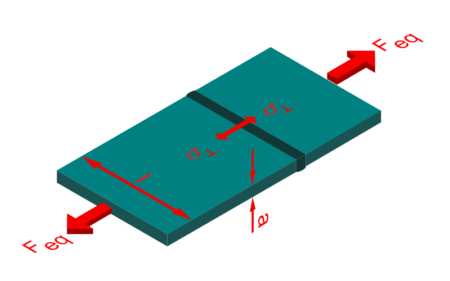
| Feq | äquivalente Kraft | N |
| Fm | Mittelkraft | N |
| KA | Anwendungsfaktor / Stoßfaktor | oE |
| Fa | Kraftamplitude (Ausschlag) | N |
| a | wirksame Dicke von Kehlnähten bzw. Stumpfnähten | mm |
| l | wirksame Länge der Schweißnaht | mm |
| σwzul | zulässige Normalspannung für die Schweißnaht | N/mm² |
| σw zul MKJ | zulässige Normalspannung für die Schweißnaht aus MKJ Diagramm | N/mm² |
| κ | Grenzspannungsverhältnis | oE |
| b | Dickenbeiwert | oE |
| τ∥ | Schubspannung in der Ebene der Kehlschnittfläche parallel zur Schweißnahtachse | N/mm² |
| τwzul | zulässige Schubspannung für die Schweißnaht | N/mm² |
| τw zul MKJ | zulässige Schubspannung für die Schweißnaht aus MKJ Diagramm | N/mm² |
| τ∥t | Torsionsspannung der Kehlschnittfläche parallel zur Schweißnahtachse | N/mm² |
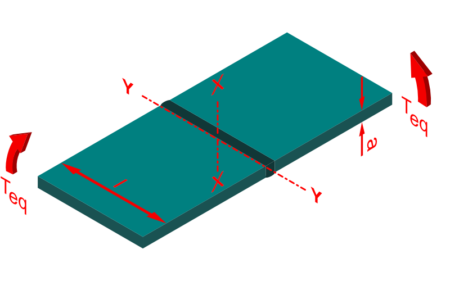
| Teq | äquivalentes Torsionsmoment | Nmm |
| Wwt | Widerstandsmoment der Schweißnaht | mm³ |
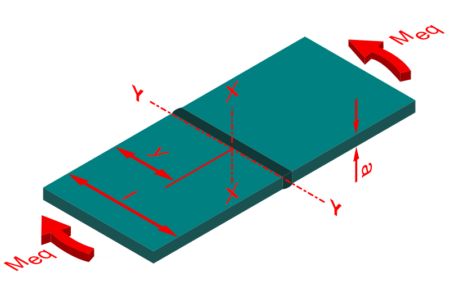
| Meq | äquivalentes Biegemoment | Nnn |
| Iw | Flächenmoment 2. Grades der Schweißnaht | mm4 |
| y | Abstand bei Biegeträgern der betrachteten Querschnittsstelle der Trägerachse x-x | mm |
| Aw | wirksame Fläche der Schweißnaht | mm² |
Spannungsarten
Für äquivalente Kräfte Feq gilt:
bzw. ohne Mittellast:
KA siehe DIN 3990-1 bzw. RM TB 3-5
Zug (Normalspannung)
RM FS 6-53
Biegung hochkant (Normalspannung)
RM FS 6-56
Diese Gleichung lässt sich etwas vereinfachen. Zunächst stellen wir fest, dass Iw = Ix ist, da es sich um eine Biegung um die „starke“ Achse handelt . Dafür finden wir eine Formel im Roloff Matek.
Die Breite b ist unser a und die Höhe h ist unser l
Diese Formel setzen wir in unsere Hauptgleichung ein.
y ist laut RM der Abstand von der betrachteten Querschnittsstelle von der Achse x-x. Dies könnte man also auch als l/2 sehen.
Kürzen wir das Ganze noch etwas ein.
Das Ergebnis sieht dann so aus. Wir brauchen also Iw und y nicht mehr vorher ausrechnen.
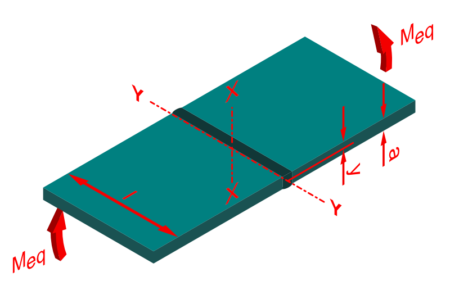
Biegung flachkant (Normalspannung)
RM FS 6-56
Hier können wir selbstverständlich die selbe Kürzung vornehmen. Nur das wir statt Ix nun Iy wählen müssen und y entsprechend gedreht werden muss. Dies ergibt dann.
Schub (Schubspannung)
Torsion (Torsionsspannung)
zulässige Spannung für die Schweißnaht
zulässige Normalspannung
zulässige Schubspannung
Berechnung der zulässigen Spannungen:
- Grenzspannungen aus den vorliegenden Einwirkungen und Widerstandsgrößen ermitteln
- Spannungsverhältnisse berechnen
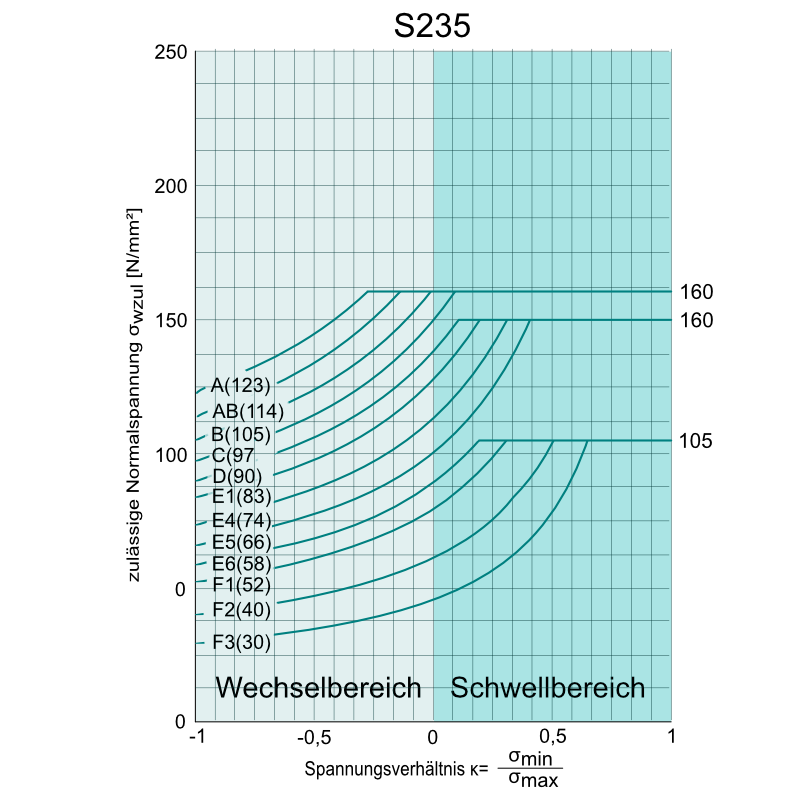
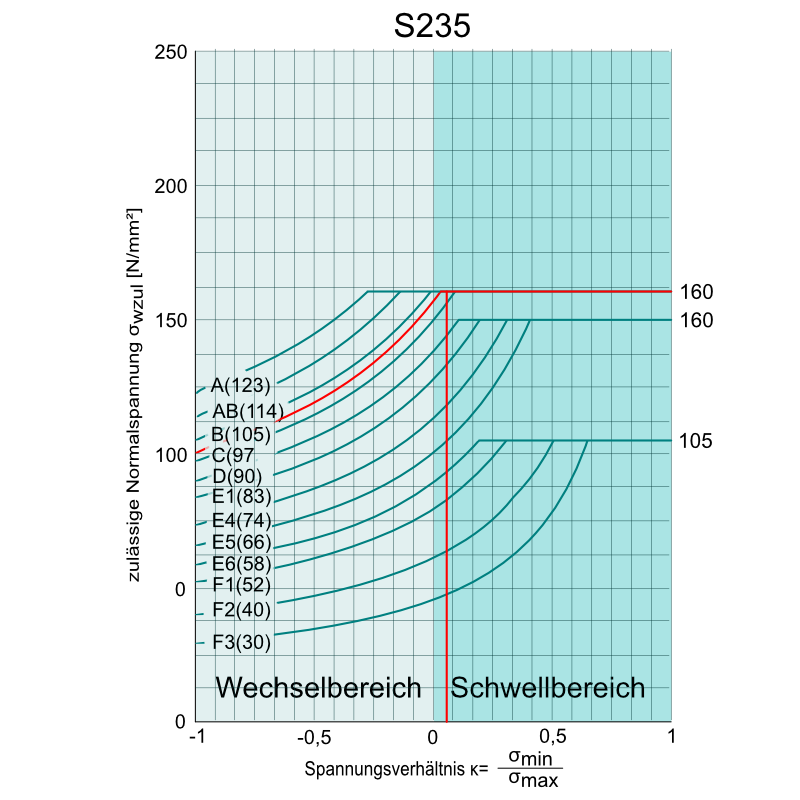
- Kerbfalllinie unter Berücksichtigung von Stoß-, Naht- und Beanspruchungsart ermitteln. (RM TB 6-11 / DVS 1612)
Linien A bis F2 ⇒ Normalspannungen, Linien G+ bis H- für Schubspannungen - zulässige Spannungen ablesen.
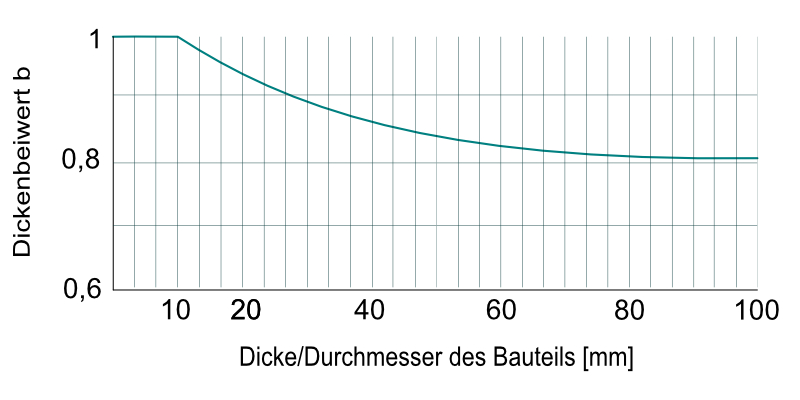
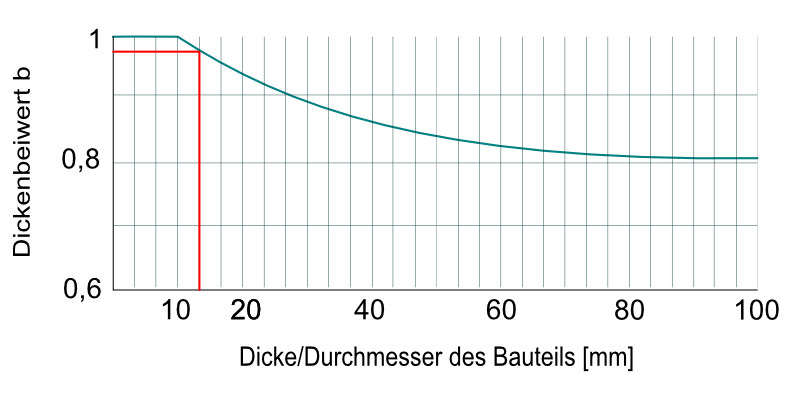
in Abhängigkeit von κ und der Stahlsorte in dem MKJ-Diagrammen (RM TB 6-12b1,b2), oder rechnerisch nach (RM TB 6-12a). - zulässige Spannungen berechnen unter Berücksichtigung von dem Dickenbeiwert b nach (RM TB 6-13). Bei t ≤ 10 mm ist b = 1
MKJ Diagramme
Dickenbeiwert
Regelwerke
Allgemein
Maschinenbau
Hier gibt es keine speziellen Regelwerke. Es werden hier allgemeine Spannungsnachweise durchgeführt. Es können natürlich auch Regelwerke anderer Fachgebiete wie dem Stahlbau oder dem Anlagenbau zur Anwendung kommen.
Für die Ermittlung werden oft noch zusätzliche St0ßfaktoren und Schwingbeiwerte berücksichtigt.
Bauwerke / Stahlbau
Tragwerke im Kranbau
DIN 15 018, T1 und T2
Anlagenbau
Beispiel Gelenköse
Eine Gelenköse hat eine Zuglast FZ von 80 kN zu heben. Außerdem treten wechselnde Belastungen Fa von bis zu 50 kN auf. Der Betriebsfaktor KA ist mit 1,4 vorgegeben. Das Blech aus dem die Öse gefertigt wurde ist 18 mm dick. Die Schweißnaht soll auf der vollen Länge geschweißt und kerbfrei bearbeitet werden. Die Dauerfestigkeit der Naht ist nachzuweisen, wenn sie 100 % durchstrahlt wird. Es handelt sich bei beiden Blechen um den Werkstoff S235.
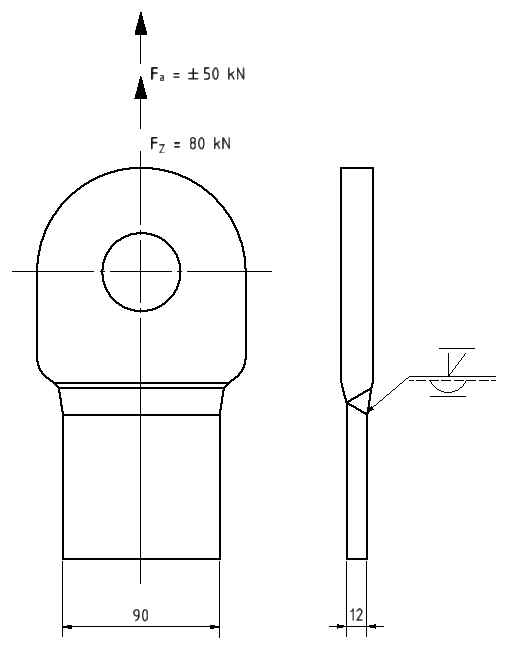
äquivalente Kräfte
maximale äquivalente Kraft
minimale äquivalente Kraft
Schweißnahtnormalspannung
maximale Spannung
minimale Spannung
Spannungsverhältnis
Aus der DVS Richtlinie 1612 lesen wir ab, dass es sich um die Kerbfalllinie B- handelt. Diese liegt 1,04 mal niedriger als die Linie B. Für uns macht dies jedoch an dieser Stelle keinen Unterschied, da wir bei beiden Kurven noch in die maximal zulässige Spannung von 160 N/mm² rein laufen.
Der Dickenbeiwert beträgt ca. 0,98
Das Bauteil ist dauerfest!