zusammengesetzte Beanspruchung

Die zusammengesetzte Beanspruchung ist die Zusammensetzung mehrerer Beanspruchungen in einem Bauteil. Wir kennen bereits die Beanspruchungen Zug (Normalspannung σ), Druck (Normalspannung σ),  Biegung (Normalspannung σ) und die Torsion (Tangentialspannung τ). Doch was ist, wenn mehrere Beanspruchungen gleichzeitig auftreten? Bei Zug/Druck und Biegung können wir die Spannungen addieren, da diesen Normalspannungen zu Grunde liegen. Schub und Torsion ebenfalls. Bei Biegung und gleichzeitiger Torsion geht das leider nicht. Die Biegung ist eine Normalspannung und wirkt orthogonal auf den Querschnitt, während die Tangentialspannung in axialer Richtung im Querschnitt wirkt. Eine einfache Addition ist deswegen nicht möglich.

Dies erkennt man allein schon an den unterschiedlichen Modulen, welche wir bei Normalspannungen und Tangential- Schubspannungen annehmen. Während der Normalspannung das Elastizitätsmodul E (Stahl 210000 N/mm²) zugrunde liegt, berücksichtigen wir bei Schub das Schubmodul G (Stahl 81000 N/mm²). Roloff Matek TB 1-1

Vergleichsspannung

Um diese Unterschiede zu berücksichtigen wird eine Vergleichsspannung (ideelle Spannung) ermittelt. Diese wurde aus der Hypothese der größten Gestaltänderungsenergie ermittelt, da diese Versuchen entsprechend gut übereinstimmt. Bei diesen Versuchen wurde festgestellt, dass Tangentialspannungen das Bauteil deutlich höher beanspruchen als Normalspannungen. Dies wird in der Gleichung durch den Faktor 3 dargestellt.

${\sigma }_v=\sqrt{{{\sigma }_b}^2+3{\left({\alpha }_0·{\tau }_t\right)}^2}\le {\sigma }_{bzul}$

Vergleichsmoment

Das Problem dabei ist jedoch, dass wir dazu den Durchmesser kennen oder einen annehmen müssen. Um dieses Problem zu umgehen, lässt sich aus der Gleichung der Vergleichsspannung ein Vergleichsmoment ableiten.

${\sigma }_v=\sqrt{{{\sigma }_b}^2+3{\left({\alpha }_0·{\tau }_t\right)}^2}$

Für σ_b und τ_t kennen wir die Gleichungen der Grundbeanspruchungsarten.

${\sigma }_b=\frac{M_b}{W_b} und {\tau }_t=\frac{M_t}{W_t}$

Jetzt haben wir jedoch noch das Problem, dass wir mit W_b und W_t zwei unterschiedliche Variablen haben. Schaut man sich die Formeln dafür aber an, erkennen wir, dass W_t doppelt so groß ist wie W_b also setzen wir für W_b einfach W_b ein und für W_t nehmen wir 2·W_b

$$\begin{gathered} 1) {\sigma }_v=\sqrt{{{\sigma }_b}^2+3{\left({\alpha }_0·{\tau }_t\right)}^2} \\ 2) {\sigma }_v=\sqrt{{\left(\frac{M_b}{W_b}\right)}^2+3{\left({\alpha }_0·\frac{M_t}{W_t}\right)}^2} \\ 3) {\sigma }_v=\sqrt{{\left(\frac{M_b}{W_b}\right)}^2+3{\left({\alpha }_0·\frac{M_t}{2·W_b}\right)}^2} \end{gathered}$$

Soweit so gut. Jetzt wird es etwas kniffliger. Nun müssen wir die Quadrierung unter dem Bruch ausklammern. Dazu quadrieren wir jedes Monom einzeln und lassen die Klammern weg. Achtung! auch die 2 unter dem M_t und α₀ müssen quadriert werden. Die 3 vor α₀ steht jedoch nicht in der Klammer und bleibt wie sie ist.

$4) {\sigma }_v=\sqrt{\frac{{M_b}^2}{{W_b}^2}+{3{\alpha }_0}^2·\frac{{M_t}^2}{{4W_b}^2}}$

Jetzt lösen wir die Brüche auf, indem wir W_b vor den Bruch schreiben. Wir erinnern uns eine Quadrierung ist die Äquivalenzumformung eines Bruchs.

$5) {\sigma }_v=\frac{1}{W_b}\sqrt{{M_b}^2+{3{\alpha }_0}^2·\frac{{M_t}^2}{4}}$

Dann schreiben wir die Gleichung ins Reine indem wir die 4 zu der 3 in den Bruch packen, beide sind nicht quadriert. α₀ und M_t jedoch schon. Diese fassen wir in einer quadrierten Klammer zusammen.

$6) {\sigma }_v=\frac{1}{W_b}\sqrt{{M_b}^2+\frac{3}{4}· \left({\alpha }_0·{M_t}^2\right)}$

Nun lösen wir noch die Brüche auf, indem wir W_b multiplizieren und den Bruch in der Wurzel in eine Dezimalzahl umwandeln.

$7) {\sigma }_v·W_b=\sqrt{{M_b}^2+0,75· \left({\alpha }_0·{M_t}^2\right)}$

Schauen wir uns die Biegehauptgleichung noch mal an.

${\sigma }_b=\frac{M_b}{W_b} \Rightarrow M_b={\sigma }_b·W_b$

Daraus lässt sich das Produkt vor dem Gleichzeichen in ein Vergleichsmoment umwandeln.

${\sigma }_v=\frac{M_v}{W_b} \Rightarrow M_v={\sigma }_v·W_b$

daraus folgt.

$8) M_v=\sqrt{{M_b}^2+0,75· \left({\alpha }_0·{M_t}^2\right)}$

Diese Gleichung lässt sich nun auch ohne einen bekannten Durchmesser nutzen.

Formelzeichen

Formelzeichen	Bedeutung	Einheit
σV	Vergleichsspannung	N/mm²
σb	Biegespannung	N/mm²
τt	Torsionsspannung	N/mm²
α0	Anstrengungsverhältnis	oE
σbGrenz	Grenzfestigkeit (Biegung)	N/mm²
τtGrenz	Grenzfestigkeit (Torsion)	N/mm²
MV	Vergleichsmoment	Nmm bzw. Nm
KA	Anwendungsfaktor / Betriebsfaktor	oE
SF	Sicherheit gegen Fließen	oE

Formeln

Vergleichsspannung nach der Gestaltänderungsenergiehypothese

Für die zusammengesetzte Beanspruchung Biegung und Torsion

${\sigma }_v=\sqrt{{{\sigma }_b}^2+3{\left({\alpha }_0·{\tau }_t\right)}^2}\le {\sigma }_{bzul}$

Anstrengungsverhältnis

Das Anstrengungsverhältnis berücksichtigt die Kombination der verschiedenen Lastfälle, die auftreten können.

${\alpha }_0=\frac{{\sigma }_{bGrenz}}{1,73·{\tau }_{tGrenz}}$

Für Wellen aus Stahl ist dieses jedoch näherungsweise bekannt.

α_{0 ≈} 0,7 bei Biegung, wechselnd wirkend und Torsion ruhend (schwellend) Standardfall für Wellen

α_{0 ≈} 0,1 bei Biegung, wechselnd wirkend und Torsion wechselnd

α_{0 ≈} 1,5 bei Biegung, ruhend (schwellend) wirkend und Torsion wechselnd

Vergleichsmoment

Für die zusammengesetzte Beanspruchung Biegung und Torsion

$M_v=\sqrt{{M_b}^2+0,75· \left({\alpha }_0·{M_t}^2\right)}$

Beispiel 1 Hubschlitten:

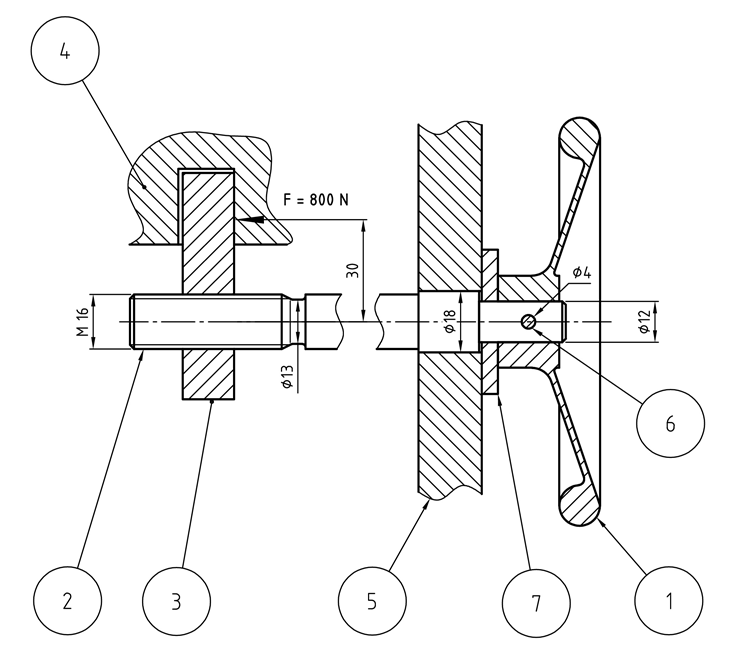
Wird das Handrad (1) gedreht, dreht sich auch die Gewindespindel (2), da diese über den Stift (6) formschlüssig verbunden ist. Dadurch wird der Mitnehmer (3) und damit auch der Schlitten (4) linear bewegt. Die Spindel ist im Gehäuse (5) gelagert. Das Handrad ist durch die Anlaufscheibe (7) axial gegen das Gehäuse (5) gelagert.

Der Schlitten wird durch eine Kraft von 800 N belastet. Das Handrad wird mit einem Drehmoment von 3 Nm betrieben. Wir gehen in diesem Beispiel von einer statischen Belastung aus. Als Werkstoff nehmen wir den Maschinenbaustahl E295 an. Die Streckgrenze beträgt 300 N/mm² (RM TB 1-1) . Aufgrund möglicher leichter Stöße im Betrieb berücksichtigen wir einen Betriebsfaktor K_A von 1,25. Die Sicherheit gegen Fließen S_F ist vom Kunden mit 1,7 vorgegeben.

Wir sollen nun mögliche gefährdete Querschnitte der Gewindespindel (2) analysieren und den Festigkeitsnachweis erbringen.

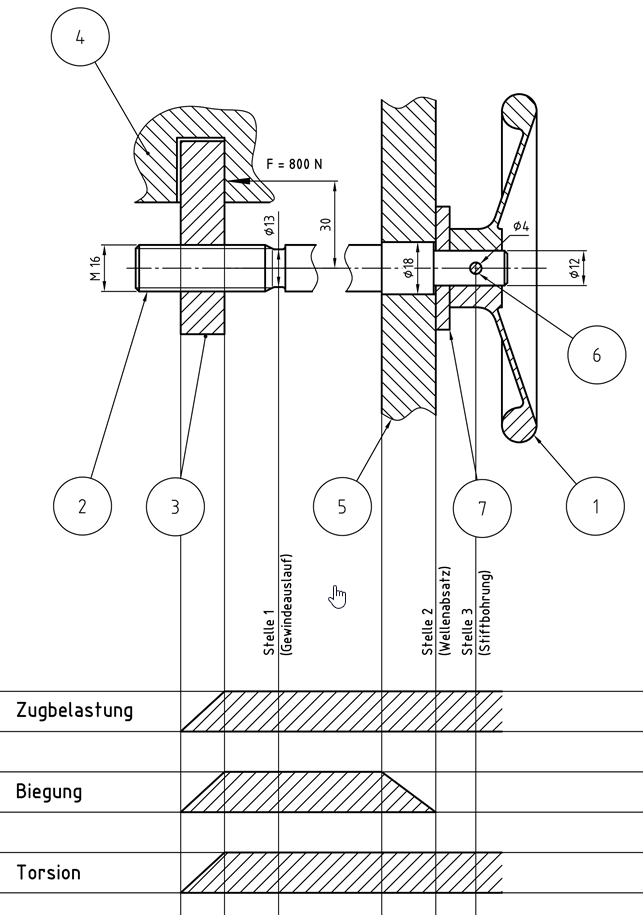
Wir haben drei mögliche Stellen als gefährdete Querschnitte analysiert und festgehalten wo welche Belastungen wirken. Die Biegebeanspruchung wird durch die Radiallager in Form des Mitnehmers (3) und des Gehäuses (5) aufgenommen und wirkt am stärksten zwischen diesen. Zug- und Torsionsbeanspruchung wirken auch erst ab dem Mitnehmer (3) da vor diesem ja nichts an der Spindel zieht. Diese Beanspruchungen wirken jedoch über das Gehäuse (5) hinaus, da es keine Axialkräfte aufnimmt.

Wir haben also an allen drei ausgemachten Stellen eine zusammengesetzte Beanspruchung.

1. zusammengesetzte Beanspruchung aus Zug, Biegung und Torsion
2. zusammengesetzte Beanspruchung aus Zug und Torsion
3. zusammengesetzte Beanspruchung aus Zug und Torsion

Stelle 1: zusammengesetzte Beanspruchung aus Zug, Biegung und Torsion

Zug

${\sigma }_z=\frac{K_A·F}{A}\Rightarrow \frac{K_A·F·4}{\mathrm{\pi }·{\mathrm{d}}^2}$

Werte einsetzen

$$\begin{gathered} {\sigma }_z=\frac{1,25·800 N·4}{\mathrm{\pi }·{13}^2·m{m}^2} \\ {\sigma }_z=7,53 N/mm² \end{gathered}$$

Biegung

${\sigma }_b=\frac{M_b}{W_b} \Rightarrow {\sigma }_b=\frac{K_A·M_b·32}{\mathrm{\pi }·{\mathrm{d}}^3}$

Werte einsetzen

$$\begin{gathered} {\sigma }_b=\frac{1,25 · 800 N · 30 \cancel{mm }· 32}{\mathrm{\pi }·{13}^3 {\mathrm{mm}}^{\cancel{3} 2}} \\ {\sigma }_b=139,09 N/mm² \end{gathered}$$

Torsion

$$\begin{gathered} {\tau }_t=\frac{K_A·M_t}{W_t} \Rightarrow \frac{K_A·M_t·16}{\mathrm{\pi }·{\mathrm{d}}^3} \\ {\tau }_t=\frac{1,25·3000 N\cancel{mm}·16}{\mathrm{\pi }·{13}^3 {\mathrm{mm}}^{\cancel{3} 2}} \\ {\tau }_t=8,69 N/mm² \end{gathered}$$

zusammengesetzte Beanspruchung aus Zug, Biegung und Torsion

$$\begin{gathered} {\sigma }_v=\sqrt{{\left({\sigma }_b+{\sigma }_z\right)}^2+3·{\left({\alpha }_0·{\tau }_t\right)}^2} \\ {\sigma }_v=\sqrt{{\left(139,09 \frac{N}{mm²}+7,53\frac{N}{mm²}\right)}^2+3·{\left(0,7·8,69\frac{N}{mm²}\right)}^2} \\ {\sigma }_v=147 N/mm² \end{gathered}$$

Die Vergleichsspannung muss geringer sein als

$$\begin{gathered} {\sigma }_{vzul}=\frac{R_{eN}}{S_F} \\ {\sigma }_{vzul}=\frac{300 N}{mm²·1,7} \\ {\sigma }_{vzul}=173,47 \end{gathered}$$

Die Vergleichsspannung ist geringer als die zulässige Vergleichsspannung. Stelle 1 ist also ausreichend dimensioniert.

Stelle 2: zusammengesetzte Beanspruchung aus Zug und Torsion

Zug

${\sigma }_z=\frac{K_A·F}{A}\Rightarrow \frac{K_A·F·4}{\mathrm{\pi }·{\mathrm{d}}^2}$

Werte einsetzen

$$\begin{gathered} {\sigma }_z=\frac{1,25·800 N·4}{\mathrm{\pi }·{12}^2·m{m}^2} \\ {\sigma }_z=8,84 N/mm² \end{gathered}$$

Torsion

$$\begin{gathered} {\tau }_t=\frac{K_A·M_t}{W_t} \Rightarrow \frac{K_A·M_t·16}{\mathrm{\pi }·{\mathrm{d}}^3} \\ {\tau }_t=\frac{1,25·3000 N\cancel{mm}·16}{\mathrm{\pi }·{12}^3 {\mathrm{mm}}^{\cancel{3} 2}} \\ {\tau }_t=11,05 N/mm² \end{gathered}$$

zusammengesetzte Beanspruchung aus Zug, Biegung und Torsion

$$\begin{gathered} {\sigma }_v=\sqrt{{\left({\sigma }_b+{\sigma }_z\right)}^2+3·{\left({\alpha }_0·{\tau }_t\right)}^2} \\ {\sigma }_v=\sqrt{{\left(8,84\frac{N}{mm²}\right)}^2+3·{\left(0,7·11,05\frac{N}{mm²}\right)}^2} \\ {\sigma }_v=16,05 N/mm² \end{gathered}$$

Die Vergleichsspannung ist hier deutlich geringer als die zulässige Vergleichsspannung. Stelle 2 ist also mehr als ausreichend dimensioniert.

Stelle 3: zusammengesetzte Beanspruchung aus Zug und Torsion

Zug

${\sigma }_z=\frac{K_A·F}{A}$

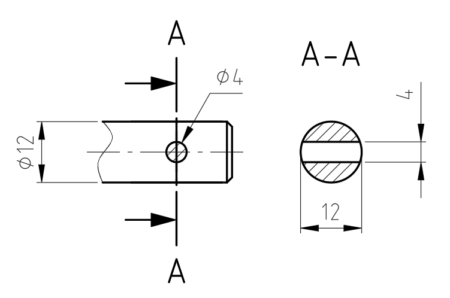
Hier müssen wir bei der Fläche A noch die Bohrung abziehen. Wir sehen die abzuziehende Fläche als Rechteck an. Die Rundung kann aufgrund der Irrelevanz unberücksichtigt bleiben.

$$\begin{gathered} A=\frac{\mathrm{\pi }·{\mathrm{d}}^2}{4}–d_{Stift}·d \\ A=\frac{\mathrm{\pi }·{12}^{2 }{\mathrm{mm}}^2}{4}–4 mm·12 mm \\ A=65,1 mm² \end{gathered}$$

Diese können wir einsetzen.

$$\begin{gathered} {\sigma }_z=\frac{1,25·800 N}{65,1 m{m}^2} \\ {\sigma }_z=15,36 N/mm² \end{gathered}$$

Torsion

Die Formel für W_t bei Zylindern mit zylindrischer bzw. rechteckiger Aussparung finden wir im Roloff Matek TB 11-3

$$\begin{gathered} {\tau }_t=\frac{K_A·M_t}{W_t} \Rightarrow \frac{K_A·M_t}{0,2·D^2·\left(D–1,7·d\right)} \\ {\tau }_t=\frac{1,25·3000 N\cancel{mm}}{0,2·{12}^2 m{m}^2·(12 mm – 1,7 · 4 mm)} \\ {\tau }_t=25,04 N/mm² \end{gathered}$$

zusammengesetzte Beanspruchung aus Zug, Biegung und Torsion

$$\begin{gathered} {\sigma }_v=\sqrt{{\left({\sigma }_b+{\sigma }_z\right)}^2+3·{\left({\alpha }_0·{\tau }_t\right)}^2} \\ {\sigma }_v=\sqrt{{\left(15,36\frac{N}{mm²}\right)}^2+3·{\left(0,7·25,04\frac{N}{mm²}\right)}^2} \\ {\sigma }_v=34,02 N/mm² \end{gathered}$$

Auch hier ist die Vergleichsspannung deutlich geringer als die zulässige Vergleichsspannung. Stelle 3 ist also ebenfalls mehr als ausreichend dimensioniert. Dementsprechend ist Stelle 1 am meisten beanspruchte.

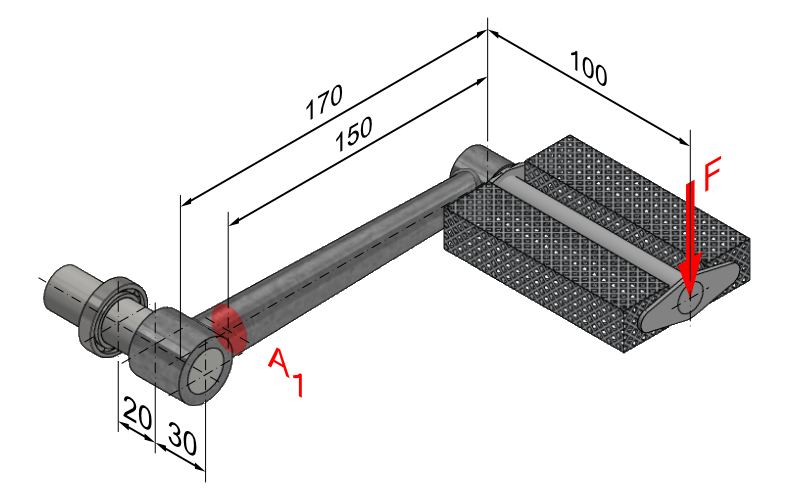
Beispiel 2: Fahrrad Pedal

Wir haben folgende Ausgangssituation.

1. Es soll untersucht werden welchen Durchmesser die Stelle A₁ aufweisen muss, wenn das Pedal für ein Maximalgewicht von 140 kg ausreichend dimensioniert sein soll. Der Werkstoff des Pedals ist E295.
2. Außerdem soll der Wellendurchmesser am Wälzlager bestimmt werden.

Stelle A₁

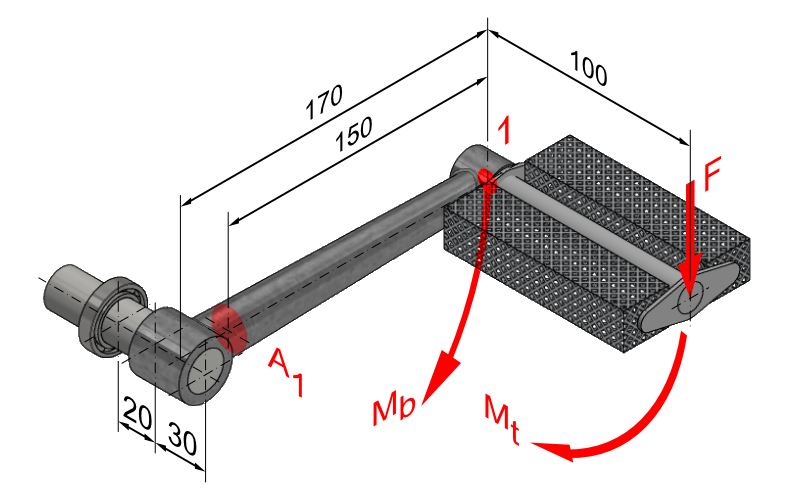
Hier halten wir als erstes fest, dass wenn wir die Kraft auf die Pedale ausüben, die Pedalstange an der Fläche A₁ verdreht werden würde, da zwischen Punkt 1 und der Kraft F aufgrund des 100 mm langen Hebels ein Moment entsteht. Da sich dieses in der Achsrichtung der Fläche A₁ befindet handelt es sich um eine Tangentialspannung, also ein Torsionsmoment M_t.

Außerdem haben wir auch noch eine Biegung, da wir auch lotrecht auf die Fläche A₁ gesehen einen Wirkabstand haben, der durch die Kraft F ein Moment erzeugt. An Punkt 1 haben wir zur Kraft F ein Kräftepaar. Das bedeutet, dass wir am Punkt 1 die selbe Kraft annehmen können wie F, multipliziert man diese mit dem Hebelabstand von 150 mm zur Fläche A, erhalten wir unser Biegemoment M_b.

Reine Zug-, Druck- oder Schubspannung stellen wir nicht fest.

Biegemoment

$M_b=1400 N · 150 mm = 210000 Nmm$

Torsionsmoment

$M_t=1400 N·100 mm=140000 Nmm$

Da wir die Durchmesser ermitteln wollen, diese also noch nicht kennen ermitteln wir nun das Vergleichsmoment M_v. Das Anstrengungsverhältnis ist 1, da Torsion und Biegung den selben Lastfall haben (schwellend).

Vergleichsmoment

$$\begin{gathered} M_v=\sqrt{{M_b}^2+0,75{\left({\alpha }_0·M_t\right)}^2} \\ {M}_v=\sqrt{{(210000 Nmm)}^2+0,75{\left(1·140000 Nmm\right)}^2} \\ {M}_v=242490 Nmm \end{gathered}$$

Anschließend wollen wir den Durchmesser ermitteln. Das Vergleichsmoment wird hierbei gegen das Widerstandsmoment gegen Biegung geprüft. Wir nehmen also die Biegehauptgleichung und stellen diese nach d um.

$$\begin{gathered} {\sigma }_{bzul}=\frac{M_v}{W_b} \\ \overline{){\sigma }_{bzul}=\frac{M_v·32}{\mathrm{\pi }·{\mathrm{d}}^3} }·(\mathrm{\pi }·{\mathrm{d}}^3) \\ \overline{){\mathrm{\sigma }}_{\mathrm{bzul}}·\mathrm{\pi }·{\mathrm{d}}^3={\mathrm{M}}_{\mathrm{v}}·32 }÷({\sigma }_{bzul}·\mathrm{\pi }) \\ \overline{)d^3=\frac{M_v·32}{{\sigma }_{bzul}·\mathrm{\pi }} } \sqrt[3]{} \\ d=\sqrt[3]{\frac{M_v·32}{{\sigma }_{bzul}·\mathrm{\pi }}} \end{gathered}$$

Nun kennen wir alle Werte außer σ_bzul.

${\sigma }_{bzul}=\frac{{\sigma }_{bSchN}}{S_F}=\frac{355 N}{mm²·1,5}=236,67 N/mm²$

Den Wert können wir nun einsetzen.

$$\begin{gathered} d=\sqrt[3]{\frac{M_v·32}{{\sigma }_{bzul}·\mathrm{\pi }}} \\ d=\sqrt[3]{\frac{242490 \cancel{N}mm·32·\cancel{mm²}}{236,67 \cancel{N}·\mathrm{\pi }}} \\ d=21,85 mm \\ {d}_{gew}=22,4 mm (nach DIN 323) \end{gathered}$$

Festigkeitsnachweis

Einen einfachen Festigkeitsnachweis können wir führen indem wir die vorhandene Spannung mit der zulässigen Spannung vergleichen. Die vorhandene Spannung muss kleiner sein.

${\sigma }_{vor} < {\sigma }_{zul}$

Für die vorhandene Spannung haben wir keinen Wert. Wir können diesen jedoch aus dem Vergleichsmoment ableiten.

$$\begin{gathered} {\sigma }_{vorh}=\frac{M_v}{W_b} \\ {\sigma }_{vorh}=\frac{M_v · 32}{\mathrm{\pi }·{\mathrm{d}}^3} \\ {\sigma }_{vorh}=\frac{242490 N\cancel{mm} · 32}{\mathrm{\pi } · 22,4^3 {\mathrm{mm}}^{\cancel{3} 2}} \\ {\sigma }_{vorh}=219,76 N/m{m}^2 < 236,67 N/m{m}^2 \end{gathered}$$

Der Festigkeitsnachweis ist erbracht.

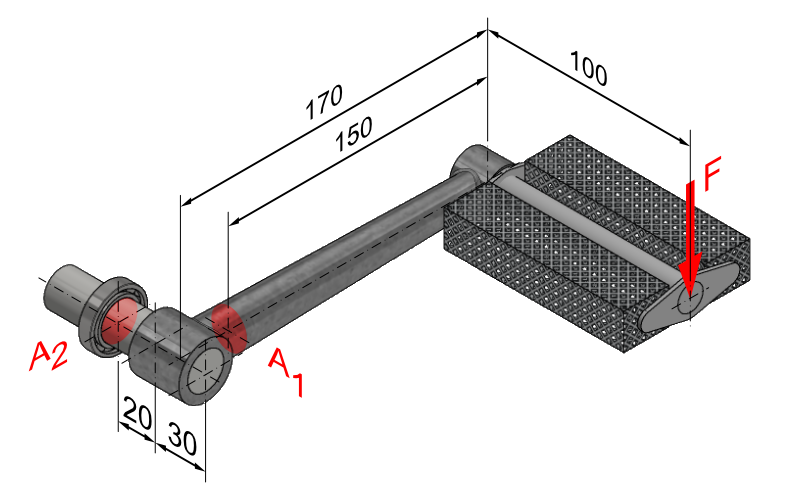
Stelle A₂

Wir untersuchen hier die Stelle A₂ direkt am Wälzlager, da hier der größte Abstand zum Hebel ist und das Biegemoment hier am größten ist. Die Torsion ist hier durch die Pedalstange gegeben, also ähnlich dem Biegemoment von Stelle A₁ nur dieses mal mit einem Hebelarm von 170 mm.

Beim Biegemoment haben wir eine Länge von 35 mm von der Stelle A₁ zur Achse der Pedalstange.

Biegemoment

$M_b=1400 N · 135 mm = 189000 Nmm$

Torsionsmoment

$M_t=1400 N·170 mm=238000 Nmm$

Vergleichsmoment

Hier haben wir jedoch bei der Biegung eine wechselnde Belastung, da die Wellung sich ja um die eigene Achse dreht. Also beträgt das Anstrengungsverhältnis α₀ hier 0,7

$$\begin{gathered} M_v=\sqrt{{M_b}^2+0,75{\left({\alpha }_0·M_t\right)}^2} \\ {M}_v=\sqrt{{(189000 Nmm)}^2+0,75{\left(0,7·238000 Nmm\right)}^2} \\ {M}_v=237780 Nmm \end{gathered}$$

zulässige Biegespannung

${\sigma }_{bzul}=\frac{{\sigma }_{bWN}}{S_F}=\frac{245 N}{mm²·1,5}=163,3\overline{3} N/mm²$

Durchmesser

$$\begin{gathered} d=\sqrt[3]{\frac{M_v·32}{{\sigma }_{bzul}·\mathrm{\pi }}} \\ d=\sqrt[3]{\frac{237780 \cancel{N}mm·32·\cancel{mm²}}{163,3\overline{3} \cancel{N}·\mathrm{\pi }}} \\ d=24,56 mm \\ {d}_{gew}= 25 mm (nach DIN 323) \end{gathered}$$

Festigkeitsnachweis

$$\begin{gathered} {\sigma }_{vorh}=\frac{M_v}{W_b} \\ {\sigma }_{vorh}=\frac{M_v · 32}{\mathrm{\pi }·{\mathrm{d}}^3} \\ {\sigma }_{vorh}=\frac{237,78 N\cancel{mm} · 32}{\mathrm{\pi } · {25}^3 {\mathrm{mm}}^{\cancel{3} 2}} \\ {\sigma }_{vorh}=155,01 N/m{m}^2 < 163,3\overline{3} N/m{m}^2 \end{gathered}$$

Der Festigkeitsnachweis ist erbracht.