Knickung bezeichnet das Knicken eines Objektes bei Beanspruchung auf Druck. Ist die Druckkraft auf ein Objekt zu groß, so kann es knicken. Je länger ein Objekt bei gleichbleibender Querschnittsfläche ist, desto größer ist die Gefahr, dass es knickt. Dabei wird die Knickkraft als jene Kraft bezeichnet, bei der die Knickung des Objektes beginnt. Die Knickspannung ist die Spannung welche im Objekt herrscht, wenn die Knickung beginnt.
Um Knickung zu vermeiden muss demnach die Kraft, die auf das Objekt wirkt geringer sein als die Knickkraft. Übliche Sicherheitsfaktoren gegen Knicken liegen zwischen 3 und 10 (Maschinenbau).
Formelzeichen
| Formelzeichen | Bezeichnung | Einheit |
| Fk | Knickkraft (Kraft bei der die Knickung eintritt) | N |
| Fd | Druckkraft | N |
| l | Länge | mm |
| lk | freie Knicklänge | mm |
| E | Elastizitätsmodul | N/mm² |
| Imin | kleinstes axiales Flächenmoment 2. Grades | mm4 |
| ν | Sicherheitszahl | – |
| λ | Schlankheitsgrad | – |
| λ0 | Grenzschlankheitsgrad | – |
| σk | Knickspannung (Spannung bei der die Knickung eintritt) | N/mm² |
| σd | Druckspannung | N/mm² |
| i | Trägheitsradius | mm |
| S | Querschnittsfläche | mm² |
Formeln
Schlankheitsgrad
Trägheitsradius
zulässige Druckkraft
Druckspannung
zulässige Druckspannung
Sicherheitszahl
Knickspannung (Euler)
Knickkraft (Euler)
Kleinstes axiales Flächenmoment 2. Grades (Euler)
Flächenmoment 2. Grades (kreisförmiger Querschnitt)
Euler-Fall
Bei der Betrachtung auf Knickung nach Euler wird die elastische Knickung behandelt. Also jene Knickung, die nach Wegnahme der Kraft wieder aufgehoben wird und das Objekt in einen Ursprungszustand zurückkehrt.
Euler unterscheidet 4 verschiedene Situationen:
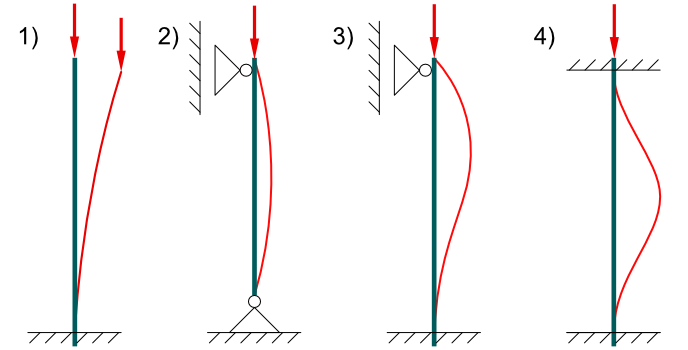
- eingespannt / frei
- Gelenk / Gelenk
- eingespannt / Gelenk
- eingespannt / eingespannt
Die Unterscheidung liegt für die Berechnung in der sogenannten freien Knicklänge lk . Für die 4 unterschiedlichen Situationen werden 4 Faktoren angenommen.
- lk = 2l
- lk = l
- lk = 0,7l
- lk = 0,5l
Die Euler-Gleichung gilt solange wie der errechnete Schlankheitsgrad λ ≥ λ0 beträgt. Wobei die Grenzschlankheitsgrade für die wichtigsten Werkstoffe in Tabellen vorhanden sind. Es folgt ein Auszug.
| Werkstoff | E-Modul E [N/mm²] | Grenzschlankheitsgrad λ0 | Knickspannung nach Tetmajer σk |
| S235 | 210.000 | 105 | σk = 310 – 1,14 · λ |
| E295, E335 | 210.000 | 89 | σk = 335 – 0,62 · λ |
| 5%-Ni-Stahl | 210.000 | 86 | σk = 470 – 2,3 · λ |
| Gusseisen | 100.000 | 80 | σk = 776 – 12 · λ + 0,053 · λ2 |
Tetmajer-Fall
Tetmajer behandelt die plastische Verformung durch Knickung. Da in der Statik eine plastische Verformung unerwünscht ist, werden Bauteile so ausgelegt, dass diese nach Euler bemessen werden können. Die Formeln für die Knickspannung nach Tetmajer resultieren aus Werkstoffprüfungen. (siehe Tabelle oben)
Beispiel
Ein runder Stab aus dem Werkstoff E295 soll eine Kraft von 100 kN mit einer Sicherheit von v = 5 aufnehmen. Die Länge des Stabes beträgt 350 mm. Der Stab ist beidseitig gelagert. Wie groß muss der Durchmesser des Stabes sein?
Lösung:
Zunächst schreiben wir auf was wir wissen.
Werkstoff: E295
Form = rund / kreisförmig
F = 100 kN
v = 5
l = 350 mm
lk = 350 mm (beidseitig gelagert = Euler-Fall 2)
Annahme Euler-Fall
Nun ermitteln wir das kleinste axiale Flächenmoment 2. Grades.
Jetzt können wir diesen Wert nehmen und die Formel zum Flächenmoment 2. Grades nach d umstellen.
anhand dieses Durchmessers können wir jetzt den Schlankheitsgrad λ errechnen.
Nun vergleichen wir den Wert λ mit λ0 und stellen fest, dass λ deutlich kleiner ist. Es liegt also ein Temajer-Fall vor.
Tetmajer-Fall
Wir müssen einen größeren Durchmesser wählen. Da λ deutlich kleiner ist wählen wir einen deutlich größen Durchmesser und legen diesen auf d = 45 mm fest.
Mit dem neu gewählten Durchmesser errechnen wir den Schlankheitsgrad neu. Wobei wir für das Flächenmoment den aus dem Durchmesser resultierenden Wert und nicht Imin nach Euler nehmen müssen!
Anschließend berechnen wir die Knickspannung nach Temajer (siehe Tabelle oben)
Die tatsächliche Druckspannung ermittelt sich durch die Kraft und der Fläche
jetzt schauen wir ob wir den nötigen Sicherheitsfaktor eingehalten haben.
Der Sicherheitsfaktor von 5 ist überschritten. Die Vorgabe somit eingehalten. Wäre der Sicherheitsfaktor kleiner als 5, müssten wir den Durchmesser abermals erhöhen und den Tetmajer Teil erneut mit diesem Durchmesser durchrechnen.
