Zeichnerische / Rechnerische Ermittlung unbekannter Kräfte im zentralen Kräftesystem

Aufgabe

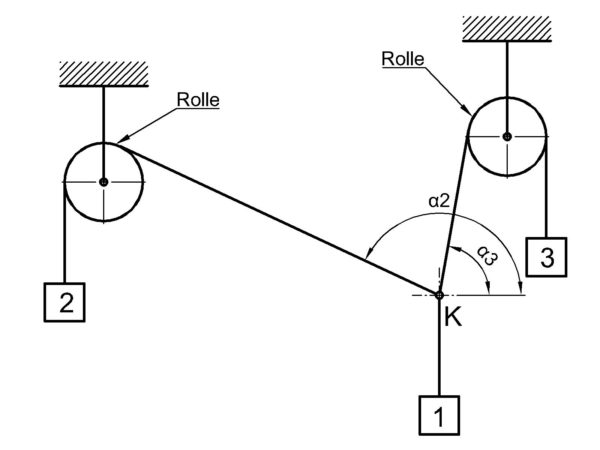
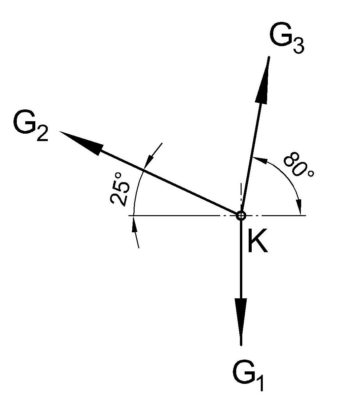
Am Knotenpunkt K sind drei Körper mit Seilen befestigt. Das System ist im Gleichgewicht (Ruhezustand), wenn α₃=80° und α₂=155° ist. Die Gewichtskraft des Körpers 1 beträgt 30 N.

Analytisch und trigonometrisch sind die Gleichungen zur Berechnung der Gewichtskräfte der Körper 2 und 3 zu entwickeln. Wie groß sind die Gewichtskräfte?

Vorgehensweise

System freischneiden / freimachen

Zunächst einmal schneiden wir das System frei um einen besseren Überblick zu erhalten. Die beiden Rollen interessieren uns in diesem Fall nicht, da die Aufgabe nicht vorsieht, die Lagerkräfte zu berechnen die dort herrschen. Die beiden Körper 2 und 3 hängen jeweils an einem Seil, welches über eine lose Rolle liegt. Dieses System wird als reibungsfrei angesehen. Dementsprechend genügt es wenn die Kräfte die vom Knotenpunkt K wegführen eingezeichnet werden, da diese der Gewichtskraft der beiden Körper entsprechen.

Lösungsweg 1 – Zeichnerisch ermitteln

Bei diesem Lösungsansatz zeichnen wir zunächst ein Kräftedreieck in einem vorher definierten Maßstab. In unserem Beispiel beträgt die Kraft G₁ = 30 N. Es bietet sich also an das Dreieck zu vergrößern, da die Messung der Kräfte sonst sehr ungenau wird. Wählen wir z.B. den Maßstab 2:1.

Als erstes legen wir eine Reihenfolge fest in welcher Richtung wir die Kräfte aufzeichnen wollen. Ich entscheide mich in diesem Fall für die Richtung gegen den Uhrzeigersinn, da die Kraft G₁ bekannt ist.
Wir beginnen also mit der bekannten Kraft G₁und zeichnen diese genau wie in der Freischneideskizze senkrecht nach unten, denn genau dies entspricht der Wirklinie der Kraft. Die Länge der Linie beträgt aufgrund des Maßstabes 2:1 – 60 mm.
Nun zeichnen wir vom unteren Punkt der Linie der Kraft G₁ eine Linie unter 80° bezogen auf die horizontale nach oben, ebenfalls wie in der Freischneideskizze zu erkennen.
Vom oberen Punkt der Linie der Kraft G₁ zeichen wir nun die Kraft G₂unter -25° ⁽¹⁾ so ein, dass sich die Linien von G₃und G₂schneiden.
Nun brauchen wir nur noch die Linien der unbekannten Kraftlinien zu messen und durch 2 zu dividieren (Maßstab 2:1).

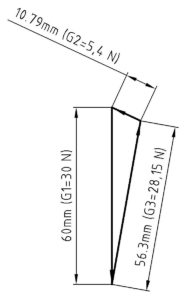
Vielleicht fragt sich der ein oder andere warum -25°? Wir kennen den Betrag der Kraft G₃ nicht, also müssen wir vom oberen Punkt der Linie von G₁ starten. Damit wir also nachher ein geschlossenes Kräftedreieck erhalten, in dem alle Pfeile in die richtige Richtung zeigen, müssen wir den Schnittpunkt von G₂ und G₃ zeichnerisch ermitteln.

Lösungsweg 2 – Sinussatz

Eine weitere Möglichkeit wäre es die Kräfte mit dem Sinussatz (Siehe Winkelfunktionen) zu berechnen. Zunächst zeichnen wir uns wieder ein Dreieck in dem wir die Winkel eintragen und fehlende Winkel anhand der Winkelarten herausfinden. Dieses Dreieck muss nicht maßstäblich sein. Die Winkel habe ich ebenso absichtlich willkürlich eingezeichnet.

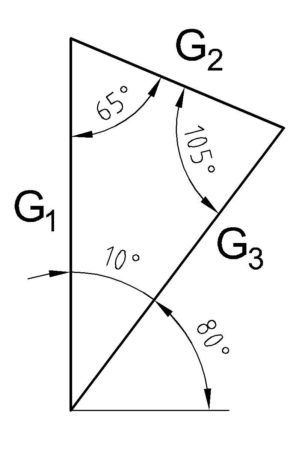
Der Sinussatz für _G3 lautet umgestellt:

$a = \frac{c \cdot \sin α}{\sin γ} = G_{3} = \frac{30 N \cdot \sin (65 °)}{\sin (105 °)} G_{3} = 28, 15 N$

Der Sinussatz für _G2 lautet umgestellt:

$b = \frac{c \cdot \sin β}{\sin γ} = G_{2} = \frac{30 N \cdot \sin (10 °)}{\sin (105 °)} G_{2} = 5, 39 N$

Lösungsweg 3 – Gleichungssystem

Bei dem zentralen Kräftesystem mit drei Kräften ist der Sinussatz die deutlich schnellere Variante. Beim allgemeinen Kräftesystem funktioniert dies jedoch nicht mehr. Deswegen schauen wir uns anhand dieses simplen Beispiels einmal das Gleichungssystem an.

Skizzen anfertigen

Zunächst fertigen wir eine Skizze im X-Y Koordinatensystem an. Ob jede Kraft einzeln rausgezogen wird oder eine einzelne Skizze angefertigt wird ist Geschmackssache. Eine Freischneideskizze benötigen wir ja eh. Bei diesem Schritt wird jede Kraft skizzenhaft in ihre X und Y Komponente zerlegt. Auch diese Skizze muss nicht maßstäblich sein.

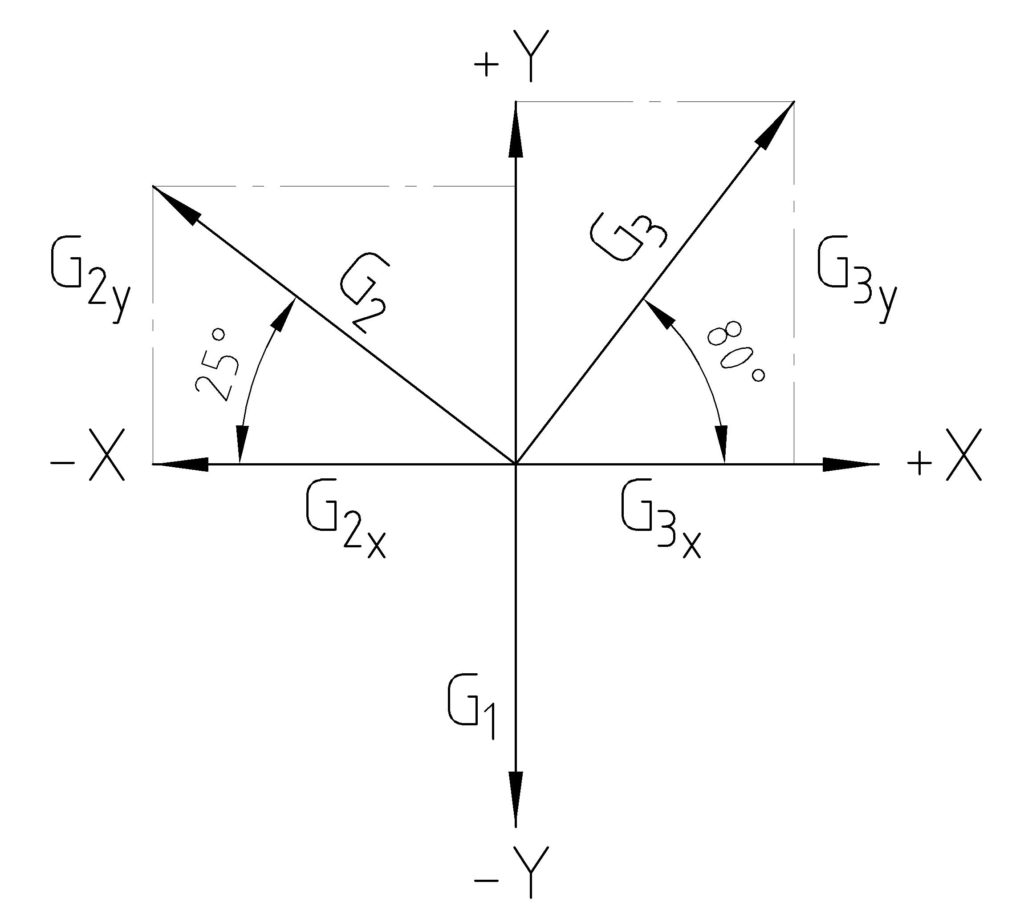
Das X-Y Koordinatenkreuz ist wie gezeigt aufgebaut X Rechts sowie Y oben sind positiv und X links sowie Y unten negativ. Zeichnen wir nun die Kräfte ein, so können wir schnell erkennen ob unsere Kräfte X bzw. Y Komponenten haben und wenn ja ob diese positiv oder negativ sind.

Gleichungen bilden

Das Gleichungssystem ist meistens für alle Kräfte gleich und bildet sich aus dem Grundsatz der Statik, dass das System im Gleichgewicht sein muss. (Siehe: Freiheitsgrade). Das bedeutet, dass die Summe aller Kräfte auf ihrer jeweiligen Achse, sowie die Summe aller Momente 0 sein muss. Die Grundgleichungen lauten also wie folgt.

$Σ F_{X} = 0 Σ F_{Y} = 0 Σ M = 0$

Auf unsere Situation umgesetzt sieht es dann so aus (Kraftmomente sind in diesem Beispiel keine vorhanden) Die Gleichungen werden mit römischen Ziffern durchnummeriert um den Überblick beim Einsetzen nicht zu verlieren.:

$I) Σ F_{X} = 0 = G_{3_{X}} - G_{2_{X}} I I) Σ F_{Y} = 0 = - G_{1} + G_{2_{Y}} + G_{3_{Y}}$

Die X-Komponente von G₃ ist positiv, da G₃ im Koordinatensystem nach rechts zeigt. Die X-Komponente von G₂ ist negativ, da G₂ nach links zeigt. G₁besitzt keine X-Komponente, da der Pfeil senkrecht nach unten zeigt.

Die Y-Komponente von G₁ ist negativ, da der Pfeil nach unten zeigt. Da G₁gar keine X-Komponente besitzt können wir und den Index „Y“ bei der Kraft sparen. Die Y-Komponente von G₂ ist positiv, da der Pfeil nach oben geht. Die Y-Komponente von G3 ist ebenfalls positiv, da auch dieser Pfeil nach oben geht

Einzelgleichungen bilden

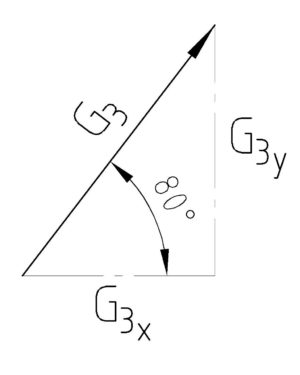
Nun bilden wir die Gleichungen für die Einzelnen Kräfte um diese in die oben gebildeten „Hauptgleichungen“ einzusetzen. Die erste Unbekannte der Gleichung I) ist G_3x also bilden wir die Gleichungen rund um G₃ zuerst. Das kann man aber machen wie man möchte. Wichtig ist nur, dass die Gleichungen nummeriert werden! Schauen wir uns das dazugehörige Dreieck nochmal an.

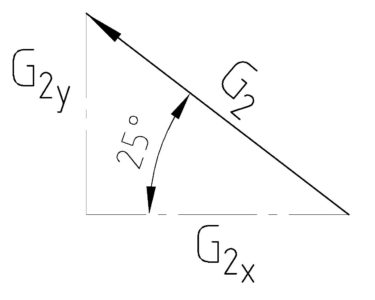
$\sin (α) = \frac{G E G}{H Y P} \sin (80 °) = \frac{G_{3_{Y}}}{G 3} u m s t e l l e n n a c h G_{3_{Y}} I I I) G_{3_{Y}} = \sin (80 °) \cdot G_{3}$ $\cos (α) = \frac{A N K}{H Y P} \cos (80 °) = \frac{G_{3_{X}}}{G 3} u m s t e l l e n n a c h G_{3_{X}} I V) G_{3_{X}} = \cos (80 °) \cdot G_{3}$

Als nächstes bilden wir die Gleichungen um G₂:

$\cos (α) = \frac{A N K}{H Y P} \cos (25 °) = \frac{G_{2_{X}}}{G_{2}} u m s t e l l e n n a c h G_{2_{X}} V) G_{2_{X}} = \cos (25 °) \cdot G_{2}$ $\sin (α) = \frac{G E G}{H Y P} \sin (25 °) = \frac{G_{2_{Y}}}{G_{2}} u m s t e l l e n n a c h G_{2_{Y}} VI) G_{2_{Y}} = \sin (25 °) \cdot G_{2}$

So nun haben wir die Variablen der Hauptgleichungen in einzelne Gleichungen gebildet, sodass wir diese in die Gleichungen einsetzen können:

$I) Σ F_{X} = 0 = G_{3_{X}} - G_{2_{X}} IV) und V) in I) 0 = \cos (80 °) \cdot G_{3} - \cos (25 °) \cdot G_{2}$ $II) Σ F_{Y} = 0 = - G_{1} + G_{2_{Y}} + G_{3_{Y}} VI) und III) in II) VIII) 0 = - G_{1} + \sin (25 °) \cdot G_{2} + \sin (80 °) \cdot G_{3}$

Die untere Gleichung enthält die einzige bekannte Kraft G₁ mit dieser Gleichung rechnen wir weiter. Wir nummerieren diese also mit VIII.

Schauen wir uns die obere Gleichung an. Sie besagt, dass cos(80°) · G₃ – cos(25°)·G₂= 0 ist. Dementsprechend müssen beide resultierende Werte gleich sein. Das bedeutet also.

$G_{2} \cdot \cos (25 °) = G_{3} \cdot \cos (80 °)$

Stellen wir diese Gleichung nach G₂ um. Wir könnten genauso nach G₃umstellen, dass macht absolut keinen Unterschied. Wichtig ist, dass wir uns entscheiden und die Formen dementsprechend einsetzen.

$G_{2} \cdot \cos (25 °) = G_{3} \cdot \cos (80 °) | \div c o s (25 °) V I I) G_{2} = G_{3} \frac{c o s (80 °)}{c o s (25 °)}$

Diese Gleichung können wir nun in die Gleichung VIII einsetzen.

$V I I) i n V I I I) 0 = - G_{1} + \sin (25 °) \cdot (G_{3} \frac{\cos (80 °)}{\cos (25 °)}) + \sin (80 °) \cdot G_{3}$

Stellen wir nun nach G₁ um. Dies ist der einzige Werte den wir kennen.

$0 = - G_{1} + \sin (25 °) \cdot (G_{3} \frac{\cos (80 °)}{\cos (25 °)}) + \sin (80 °) \cdot G_{3} | + G_{1} G_{1} = \sin (25 °) \cdot (G_{3} \frac{\cos (80 °)}{\cos (25 °)}) + \sin (80 °) \cdot G_{3}$

Nun klammern wir G₃aus. Das bedeutet, dass wir alles in Klammern setzen was nicht G₃ ist.

$G_{1} = G_{3} \cdot (\sin (25 °) \cdot (\frac{\cos (80 °)}{\cos (25 °)}) + \sin (80 °))$

Jetzt können wir nach G₃ umstellen indem wir durch die gesamte Klammer dividieren.

$G_{3} = \frac{G_{1}}{\sin (25 °) \cdot (\frac{\cos (80 °)}{\cos (25 °)}) + \sin (80 °)} G_{3} = \frac{30 N}{\sin (25 °) \cdot (\frac{\cos (80 °)}{\cos (25 °)}) + \sin (80 °)} G_{3} = 28, 15 N$

Die Gleichung zur Berechnung von G₂haben wir bereits in der Gleichung VII gebildet.

$VII) G_{2} = G_{3} \cdot \frac{\cos (80 °)}{\cos (25 °)} G_{2} = 28, 15 N \cdot \frac{\cos (80 °)}{\cos (25 °)} G_{2} = 5, 39 N$