Beim Keil ist der Keilwinkel β (der Winkel des Schneidkeils) entscheidend. Dieser wird in Abhängigkeit zur Härte und Festigkeit des zu bearbeitenden Werkstückes gewählt. Dennoch ist durch Reibung entstehnder Verschleiß unausweichlich.
Schneiden mit großem Keilwinkel sind stabiler, während Schneiden mit kleinem Keilwinkel das Trennen erleichtern.
Demnach ist immer der bestmögliche Kompromiss aus Stabilität und Trenneigenschaften zu wählen.
Keilkräfte
Die wirkenden Kräfte am Keil lassen sich sowohl zeichnerisch als auch rechnerisch ermitteln.
Zeichnerisch
Die zeichnerische Ermittlung von wirkenden Kräften am Keil ist denkbar einfach. Man zieht eine Linie rechtwinklig auf die Flanke des Keils. In der gedachten Symmetrieachse des Keils zieht man eine Linie nach unten, dessen Länge einem maßstäblichen Betrag der Kraft entspricht. z.B. 10 N = 10 mm. Die lotrecht auf die Keilflanke zeigende Linie wird um den Mittelpunkt der Kraftlinie gespiegelt. An dem Punk wo sie dich Linien der Raute schneiden bis zu dem Punkt wo sie auf der Mittellinie des Keils trifft kann man die Schneidkraft ablesen. Das Ganze nennt man Kräfteparallelogramm.
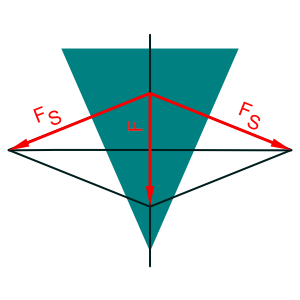
Rechnerisch
Das Kräfteparallelogramm lässt sich natürlich auch rechnerisch umsetzen. Am einfachsten indem man ein Viertel davon betrachtet und ein rechtwinkliges Dreieck erhält, dessen Gegenkathete nun die Hälfte von F ist und die gesuchte Schnittkraft FS die Hypotenuse darstellt. Der spitze Winkel anliegend an FS ist die Hälfte des Keilwinkels β da FS ja rechtwinklig auf den Keil trifft. Somit ergibt sich folgende Formel:
Keilkraft FS berechnen
Keilwinkel berechnen
Kraft F berechnen

Oben sprichst Du von Winkel Alpha, in der Formel von Winkel Beta. Alpha und Beta meinen dasselbe?
Nett wäre den Winkel auch in die Skizze einzuzeichnen.
Einfach zu sehen aus der Formel ist folgendes: Wenn ich bei gegebener, nach unten wirkender Druckkraft F mit Schneidwinkel 1 Grad starte, erhalte ich eine bestimmte, nach außen gerichtete Schneidkraft Fs. Wenn ich nun den Schneidewinkel mehrfach verdopple, halbiert sich jeweils die Schneidkraft Fs. Also eine quadratische Abhängigkeit.
Warum ich dies erwähne?
Stelle Dir ein Radialkugellager vor, z.B. Typ 609. Dieses ist nach Herstellerlisten auch für geringfügig AXIALE Lasten zulässig, aber nicht wird angegeben, wie hoch diese Kraft ist; in der Praxis finde ich genutzte Werte von 20 Prozent.
Das Problem ist: wie kann ich diese Werte rechnerisch quantifizieren, es müssten ÄHNLICHE Kräftediagramme wie hier skizziert, gegeben sein.
Die oben genannte quadratische Abhängigkeit veranlasst mich zu der Aussage, dass Radial-Kugellager mit ERHÖHTER Lagerluft, die zu größeren “Keilwinkeln“ führen – auch wenn Kugellagerkugeln nicht schneiden können – deutlich höhere AXIALE Kräfte erlauben, bevor der maximale elastische Kugel-Deformation, die irreversibel wäre, überschritten wird.
In der Mechanik-Vorlesung habe ich gelernt, dass man die oben aufgestellte Formel nach dem Prinzip der „virtuellen Verrückungen“ herleitet.
Also: die geleistete Arbeit, die man aufwendet, wenn man den Schneidstahl um ein infineteseminales Stück nach unten verschiebt, ist gleich der Arbeit, die man leistet, wenn man seitlich den zu schneidenden Stahl auseinander drückt. Und schon hat man rechtwinklige Dreiecke im Spiel.
Hallo Bastian,
ja du hast recht, hätte ich in der Skizze mit angeben sollen.
auch hast du recht damit, dass Rillenkugellager auch geringe axiale Lasten aufnehmen. Letztendlich hast du bei einem Rillenkugellager keinen typischen Keil, da sich der Winkel durch die Kugelform ständig ändert.
Aber was war überhaupt der Grund der Ausführung in dem Kommentar?