Materialbedarfsplanung

Methoden der Materialbedarfsplanung

Es gibt folgende Methoden in der Materialbedarfsplanung.

Deterministische Materialbedarfsplanung

anhand von Stücklisten, Teileverwendungsnachweisen
Verwendung von Fertigungsprogrammen und Arbeitsplänen
anderen Produktdaten wie z.B. CAD Modellen

Stochastische Bedarfsplanung

anhand von Bedarfsstatistiken / Prognosen
Daten aus der Vergangenheit
analytische Vorhersagemethoden

Heuristische Bedarfsplanung

anhand Schätzungen
keine Ausgangsdaten vorhanden
Primär-, Sekundär- und Tertiärbedarf werden subjektiv geschätzt. z.B. durch Mitarbeiter oder Experten

Materialdisposition

plangesteuerte Bedarfsermittlung

Die plangesteuerte Bedarfsermittlung ist ziemlich genau, aber auch aufwändig und wird somit fast nur für A-Teile benutzt.

Die plangesteuerte Bedarfsermittlung findet an der geplanten Produktionsmenge verkaufsfähiger Enderzeugnisse statt. Dies wird als Primärbedarf bezeichnet. Um Enderzeugnisse zu produzieren und somit den Primärbedarf zu decken werden Komponenten benötigt, dies ist der Bruttosekundärbedarf. Doch dieser muss nicht zwangsläufig jedes Mal komplett bestellt werden, wie die folgende Aufstellung zeigt.

Bruttosekundärbedarf	alle benötigten Komponenten für das Enderzeugnis
+ Zusatzbedarf	evtl. Ausschuss (Erfahrungswert)
= Erweiterter Bruttosekundärbedarf
– Lagerbestand	was schon da ist muss nicht bestellt werden
– Bestellbestand	Mengen die schon im Zulauf sind
+ reservierter Lagerbestand	zuvor reservierter Bestand darf nicht entnommen werden
+ Sicherheitsbestand	eiserne Reserve sollte nur im Notfall angegriffen werden
= Nettosekundärbedarf

Beispiel 1

Ein Kunde bestellt 200 Regale. Ein Regal besteht aus den folgenden Komponenten:

Teil	benötigte Anzahl	Lagerbestand	reservierter Lagerbestand
Rückwand	1	50	–
Seitenteile	2	100	50
Regalbrett	6	100	–
Schrauben	24	2000	–
Schraubenmuttern	24	2000	–

Erfahrungsgemäß fällt 5 % Ausschuss an.

Es ist der Bruttosekundärbedarf und der Nettosekundärbedarf zu ermitteln.

Teil	Bruttosekundärbedarf	Nettosekundärbedarf
Rückwand	210	160
Seitenteile	420	370
Regalbrett	1260	1160
Schrauben	5040	3040
Schraubenmuttern	5040	3040

Beispiel 2

Für folgende Strukturstückliste ist der Sekundärbedarf zu ermitteln. Es werden 200 Stück bestellt.

Stufe		Anzahl	Teilenummer
1	2	Anzahl	Teilenummer
x		1	T1
	x	8	T2
	x	4	T4
x		4	T2
x		8	T3
	x	2	T2
	x	2	T5

Hier ist zunächst darauf zu achten, dass einige Teile in verschiedenen Stufen des Produktes in verschiedener Anzahl vorkommen. Es hilft also, die Struktur zuvor aufzulösen und eine Mengenübersichtsstückliste zu erstellen. (Bruttosekundärbedarf)

Teil	Bruttosekundärbedarf
T1	200
T2	5600
T3	1600
T4	800
T5	3200

Beispiel 3

Es sind 10 Tische bestellt. Es ist der Brutto- und Nettosekundärbedarf zu ermitteln. 10 % Ausschuss werden eingeplant.

Teil	Bezeichnung	Menge
380 120	Tischbein komplett	4
380 121	Stahlrohr	4
380 122	Füße	4
380 123	Stahlring	8
380 200	Arbeitsplatte	1
380 160	Verbindung 1	4
380 161	Verbindung 2	2
380 320	Ablage	1
380 150	Blende komplett	1
380 151	Frontblende	1
380 152	Halterung	4

Aus dem ERP System erhalten wir folgende Daten.

380 152
Sicherheitsbestand	1200
Lagerbestand	24800
Lager Reservierungen	800
Im Zulauf	6000

380 122
Sicherheitsbestand	50
Lagerbestand	360
Lager Reservierungen	60
Im Zulauf	120

380 121
Sicherheitsbestand	50
Lagerbestand	300
Lager Reservierungen	40
Im Zulauf	160

380 123
Sicherheitsbestand	600
Lagerbestand	1800
Lager Reservierungen	100
Im Zulauf	400

Es ist darauf zu achten, dass die Strukturliste zwei Unterbaugruppen enthält, die nicht beschafft werden müssen, da diese aus Einzelkomponenten bestehen. Rechnen wir das mal anhand des Teils 380 121 aus.

Bruttosekundärbedarf	4 · 10 = 40
+ Zusatzbedarf	10 % = 4
= Erweiterter Bruttosekundärbedarf	44
– Lagerbestand	300
– Bestellbestand	160
+ reservierter Lagerbestand	40
+ Sicherheitsbestand	50
= Nettosekundärbedarf	-326

Es sind folglich 326 Stahlrohre 380 121 übrig. Es müssen also keine bestellt werden.

Teil	Bruttosekundärbedarf	Nettosekundärbedarf
380 121	40	-326
380 122	40	-326
380 123	80	-1412
380 200	10	11
380 160	40	44
380 161	20	22
380 320	10	11
380 151	10	11
380 152	40	44

Bei einigen Positionen haben wir keine Daten erhalten. Hier muss also der komplette erweiterte Bruttosekundärbedarf beschafft werden.

Bestellverfahren

Ist der Nettosekundärbedarf ermittelt, gibt es verschiedene Verfahren diesen zu decken.

Bedarfsbezogene Bestellung

Es wird erst dann bestellt, wenn Bedarfe entstehen.
Keine bis wenig Lagerhaltung
Standard für Einzelfertiger
Standard für A-Teile
deterministisch

Terminbezogene Bestellung

Wird auch rhythmisches Bestellverfahren genannt.

benötigte Menge wird regelmäßig in festgelegten Abständen bestellt
Lagerbestand hat keinen direkten Einfluss auf den Zeitpunkt der Bestellung
regelmäßige Bestandsüberprüfungen

Bestandsbezogene Bestellung

Hier wird bezogen auf den Bestand bestellt.

Bestandskontrolle nach jedem Lagerabgang
Bestellung wenn Mindestbestand unterschritten

Ermittlung der optimalen Bestellmenge

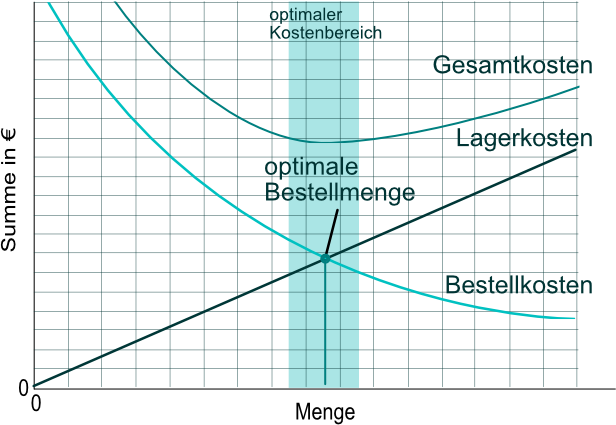
Die optimale Bestellmenge kann aus kostentechnischer Betrachtung anhand der Andler Formel ermittelt werden.

Formelzeichen

Formelzeichen	Bezeichnung	Einheit
x_opt	optimale Losgröße	–
x_ges	Gesamtbedarf pro Lagerung	–
x_B	Bestellmenge	–
n_opt	optimale Bestellhäufigkeit	–
K_R	Rüstkosten	€
k_H	Herstellungskosten pro Teil	€
K_B	fixe Bestellkosten	€
k_f	Planverrechnungskosten pro Teil	€
z_l	Lagerzinssatz pro Teil	%
z_Kb	Zinssatz für Kapitalbildung	%
z_L	Zinssatz für Lagerung	%
Δt_p	optimale Wiederbeschaffungszeit	d, m, y
T_p	Zeitdauer einer Periode	d, m, y
ØB_L	durchschnittlicher Lagerbestand	–
B_S	Sicherheitsbestand	–
W_L	Lagerwert	€
K_L	Lagerhaltungskosten	€

optimale Losgröße zur Lagerung von Eigenfertigungsteilen

$x_{opt}=\sqrt{\frac{200 % \cdot K_{R}\cdot x_{ges}}{k_{H}\cdot z_l}}$

optimale Losgröße zur Lagerung von Fremdbeschaffungsteilen

$x_{opt}=\sqrt{\frac{200 % \cdot K_{B}\cdot x_{ges}}{k_{f}\cdot z_l}}$

Lagerzinssatz pro Teil

$z_{l}=z_{L}+z_{Kb}$

optimale Bestellhäufigkeit

$n_{opt}=\frac{x_{ges}}{x_{opt}}$

optimale Wiederbeschaffungszeit

$\Delta t_{p}=\frac{x_{opt}}{x_{ges}}\cdot T_{p}$

durchschnittlicher Lagerbestand

$\varnothing B_{L}=\frac{x_{B}}{2}+B_{S}$

Lagerwert

$W_{L}= \varnothing B_L\cdot k_{f}$

Lagerhaltungskosten

$K_{L}=W_{L} \cdot z_l$

Beispiel

Ein Bauteil hat einen Bedarf von 480 Stück pro Woche, der Planverrechnungssatz beträgt 8,95 € pro Stück. Der Zinssatz für die Kapitalbildung wurde auf 13 % ermittelt und der Zinssatz für die Lagerhaltung mit 8 % eingepreist. Die festgesetzten Bestellkosten betragen 45 € pro Bestellung.

$x_{opt}=\sqrt{\frac{200 % \cdot 45 \;\euro\cdot 480}{8,95 \;\euro\cdot (13\;% + 8\;%)}}$

$x_{opt}=152$

$n_{opt}=\frac{480}{152}$

$n_{opt}=3,2$

Hier wird von einer 5 Tage Woche ausgegangen.

$\Delta t_{p}=\frac{152}{480}\cdot 5$

$\Delta t_{p}=1,6$

Tabellarische Ermittlung

Durchschnittlicher Lagerbestand

Die optimale Bestellmenge kann auch tabellarisch ermittelt werden. Dazu orientieren wir uns am durchschnittlichen Lagerbedarf und dessen Kosten.

Wird eine Bestellung pro Jahr ausgelöst und der Bestand über ein Jahr wieder abgebaut, so beträgt der durchschnittliche Lagerbestand die Hälfte der Bestellmenge.

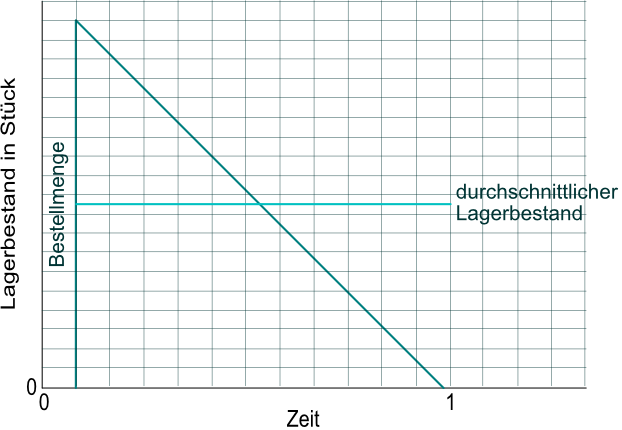
Daran ändert sich auch mit der Häufigkeit der Bestellungen nichts, nur dass das Lager häufiger geleert wird.

$\varnothing B_{L}=\frac{x_{B}}{2}+B_{S}$

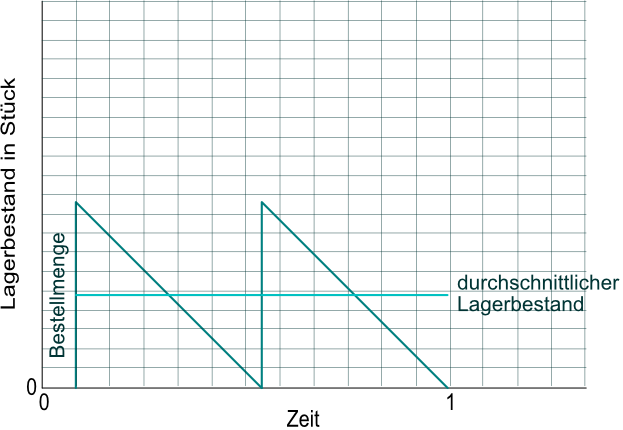
Lagerwert

Der Lagerwert ist das Produkt aus dem durchschnittlichen Lagerbestand und dem Preis pro Stück.

$W_{L}= \varnothing B_L\cdot k_{f}$

Lagerhaltungskosten

Kennen wir den Wert des Lagers, lassen sich daraus die Lagerhaltungskosten ermitteln in dem dieser mit dem Lagerhaltungssatz in % multipliziert wird.

$K_{L}=W_{L} \cdot z_l$

sofern ein Faktor angegeben ist.

$K_{L}=W_{L} \cdot \frac{z_l}{100\;%}$

Beispiel

Es wurden 2400 Teile geliefert. Der Preis pro Stück beträgt 88,5 €. Wir benötigen 800 Stück im Jahr. Die Bestellkosten betragen 150 € und der Lagerhaltungssatz liegt bei 17 %. Es sollen maximal 24 Bestellungen pro Jahr ausgeführt werden.

Anzahl Bestellungen in €	Bestellmenge in Stück (x_ges)	durschn. Lagerbestand in Stück (ØB_L)	Lagerwert in € (W_L)	Lagerhaltungskosten in € (K_L)	Bestellkosten in € (K_B)	Gesamtkosten in € (K_G)
1	2400	1200	106.200,00 €	18.054,00 €	150,00 €	18.204,00 €
2	1200	600	53.100,00 €	9.027,00 €	300,00 €	9.327,00 €
4	600	300	26.550,00 €	4.513,50 €	600,00 €	5.113,50 €
6	400	200	17.700,00 €	3.009,00 €	900,00 €	3.909,00 €
12	200	100	8.850,00 €	1.504,50 €	1.800,00 €	3.304,50 €
18	133,3333333	66,66666667	5.900,00 €	1.003,00 €	2.700,00 €	3.703,00 €
24	100	50	4.425,00 €	752,25 €	3.600,00 €	4.352,25 €

Die optimale Bestellmenge beträgt also bei 12 Bestellungen. Also ca. 200 Stück

Materialbedarfsplanung

Methoden der Materialbedarfsplanung

Deterministische Materialbedarfsplanung

Stochastische Bedarfsplanung

Heuristische Bedarfsplanung

Materialdisposition

plangesteuerte Bedarfsermittlung

Beispiel 1

Beispiel 2

Beispiel 3

Bestellverfahren

Bedarfsbezogene Bestellung

Terminbezogene Bestellung

Bestandsbezogene Bestellung

Ermittlung der optimalen Bestellmenge

Beispiel

Tabellarische Ermittlung

Beispiel

Nils

Schreibe einen KommentarAntworten abbrechen