Die Break-Even Analyse dient dazu, zu ermitteln, ab welcher Absatzmenge ein Produkt Gewinn erwirtschaftet. Dies funktioniert ähnlich wie die Ermittlung der kritischen Menge bei der Make or Buy Analyse. Der Punkt an dem die Kosten gedeckt aber noch kein Gewinn erwirtschaftet wird, nennt sich Break-Even-Point. Dieser Punkt wird auch Gewinnschwelle genannt. Jeder Absatz oberhalb dieses Punkts erwirtschaftet demnach Gewinn.
Beispiel
Ein Produkt hat fixe Kosten von 595.000,00 € pro Jahr und variable Stückkosten von 2o5,00 €. Es wird ein Listenverkaufspreis von 290,00 € angestrebt die Absatzprognose beträgt 10.000 Stück und die Kapazitätsgrenze liegt bei 13.000 Stück
Tabellarische Ermittlung
| Absatzmenge | fixe Kosten | variable Kosten | variable Kosten | Gesamtkosten | Umsatz | Umsatzerlöse | Gewinn / Verlust |
| [Stück] | (gesamt) [€] | pro Stück [€] | (gesamt) [€] | [€] | pro Stück [€] | (gesamt) [€] | [€] |
| 3000 | 595.000,00 | 205,00 | 615.000,00 | 1.210.000,00 | 290,00 | 870.000,00 | -340.000,00 |
| 4000 | 595.000,00 | 205,00 | 820.000,00 | 1.415.000,00 | 290,00 | 1.160.000,00 | -255.000,00 |
| 5000 | 595.000,00 | 205,00 | 1.025.000,00 | 1.620.000,00 | 290,00 | 1.450.000,00 | -170.000,00 |
| 6000 | 595.000,00 | 205,00 | 1.230.000,00 | 1.825.000,00 | 290,00 | 1.740.000,00 | -85.000,00 |
| 7000 | 595.000,00 | 205,00 | 1.435.000,00 | 2.030.000,00 | 290,00 | 2.030.000,00 | 0,00 |
| 8000 | 595.000,00 | 205,00 | 1.640.000,00 | 2.235.000,00 | 290,00 | 2.320.000,00 | 85.000,00 |
| 9000 | 595.000,00 | 205,00 | 1.845.000,00 | 2.440.000,00 | 290,00 | 2.610.000,00 | 170.000,00 |
| 10000 | 595.000,00 | 205,00 | 2.050.000,00 | 2.645.000,00 | 290,00 | 2.900.000,00 | 255.000,00 |
| 11000 | 595.000,00 | 205,00 | 2.255.000,00 | 2.850.000,00 | 290,00 | 3.190.000,00 | 340.000,00 |
| 12000 | 595.000,00 | 205,00 | 2.460.000,00 | 3.055.000,00 | 290,00 | 3.480.000,00 | 425.000,00 |
| 13000 | 595.000,00 | 205,00 | 2.665.000,00 | 3.260.000,00 | 290,00 | 3.770.000,00 | 510.000,00 |
Nun sieht man schon, dass der Break-Even-Point bei 7000 Stück liegt.
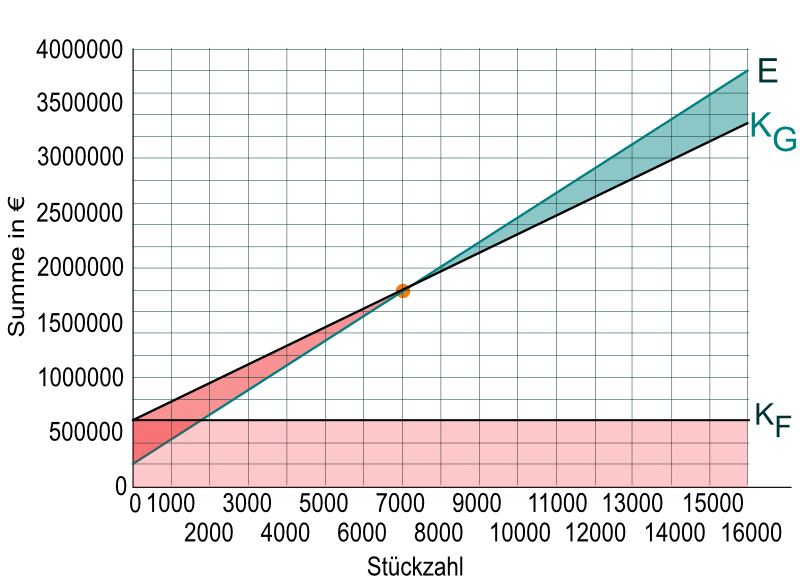
Grafische Ermittlung
Wir starten bei 3000 Stück mit der Kostenlinie auf 1210.000,00 € und enden bei bei 13000 Stück mit 3.260.000,00 €. Bei der Erlöslinie gehen wir ebenso vor.
Der Break-Even-Point ist der Schnittpunkt der beiden Geraden. Der Bereich unterhalb der Erlösline und oberhalb der Kostenlinie kennzeichnet den Gewinn. Unterhalb der Kostenline und oberhalb der Erlöslinie stellt den Verlustbereich dar.
Rechnerische Ermittlung
Die grafische Ermittlung ist unter Umständen ungenau und außerdem recht aufwendig. doch man kann den Break-Even-Point auch rechnerisch ermitteln.
Formelzeichen
| Formelzeichen | Beschreibung | Einheit |
| KG | Gesamtkosten | € |
| KF | Fixkosten | € |
| KV | variable Kosten | € |
| kf | fixe Kosten pro Stück | € |
| kv | variable Kosten pro Stück | € |
| p | Verkaufspreis pro Stück | € |
| x | Absatzmenge | Stück |
Gesamtkosten
Zunächst einmal überlegen wir uns wie sich die Gesamtkosten KG ermitteln lassen. Diese beinhalten sowohl die gesamten fixen Kosten, sowie die variablen Kosten.
KG = KF + kv · x
Erlös
Der Erlös ist das Produkt aus dem Verkaufspreis pro Stück und der Absatzmenge
E = p · x
Break-Even-Point
Der Break-Even-Point ist der Punkt an dem Erlös und Gesamtkosten gleich groß sind. Wir setzen also gleich.
E = KG
Diese Gleichung können wir nach x umstellen. Indem wir x zunächst auf die andere Seite holen und anschließend ausklammern.
Setzen wir die Werte ein und überprüfen das Ergebnis.