Optimierung der Fertigung

Die Optimierung der Fertigung kann wesentlich zur besseren Wirtschaftlichkeit beitragen. In diesem Beispiel möchte eine Firma die Fertigung einer Baugruppe mittels Fließprinzip über CNC Maschinen und einem einzelnen Bearbeitungszentrum (BAZ) abwickeln. Die Montage findet an Handarbeitsplätzen statt. Die Auflage soll 15.000 Stück zu 750 €/Stück betragen. Unsere Aufgabe soll es sein die Rüstzeiten zu optimieren. Folgende Einzelzeiten wurden für die jeweiligen Arbeitsgänge gemessen.

Optimierung der Fertigung – Rüstzeiten

Pos.	Arbeitsgang				BAZ	CNC	Bedarf
	1	2	3	4	tr [min]	tr [min]	Lose / a


1	Drehen				40	20	45
		Fräsen				20
			Bohren			10
				Schleifen		20
2	Bohren				50	20	90
		Drehen				30
			Härten			30
				Schleifen		10
3	Drehen				60	30	80
		Bohren				20
			Fräsen			30
				Schleifen		40
4	Bohren				60	20	60
		Fräsen				30
			Drehen			50
				Härten		50
5	Bohren				60	20	40
		Drehen				20
			Fräsen			40
				Härten		50

Vergleich der Rüstzeiten

Zunächst einmal müssen wir die Zeiten in ein vergleichbares Format bringen. Dazu vergleichen wir für jedes Bauteil und die Anzahl dessen Lose die Rüstzeiten des Bearbeitungszentrums mit der Summe der Einzel-Rüstzeiten der CNC Maschinen.

	Lose	Σ tr CNC	tr BAZ	Rüstzeit Differenz
Bauteil 1	45	3150	1800	1350
Bauteil 2	90	8100	4500	3600
Bauteil 3	80	9600	4800	4800
Bauteil 4	60	9000	3600	5400
Bauteil 5	40	5200	2400	2800

Wir stellen fest, dass die Differenz der Rüstzeiten beim Bauteil 4 am höchsten ist. Hier macht es also Sinn dieses Bauteil am einzigen zur Verfügung stehenden BAZ zu bearbeiten. Diese Zeile streichen wir durch. Diese brauchen wir bei weiteren Optimierungen nicht mehr berücksichtigen.

	Lose	Σ tr CNC	tr BAZ	Rüstzeit Differenz
Bauteil 1	45	3150	1800	1350
Bauteil 2	90	8100	4500	3600
Bauteil 3	80	9600	4800	4800
~~Bauteil 4~~	60	~~9000~~	~~3600~~	~~5400~~
Bauteil 5	40	5200	2400	2800

Materialflussmatrix aufstellen

Die Materialflussmatrix wird bei der Fließfertigung genutzt, um den sogenannten Linearitätsgrad zu bestimmen. In der Fließfertigung soll das Werkstück möglichst nicht wieder rückwärtslaufen. Umso höher der Linearitätsgrad, desto besser ist es. Wir stellen die Matrix so auf, dass wir sowohl in den Spalten als auch in den Zeilen dieselbe Reihenfolge haben.

Verglichen werden hier der Bedarf in Lose, also die Stückzahlen, die durch die Fertigung laufen. Jeweils in der Abfolge, wie sie geplant waren. Da in keinem Fall ein Arbeitsschritt zwei Mal ausgeführt wird, können wir alle „Paare“ schon mal streichen.

	Drehen	Fräsen	Bohren	Sägen	Härten
Drehen	–	85	80	0	90
Fräsen	0	–	45	80	40
Bohren	130	80	–	45	0
Schleifen	0	0	0	–	0
Härten	0	0	0	90	–

Linearitätsgrad bestimmen

Da wir die Tabelle von Links nach rechts in die Tabelle eintragen, bedeutet es, dass alle Lose oberhalb der Striche Hinbewegungen sind und alle unterhalb Rückbewegungen.

$L=\frac{\sum Hinbew.}{\sum \left ( Hinbew. + Rueckbew. \right )} \cdot 100%$

$L=\frac{465}{\sum \left ( 465 + 300 \right )} \cdot 100%$

$L=60,78 %$

Quotientenvergleich

Anschließend machen wir für jeden Arbeitsschritt den Quotitentenvergleich. Den Arbeitsgang mit dem höchsten Wert setzen wir an erster Stelle.

	Drehen	Fräsen	Bohren	Schleifen	Härten	Σ
Drehen	–	85	80	0	90	255
Fräsen	0	–	45	80	40	165
Bohren	130	80	–	45	0	255
Schleifen	0	0	0	–	0	0
Härten	0	0	0	90	–	90
Σ	130	165	125	215	130	–

$Q_{D}=\frac{255}{130}=1,96$

$Q_{F}=\frac{165}{165}=1$

$Q_{B}=\frac{255}{125}=2,04$

$Q_{S}=\frac{0}{215}=0$

$Q_{H}=\frac{90}{130}=0,69$

In diesem Fall ist also das Bohren der erste Arbeitsschritt und fällt somit aus der nächsten Matrix weg.

	Drehen	Fräsen	Schleifen	Härten	Σ
Drehen	–	85	0	90	175
Fräsen	0	–	80	40	130
Schleifen	0	0	–	0	0
Härten	0	0	90	–	90
Σ	0	85	170	130	–

$Q_{D}=\frac{175}{0}=\infty$

Hier haben wir einen nahezu unendlich großen Wert, weswegen wir diesen automatisch als den höchsten ansehen können. Der zweite Arbeitsschritt ist also das Drehen.

	Fräsen	Schleifen	Härten	Σ
Fräsen	–	80	40	120
Schleifen	0	–	0	0
Härten	0	90	–	90
Σ	0	170	40	–

$Q_{F}=\frac{120}{0}=\infty$

Hier dasselbe, der nächste Arbeitsschritt ist also Fräsen.

	Schleifen	Härten	Σ
Schleifen	–	0	0
Härten	90	–	90
Σ	90	0	–

$Q_{S}=\frac{0}{90}=0$

$Q_{H}=\frac{90}{0}=\infty$

Unendlich ist größer als 0, der nächste Arbeitsschritt ist also Härten.

Zum Schluss bleibt also nur noch Schleifen übrig.

Die optimierte Reihenfolge ist also Bohren → Drehen → Fräsen → Härten → Schleifen

Vergleich der Nebenzeiten

Die Nebenzeiten zu vergleichen ist ein weiterer Schritt zur Optimierung der Fertigung. Zur Ermittlung der Nebenzeiten kann es sinnvoll sein sich eine Tabelle anzufertigen, um diese übersichtlich darzustellen. In diesem Beispiel gehen wir davon aus, dass die Anzahl der Transporte, die Transportzeit pro Los und die Liegezeiten bekannt sind.

Fließfertigung
Item	Lose/a	Anzahl der Transporte	Transportzeit		Anzahl der Umsteuervorgänge	Liegezeit		Nebenzeit
Item	Lose/a	Anzahl der Transporte	T_Tin h	Ʃ T_Tin h	Anzahl der Umsteuervorgänge	T_L in h	Ʃ T_Lin h	Ʃ T_T + Ʃ T_Lin h
Pos. 1 Antriebspindel		3	0,5			0,5
Pos. 2 Spindelbuchse		3	0,5			0,5
Pos. 3 Gehäusedeckel		3	0,5			0,5
Pos. 5 Stahlgehäuse		3	0,5			0,5
Gesamte Nebenzeit der Fließfertigung in Stunden:
Werkstättenfertigung
Item	Lose/a	Anzahl der Transporte	Transportzeit T_Tpro Auftrag in h		Transportzeit aller Lose Ʃ T_T in h
Pos.1 Antriebspindel		3	1
Pos.2 Spindelbuchse		3	1
Pos.3 Gehäusedeckel		3	1
Pos. 5 Stahlgehäuse		3	1
Gesamte Nebenzeit der Werkstättenfertigung in Stunden:

Transportzeiten

Als erstes übertragen wir die Anzahl der Lose der Bauteile ein. Damit können wir schon mal die Summe der Transportzeiten Σ T_T ermitteln. Diese ist das Produkt aus der Anzahl der Lose, Anzahl der Transporte und der Einzeltransportzeit T_T

$\Sigma \; T_{T} = Lose/a \cdot Anz. Transp. \cdot T_{T}$

Fließfertigung
Item	Lose/a	Anzahl der Transporte	Transportzeit		Anzahl der Umsteuervorgänge	Liegezeit		Nebenzeit
Item	Lose/a	Anzahl der Transporte	T_Tin h	Ʃ T_Tin h	Anzahl der Umsteuervorgänge	T_L in h	Ʃ T_Lin h	Ʃ T_T + Ʃ T_Lin h
Pos.1 Antriebspindel	45	3	0,5	67,5		0,5
Pos.2 Spindelbuchse	90	3	0,5	135		0,5
Pos.3 Gehäusedeckel	80	3	0,5	120		0,5
Pos.5 Stahlgehäuse	40	3	0,5	60		0,5
Gesamte Nebenzeit der Fließfertigung in Stunden:
Werkstättenfertigung
Item	Lose/a	Anzahl der Transporte	Transportzeit T_Tpro Auftrag in h		Transportzeit aller Lose Ʃ T_T in h
Pos.1 Antriebspindel	45	3	1		135
Pos.2 Spindelbuchse	90	3	1		270
Pos.3 Gehäusedeckel	80	3	1		240
Pos.5 Stahlgehäuse	40	3	1		120
Gesamte Nebenzeit der Werkstättenfertigung in Stunden:					765

Umsteuervorgänge

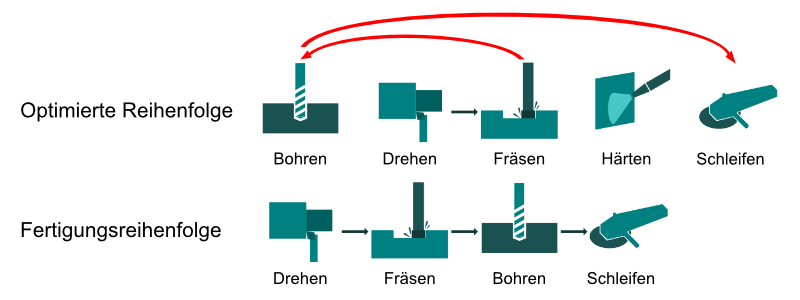
Von einem Umsteuervorgang spricht man immer dann, wenn bei der Fließfertigung ein Arbeitsschritt nicht in der vorgesehenen Reihenfolge stattfinden kann. Dazu vergleichen wir die optimierte Reihenfolge der Fließfertigung mit den Arbeitsschritten, die zur Fertigung des Bauteils notwendig sein. Die dunkelgrünen Pfeile stellen die „normale“ Bearbeitungsreihenfolge dar, während die roten Pfeile die Umsteuervorgänge anzeigen.

Pos.1 Arbeitsspindel

Die Arbeitsspindel wird zunächst gedreht, dann gefräst, gebohrt und anschließend geschliffen. Die optimierte Fertigungsstraße ist nun aber anders aufgebaut. Wir müssen nun schauen, wie viele Umsteuervorgänge stattfinden. Also all die Vorgänge, wo ein Arbeitsschritt übersprungen wird, oder eine Rückwärtsbewegung durchgeführt wird.

Hier liegen also zwei Umsteuervorgänge vor.

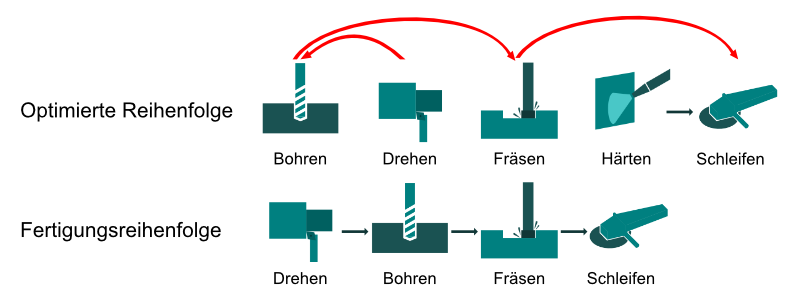
Pos.2 Spindelbuchse

Hier haben wir einen Umsteuervorgang

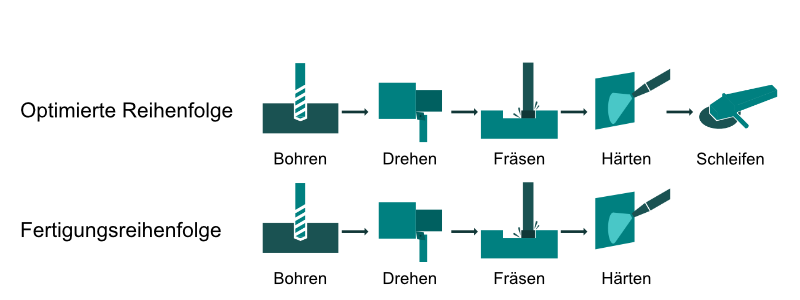
Pos.3 Gehäusedeckel

Beim Gehäusedeckel gibt es 3 Umsteuervorgänge

Pos.5 Stalgehäuse

Das Stahlgehäuse kommt ganz ohne Umsteuervorgänge aus.

Die Summe der Liegezeiten Σ T_List das Produkt aus der Anzahl der Lose, der Einzelliegezeit T_Lund der Anzahl der Umsteuervorgänge.

$\Sigma = Lose/a \cdot Anz. Umsteuerv. \; \cdot T_{L}$

Fließfertigung
Item	Lose/a	Anzahl der Transporte	Transportzeit		Anzahl der Umsteuervorgänge	Liegezeit		Nebenzeit
Item	Lose/a	Anzahl der Transporte	T_Tin h	Ʃ T_Tin h	Anzahl der Umsteuervorgänge	T_L in h	Ʃ T_Lin h	Ʃ T_T + Ʃ T_Lin h
Pos.1 Antriebspindel	45	3	0,5	67,5	2	0,5	45	112,5
Pos.2 Spindelbuchse	90	3	0,5	135	1	0,5	45	180
Pos.3 Gehäusedeckel	80	3	0,5	120	3	0,5	120	240
Pos.5 Stahlgehäuse	40	3	0,5	60	0	0,5	0	60
Gesamte Nebenzeit der Fließfertigung in Stunden:								592,5
Werkstättenfertigung
Item	Lose/a	Anzahl der Transporte	Transportzeit T_Tpro Auftrag in h		Transportzeit aller Lose Ʃ T_T in h
Pos.1 Antriebspindel	45	3	1		135
Pos.2 Spindelbuchse	90	3	1		270
Pos.3 Gehäusedeckel	80	3	1		240
Pos.5 Stahlgehäuse	40	3	1		120
Gesamte Nebenzeit der Werkstättenfertigung in Stunden:					765

Durch die Umstellung auf die Fließfertigung spart man 172,5 h Nebenzeiten im Jahr, somit werden die Produktionskosten geringer.